高中数学人教版新课标B选修2-12.2 椭圆课文内容ppt课件

这是一份高中数学人教版新课标B选修2-12.2 椭圆课文内容ppt课件，共18页。PPT课件主要包含了生活中的椭圆，一问题情境，复习回顾，学生活动，坐标法，方案一，椭圆的标准方程，abc之间的关系，c2a2-b2等内容，欢迎下载使用。

如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢？
♦ 动画演示：“神六”飞行
注意:椭圆定义中容易遗漏的三处地方： （1） 必须在平面内. （2）两个定点---两点间距离确定． （3）绳长--轨迹上任意点到两定点距离和确定．思考：在同样的绳长下，两定点间距离较长，则所画出的椭圆较扁（　　线段）在同样的绳长下，两定点间距离较短，则所画出的椭圆较圆（　　圆）由此可知，椭圆的形状与两定点间距离、绳长有关．
PF1+PF2=2a (2a>2c>0, F1F2=2c)
设圆上任意一点P(x，y)
以圆心O为原点，建立直角坐标系
两边平方，得
♦ 回忆在必修2中是如何求圆的方程的？
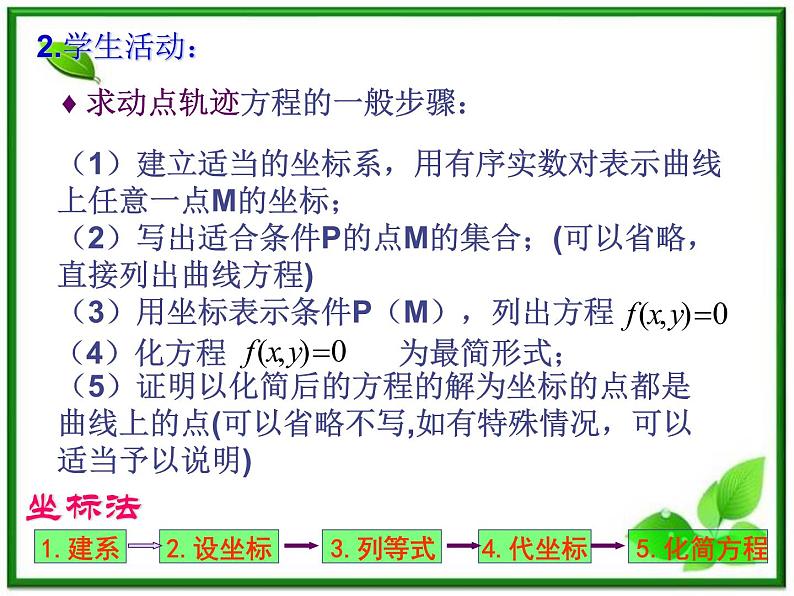
♦ 求动点轨迹方程的一般步骤：
（1）建立适当的坐标系，用有序实数对表示曲线上任意一点M的坐标；（2）写出适合条件P的点M的集合；(可以省略，直接列出曲线方程)（3）用坐标表示条件P（M），列出方程 （5）证明以化简后的方程的解为坐标的点都是曲线上的点(可以省略不写,如有特殊情况，可以适当予以说明)
（4）化方程 为最简形式；
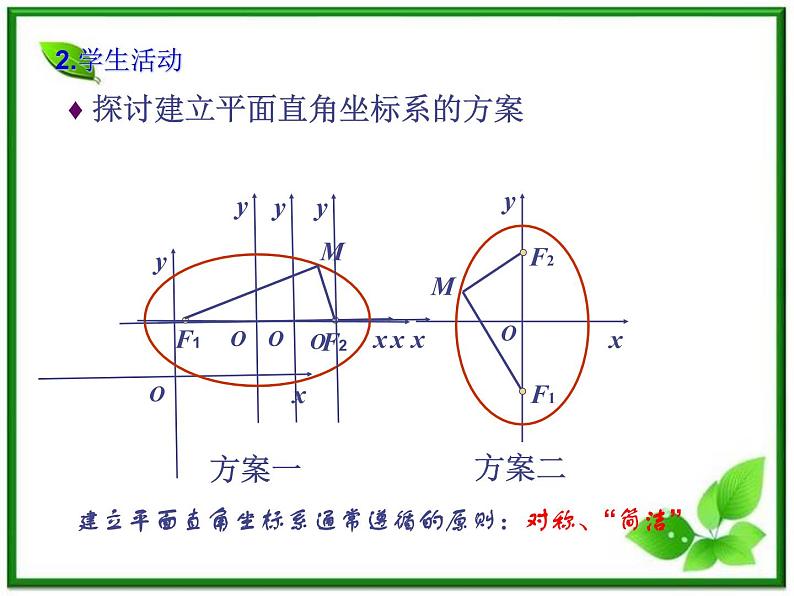
♦ 探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则：对称、“简洁”
解：取过焦点F1、F2的直线为x轴，线段F1F2的垂直平分线为y轴，建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点，椭圆的焦距2c(c>0)，M与F1和F2的距离的和等于正常数2a (2a>2c) ，则F1、F2的坐标分别是(c,0)、(c,0) .
（问题：下面怎样化简？）
由椭圆的定义得，限制条件：
1)椭圆的标准方程的推导
总体印象：对称、简洁，“像”直线方程的截距式
MF1+MF2=2a (2a>2c>0)
3)两类标准方程的对照表
共同点：椭圆的标准方程表示的一定是焦点在坐标轴上，中心在坐标原点的椭圆；方程的左边是平方和，右边是1.
例1 ： 已知一个运油车上的贮油罐横截面的外轮廓线是一 个椭圆， 它的焦距为2.4m，外轮廓线上的点到两个焦点距离的和为 3m，求这个椭圆的标准方程．
以两焦点F1、F2所在直线为x轴，线段F1F2的垂直平分线为 y 轴，建立如图所示的直角坐标系xOy，则这个椭圆的标准方程可设为
因此，这个椭圆的标准方程为
(-3,0)、(3,0)
1.口答：下列方程哪些表示椭圆？
例2 ：将圆 = 4上的点的横坐标保持不变，纵坐标变为原来的一半，求所的曲线的方程，并说明它是什么曲线？
1）将圆按照某个方向均匀地压缩（拉长），可以得到椭圆。2）利用中间变量求点的轨迹方程的方法是解析几何中常用的方法；
例3、写出适合下列条件的椭圆的标准方程
(1) a =4，b=1，焦点在 x 轴上； (2) a =4，b=1，焦点在坐标轴上； (3) 两个焦点的坐标是（ 0 ，-2）和（ 0 ，2），并且经 过点P（ -1.5 ，2.5）.
解： 因为椭圆的焦点在y轴上， 设它的标准方程为
∵ c=2，且 c2= a2 - b2
∴ 4= a2 - b2 ……①
(法二) 因为椭圆的焦点在y轴上，所以设它的标准方程为
所以所求椭圆的标准方程为