






2020-2021学年一 平行线等分线段定理教案配套ppt课件
展开1.理解平行线等分线段定理及推论.2.掌握任意等分线段的方法3. 能利用平行线等分线段定理解决简单几何问题.
1.平行线等分线段定理:如果一组________在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.2.推论1:经过三角形一边的中点与另一边平行的直线必________第三边.3.推论2:经过梯形一腰的中点,且与底边平行的直线________另一腰.
1.平行线2.平分3.平分
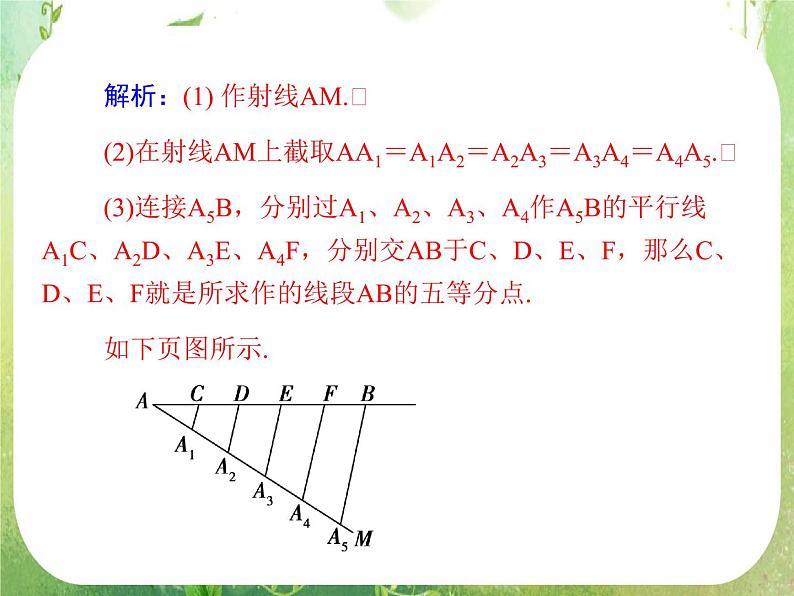
已知线段AB,求作AB的五等分点.
分析:本题是平行线等分线段定理的实际应用.只要作射线AM,在AM上任意截取5条相等线段,连接最后一等分的后端点A5与点B,再过其他分点作BA5的平行线,分别交AB于C、D、E、F,则AB就被这些平行线分成五等分了.
解析:(1) 作射线AM.(2)在射线AM上截取AA1=A1A2=A2A3=A3A4=A4A5.(3)连接A5B,分别过A1、A2、A3、A4作A5B的平行线A1C、A2D、A3E、A4F,分别交AB于C、D、E、F,那么C、D、E、F就是所求作的线段AB的五等分点.如下页图所示.
已知:如图所示,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F.求证:AF= AC.
证明:如图,过点D作DG∥BF交AC于点G.
在△BCF中,D是BC的中点,DG∥BF,∴G为CF的中点,即CG=GF.在△ADG中,E是AD的中点,BF∥DG,∴F是AG的中点,即AF=FG.∴AF= AC.点评:构造基本图形法是重要的数学思想方法.
如图所示,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,BA、CD的延长线分别与EF的延长线交于点M、N.求证:∠AME=∠CNE.
证明:如图,连接BD,取BD的中点G,连接GE、GF.在△ABD中,∵点G、F分别是BD、AD的中点,∴GF= AB,GF∥BM.同理可证:GE= CD,GE∥CN.∵AB=CD,∴GF=GE.∴∠GEF=∠GFE.∵GF∥BM,∴∠GFE=∠BME.∵GE∥CD,∴∠GEF=∠CNE.∴∠AME=∠CNE.
1.下列用平行线等分线段的图形中,错误的是( )
2.如图所示,l1∥l2∥l3,直线AB与l1、l2、l3相交于点A、E、B,直线CD与l1、l2、l3相交于点C、E、D,AE=EB,则有( )A.AE=CE B.BE=DEC.CE=DE D.CE>DE
3.如图所示,AB∥CD∥EF,且AO=OD=DF,BC=6,则BE为( )A.9 B.10C.11 D.12
4.AD是△ABC的高, ,M,N在AB上,且AM=MN=NB,ME⊥BC于E,NF⊥BC于F,则FC=( )A. B. C. D.
5.在梯形ABCD中,M、N分别是腰AB与腰CD的中点,且AD=2,BC=4,则MN等于( )A.2.5 B.3C.3.5 D.不确定
6.如图所示,已知a∥b∥c,直线m、n分别与直线a、b、c交于点A、B、C和点A′、B′、C′,如果AB=BC=1,A′B′= ,则B′C′=______.
7.顺次连接梯形各边中点连线所围成的四边形是__________.
8.如图所示,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD= ,点E、F分别为线段AB、AD的中点,则EF=____.
解析:连接DE,由于E是AB的中点,故BE= .又CD= ,AB∥DC,CB⊥AB,∴四边形EBCD是矩形.在Rt△ADE中,AD=a,F是AD的中点,故EF= .答案:
9.如下图所示,已知AD∥EF∥BC,E是AB的中点,则DG=____,点H是______的中点,点F是______的中点.
答案:BG AC CD
10.如图所示,AB=AC,AD⊥BC于点D,M是AD的中点,CM交AB于点P,DN∥CP.若AB=6 cm,则AP=____;若PM=1 cm,则PC=______.
11.梯形中位线长10 cm,一条对角线将中位线分成的两部分之差是3 cm,则该梯形中的较大的底是______cm.
12.如图,F是AB的中点,FG∥BC,EG∥CD,则AG= .AE= .
答案:GC ED
13.如图所示,在等腰梯形ABCD中,AB∥CD,AD=12 cm, AC交梯形中位线EG于点F.若EF=4 cm,FG=10 cm求梯形ABCD的面积.
解析:作高DM、CN,则四边形DMNC为矩形.∵EG是梯形ABCD的中位线,∴EG∥DC∥AB.∴F是AC的中点.∴DC=2EF=8 cm,AB=2FG=20 cm,MN=DC=8 cm.在Rt△ADM和Rt△BCN中,AD=BC,∠DAM=∠CBN,∠AMD=∠BNC,∴△ADM≌△BCN.∴AM=BN= (20-8)=6 cm.∴DM= = =6 cm.∴S梯形=EG·DM=14×6 =84 (cm2).
14.如图所示,在梯形ABCD中,AD∥BC,DC⊥BC,E为AB的中点.求证:EC=ED.
证明:过点E作EF∥BC交DC于点F.在梯形ABCD中,AD∥BC,∴AD∥EF∥BC.∵E是AB的中点,∴F是DC的中点.∵∠BCD=90°,∴∠DFE=90°.∴EF⊥DC于点F,且F是DC的中点,∴EF是线段DC的垂直平分线.∴EC=ED.(线段垂直平分线上的点到线段两端点距离相等)
1.平行线等分线段定理的条件是a、b、c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a、b、c相交,即被平行线a、b、c所截.2.平行线的条数还可以更多,可以推广.3.平行线等分线段定理的逆命题是:如果一组直线截另一组直线成相等的线段,那么这组直线平行.可以证明这一命题是错误的(如图所示).
4.三角形中位线定理的内容是:三角形中位线平行于第三边,并且等于它的一半.5.梯形中位线的定义是:连接梯形两腰中点的线段叫做梯形的中位线,这是要强调梯形中位线是连接两腰中点的线段,而不是连接两底中点的线段的一半.6.梯形中位线定理的内容是:梯形中位线平行于两底,并且等于上、下两底和的一半.7.平行线等分线段定理的推论2:“过梯形一腰的中点与底平行的直线必平分另一腰”,或说成“过梯形一腰中点与底边平行的直线为梯形的中位线”,利用它可以判定某一线段为梯形中位线.8.梯形中位线是梯形中的重要线段,它的性质可以为许多问题的证明和求解提供依据,在几何中有着举足轻重的地位.
高中数学人教版新课标A选修4-1二 平行线分线段成比例定理授课ppt课件: 这是一份高中数学人教版新课标A选修4-1二 平行线分线段成比例定理授课ppt课件,共37页。PPT课件主要包含了成比例,∶10,答案1等内容,欢迎下载使用。
人教版新课标A选修4-1一 平行线等分线段定理教学演示ppt课件: 这是一份人教版新课标A选修4-1一 平行线等分线段定理教学演示ppt课件,共28页。PPT课件主要包含了平行线,第三边,另一腰等内容,欢迎下载使用。
人教版新课标A选修4-1五 与圆有关的比例线段课文课件ppt: 这是一份人教版新课标A选修4-1五 与圆有关的比例线段课文课件ppt,共32页。PPT课件主要包含了第3题图,第4题图等内容,欢迎下载使用。













