2021学年3.2立体几何中的向量方法课后作业题

这是一份2021学年3.2立体几何中的向量方法课后作业题，共11页。
[时间：45分钟 分值：100分]

eq \a\vs4\al\c1(基础热身)
1．已知向量m，n分别是直线l和平面α的方向向量和法向量，若cs〈m，n〉＝－eq \f(1,2)，则l与α所成的角为( )
A．30° B．60° C．120° D．150°
2．若平面α，β的法向量分别为a＝(－1,2,4)，b＝(x，－1，－2)，并且α⊥β，则x的值为( )
A．10 B．－10 C.eq \f(1,2) D．－eq \f(1,2)
3．两平行平面α，β分别经过坐标原点O和点A(2,1,1)，且两平面的一个法向量n＝(－1,0,1)，则两平面间的距离是( )
A.eq \f(3,2) B.eq \f(\r(2),2) C.eq \r(3) D．3eq \r(2)
4．已知平面α内有一个点A(2，－1,2)，α的一个法向量为n＝(3,1,2)，则下列点P中，在平面α内的是( )
A．(1，－1,1) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(1，3，\f(3,2)))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(1，－3，\f(3,2))) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(－1，3，\f(3,2)))
eq \a\vs4\al\c1(能力提升)
5．如图K42－1，长方体ABCD－A1B1C1D1中，底面是边长为2的正方形，高为1，则异面直线AD1和C1D所成角的余弦值是( )
图K42－1
A.eq \f(\r(5),5) B．－eq \f(\r(5),5) C.eq \f(1,5) D.eq \f(2,5)
6．在平行四边形ABCD中，AB＝AC＝1，∠ACD＝90°，将它沿对角线AC折起，使AB和CD成60°角(如图K43－2)，则B、D间的距离为( )
图K42－2
A．1 B．2 C.eq \r(2) D．2或eq \r(2)
7．三棱锥的三条侧棱两两互相垂直，长度分别为6,4,4，则其顶点到底面的距离为( )
A.eq \f(14,3) B．2eq \r(17) C.eq \f(6\r(22),11) D.eq \f(2\r(17),3)
8．在棱长为1的正方体ABCD－A1B1C1D1中，E、F分别为棱AA1、BB1的中点，G为棱A1B1上的一点，且A1G＝λ(0≤λ≤1)，则点G到平面D1EF的距离为( )
A.eq \r(3) B.eq \f(\r(2),2) C.eq \f(\r(2)λ,3) D.eq \f(\r(5),5)
图K42－3
9．如图K42－3，四棱锥P－ABCD中，底面ABCD是矩形，PD⊥平面ABCD，且PD＝AD＝1，AB＝2，点E是AB上一点，当二面角P－EC－D的平面角为eq \f(π,4)时，AE＝( )
A．1 B.eq \f(1,2) C．2－eq \r(2) D．2－eq \r(3)
10．已知三棱锥O－ABC的侧棱OA，OB，OC两两垂直，E为OC的中点，且OA＝1，OB＝OC＝2，则平面EAB与平面ABC夹角的余弦值是________．
11．如图K42－4，已知四棱柱ABCD－A1B1C1D1中，底面ABCD是边长为a的正方形，侧棱AA1长为b，且AA1与A1B1，A1D1的夹角都是60°，则AC1的长等于________．
图K42－4
图K42－5
12．如图K42－5，AO⊥平面α，BC⊥OB，BC与平面α的夹角为30°，AO＝BO＝BC＝a，则AC＝________.
13．如图K42－6，正方体ABCD－A1B1C1D1的棱长为2，M，N分别是C1D1，CC1的中点，则直线B1N与平面BDM所成角的正弦值为________．
图K42－6
14．(10分)如图K42－7，放置在水平面上的组合体由直三棱柱ABC－A1B1C1与正三棱锥B－ACD组成，其中，AB⊥BC.它的正视图、俯视图、侧视图的面积分别为2eq \r(2)＋1,2eq \r(2)＋1,1.
(1)求直线CA1与平面ACD所成角的正弦值；
(2)在线段AC1上是否存在点P，使B1P⊥平面ACD？若存在，确定点P的位置；若不存在，说明理由．
图K42－7
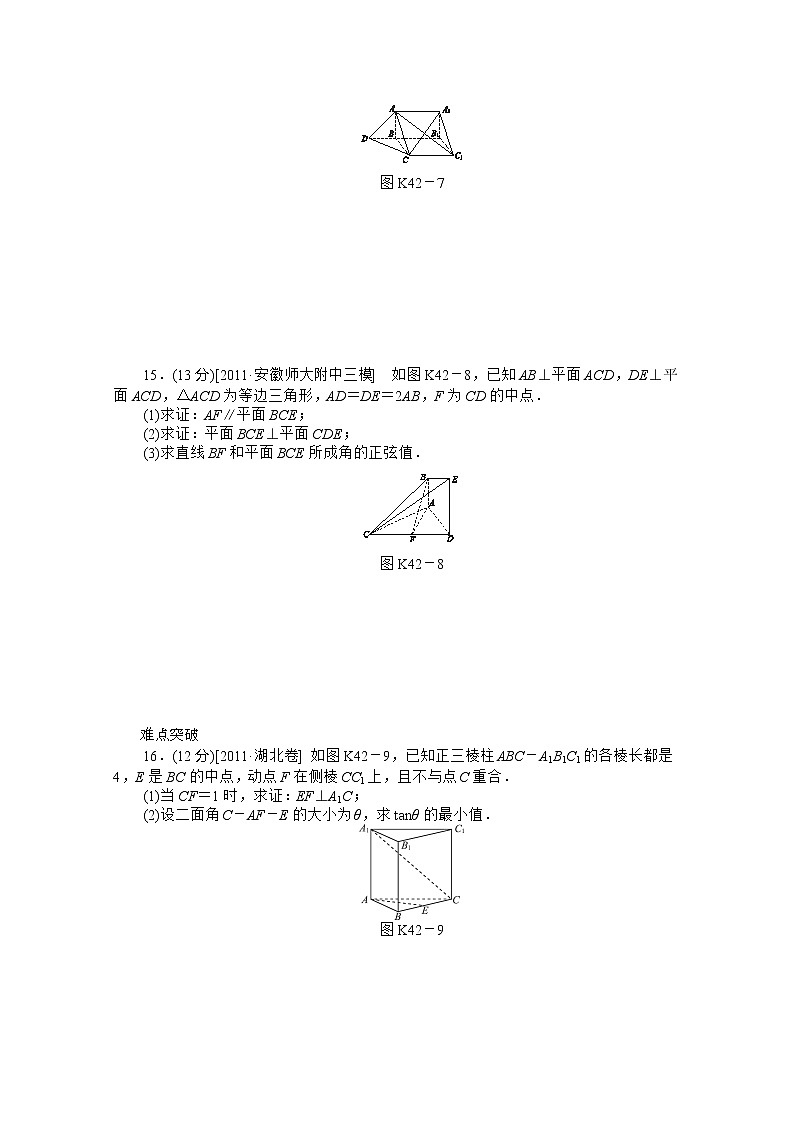
15．(13分)[2011·安徽师大附中三模] 如图K42－8，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB，F为CD的中点．
(1)求证：AF∥平面BCE；
(2)求证：平面BCE⊥平面CDE；
(3)求直线BF和平面BCE所成角的正弦值．
图K42－8
eq \a\vs4\al\c1(难点突破)
16．(12分)[2011·湖北卷] 如图K42－9，已知正三棱柱ABC－A1B1C1的各棱长都是4，E是BC的中点，动点F在侧棱CC1上，且不与点C重合．
(1)当CF＝1时，求证：EF⊥A1C；
(2)设二面角C－AF－E的大小为θ，求tanθ的最小值．
图K42－9
课时作业(四十二)
【基础热身】
1．A [解析] 由于cs〈m，n〉＝－eq \f(1,2)，∴〈m，n〉＝120°，所以直线l与α所成的角为30°.
2．B [解析] ∵α⊥β，∴a·b＝0，∴x＝－10.
3．B [解析] 两平面的一个单位法向量n0＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(2),2)，0，\f(\r(2),2)))，故两平面间的距离d＝|eq \(OA,\s\up6(→))·n0|＝eq \f(\r(2),2).
4．B [解析] 对于选项A，eq \(PA,\s\up6(→))＝(1,0,1)，则eq \(PA,\s\up6(→))·n＝(1,0,1)·(3,1,2)＝5≠0，故排除A；对于选项B，eq \(PA,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(1，－4，\f(1,2)))，则eq \(PA,\s\up6(→))·n＝eq \b\lc\(\rc\)(\a\vs4\al\c1(1，－4，\f(1,2)))·(3,1,2)＝0，验证可知C、D均不满足eq \(PA,\s\up6(→))·n＝0.
【能力提升】
5．C [解析] 建立如图所示的空间直角坐标系．则A(2,0,0)，D(0,0,0)，D1(0,0,1)，C1(0,2,1)，eq \(AD,\s\up6(→))1＝(－2,0,1)，eq \(DC1,\s\up6(→))＝(0,2,1)，故异面直线AD1和C1D所成角的余弦值为|cs〈eq \(AD,\s\up6(→))1，eq \(DC,\s\up6(→))1〉|＝eq \f(|\(AD,\s\up6(→))1·\(DC,\s\up6(→))1|,|\(AD,\s\up6(→))1||\(DC,\s\up6(→))1|)＝eq \f(1,5).
6．D [解析] ∵∠ACD＝90°，∴eq \(AC,\s\up6(→))·eq \(CD,\s\up6(→))＝0.
同理eq \(BA,\s\up6(→))·eq \(AC,\s\up6(→))＝0，
∵AB和CD成60°角，∴〈eq \(BA,\s\up6(→))，eq \(CD,\s\up6(→))〉＝60°或120°.
∵eq \(BD,\s\up6(→))＝eq \(BA,\s\up6(→))＋eq \(AC,\s\up6(→))＋eq \(CD,\s\up6(→))，
∴eq \(BD,\s\up6(→))2＝eq \(BA,\s\up6(→))2＋eq \(AC,\s\up6(→))2＋eq \(CD,\s\up6(→))2＋2eq \(BA,\s\up6(→))·eq \(CD,\s\up6(→))＋2eq \(BA,\s\up6(→))·eq \(AC,\s\up6(→))＋2eq \(AC,\s\up6(→))·eq \(CD,\s\up6(→))
＝eq \(BA,\s\up6(→))2＋eq \(AC,\s\up6(→))2＋eq \(CD,\s\up6(→))2＋2eq \(BA,\s\up6(→))·eq \(CD,\s\up6(→))
＝3＋2×1×1×cs〈eq \(BA,\s\up6(→))，eq \(CD,\s\up6(→))〉
＝eq \b\lc\{\rc\ (\a\vs4\al\c1(4〈\(BA,\s\up6(→))，\(CD,\s\up6(→))〉＝60°，,2〈\(BA,\s\up6(→))，\(CD,\s\up6(→))〉＝120°，))
∴|eq \(BD,\s\up6(→))|＝2或eq \r(2)，即B、D间的距离为2或eq \r(2)，故选D.
7．C [解析] 设三棱锥为P－ABC，且PA＝6，PB＝PC＝4，以P为原点建立空间直角坐标系如图，则P(0,0,0)，A(6,0,0)，B(0,4,0)，C(0,0,4)，eq \(PA,\s\up6(→))＝(6,0,0)，eq \(AB,\s\up6(→))＝(－6,4,0)，eq \(AC,\s\up6(→))＝(－6,0,4)，设面ABC的一个法向量为n＝(x，y，z)，则n⊥eq \(AB,\s\up6(→))，n⊥eq \(AC,\s\up6(→))，
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(－6x＋4y＝0，,－6x＋4z＝0))⇒y＝z＝eq \f(3,2)x，所以可选面ABC的一个法向量为n＝(2,3,3)，
所以P到面ABC的距离d＝|eq \(PA,\s\up6(→))||cs〈eq \(PA,\s\up6(→))，n〉|＝eq \f(|\(PA,\s\up6(→))·n|,|n|)＝eq \f(12,\r(4＋9＋9))＝eq \f(6\r(22),11)，选C.
8．D [解析] 如图，如果过点G直接向平面D1EF作垂线，垂足为H，如果我们能求出向量eq \(GH,\s\up6(→))，那么|eq \(GH,\s\up6(→))|就是点G到平面D1EF的距离．在正方体中，建立空间直角坐标系非常方便，因此用坐标的方法，解决这个问题．
如图，以射线DA，DC，DD1分别为x，y，z轴的正方向建立空间直角坐标系，则G(1，λ，1)，Eeq \b\lc\(\rc\)(\a\vs4\al\c1(1，0，\f(1,2)))，eq \(GE,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(0，－λ，－\f(1,2)))，Feq \b\lc\(\rc\)(\a\vs4\al\c1(1，1，\f(1,2)))，eq \(EF,\s\up6(→))＝(0,1,0)，D1(0,0,1)，eq \(ED,\s\up6(→))1＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－1，0，\f(1,2))).过点G向平面D1EF作垂线，垂足为H，由于点H在平面D1EF内，故存在实数x，y使eq \(GH,\s\up6(→))＝eq \(GE,\s\up6(→))＋xeq \(EF,\s\up6(→))＋yeq \(ED,\s\up6(→))1＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－y，－λ＋x，－\f(1,2)＋\f(1,2)y))，由于GH⊥EF，GH⊥ED1，
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(－y，－λ＋x，－\f(1,2)＋\f(1,2)y))·0，1，0＝0，,\b\lc\(\rc\)(\a\vs4\al\c1(－y，－λ＋x，－\f(1,2)＋\f(1,2)y))·\b\lc\(\rc\)(\a\vs4\al\c1(－1，0，\f(1,2)))＝0，))
解得eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝λ，,y＝\f(1,5)，))故eq \(GH,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,5)，0，－\f(2,5)))，所以|eq \(GH,\s\up6(→))|＝eq \f(\r(5),5)，即点G到平面D1EF的距离是eq \f(\r(5),5).
9．D [解析] 以D为原点，射线DA，DC，DP为x，y，z轴正方向建立空间直角坐标系，如图，
设E(1，y0,0)(0≤y0≤2)，则eq \(EC,\s\up6(→))＝(－1,2－y0,0)，
设平面PEC的法向量为n1＝(x，y，z)，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(n1·\(EC,\s\up6(→))＝0，,n1·\(PC,\s\up6(→))＝0))⇒eq \b\lc\{\rc\ (\a\vs4\al\c1(－x＋y2－y0＝0，,2y－z＝0))⇒x∶y∶z＝(2－y0)∶1∶2，
记n1＝(2－y0,1,2)，
而平面ECD的法向量n2＝(0,0,1)，则二面角P－EC－D的平面角θ满足csθ＝|cs〈n1，n2〉|＝eq \f(\r(2),2)，
∴csθ＝eq \f(|n1·n2|,|n1|·|n2|)＝eq \f(2,\r(2－y02＋12＋22)·1)＝eq \f(\r(2),2)⇒y0＝2－eq \r(3).
∴当AE＝2－eq \r(3)时，二面角P－EC－D的平面角为eq \f(π,4).
10.eq \f(7\r(6),18) [解析] 以O为原点，OB，OC，OA分别为x，y，z轴建立空间直角坐标系，则有A(0,0,1)，B(2,0,0)，C(0,2,0)，E(0,1,0)．
设平面ABC的法向量为n1＝(x，y，z)，则由n1⊥eq \(AB,\s\up6(→))知n1·eq \(AB,\s\up6(→))＝2x－z＝0，由n1⊥eq \(AC,\s\up6(→))知n1·eq \(AC,\s\up6(→))＝2y－z＝0，取n1＝(1,1,2)．
设平面EAB的法向量为n＝(x，y，z)，则由n⊥eq \(AB,\s\up6(→))知n·eq \(AB,\s\up6(→))＝2x－z＝0，由n⊥eq \(EB,\s\up6(→))知n·eq \(EB,\s\up6(→))＝2x－y＝0，取n＝(1,2,2)．
则cs〈n，n1〉＝eq \f(n·n1,|n||n1|)＝eq \f(1＋2＋4,\r(9)×\r(6))＝eq \f(7\r(6),18)，
所以平面EAB与平面ABC夹角的余弦值为eq \f(7\r(6),18).
11.eq \r(2a2＋b2－2ab) [解析] 由已知〈eq \(AA,\s\up6(→))1，eq \(AB,\s\up6(→))〉＝〈eq \(AA,\s\up6(→))1，eq \(AD,\s\up6(→))〉＝120°，〈eq \(AB,\s\up6(→))，eq \(AD,\s\up6(→))〉＝90°.
|eq \(AC,\s\up6(→))1|2＝|eq \(AA,\s\up6(→))1＋eq \(AB,\s\up6(→))＋eq \(AD,\s\up6(→))|2＝|eq \(AA,\s\up6(→))1|2＋|eq \(AB,\s\up6(→))|2＋|eq \(AD,\s\up6(→))|2＋2eq \(AA,\s\up6(→))1·eq \(AB,\s\up6(→))＋2eq \(AB,\s\up6(→))·eq \(AD,\s\up6(→))＋2eq \(AA,\s\up6(→))1·eq \(AD,\s\up6(→))
＝b2＋a2＋a2－ab－ab＝2a2＋b2－2ab，
故|eq \(AC,\s\up6(→))1|＝eq \r(2a2＋b2－2ab).
12.eq \r(2)a [解析] eq \a\vs4\al(\(AC,\s\up6(→)))＝eq \(AO,\s\up6(→))＋eq \(OB,\s\up6(→))＋eq \(BC,\s\up6(→))，
其中〈eq \(AO,\s\up6(→))，eq \(OB,\s\up6(→))〉＝〈eq \(OB,\s\up6(→))，eq \(BC,\s\up6(→))〉＝90°，〈eq \(AO,\s\up6(→))，eq \(BC,\s\up6(→))〉＝120°，
故|eq \(AC,\s\up6(→))|2＝|eq \(AO,\s\up6(→))＋eq \(OB,\s\up6(→))＋eq \(BC,\s\up6(→))|2＝|eq \(AO,\s\up6(→))|2＋|eq \(OB,\s\up6(→))|2＋|eq \(BC,\s\up6(→))|2＋2eq \(AO,\s\up6(→))·eq \(OB,\s\up6(→))＋2eq \(OB,\s\up6(→))·eq \(BC,\s\up6(→))＋2eq \(AO,\s\up6(→))·eq \(BC,\s\up6(→))
＝3a2＋2a2cs120°＝2a2，故|eq \(AC,\s\up6(→))|＝eq \r(2)a，即AC＝eq \r(2)a.
13.eq \f(\r(5),3) [解析] 以D为坐标原点，分别以eq \(DA,\s\up6(→))，eq \(DC,\s\up6(→))，eq \(DD1,\s\up6(→))的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，如图，则B1(2,2,2)，N(0,2,1)，M(0,1,2)，D(0,0,0)，B(2,2,0), eq \(NB1,\s\up6(→))＝(2,0,1)，
eq \(DB,\s\up6(→))＝(2,2,0)，eq \(DM,\s\up6(→))＝(0,1,2)，可得平面BDM的一个法向量n＝(2，－2,1)．因为cs〈n，eq \(NB1,\s\up6(→))〉＝eq \f(n·\(NB1,\s\up6(→)),|n|·|\(NB,\s\up6(→))|)＝eq \f(\r(5),3)，故直线B1N与平面BDM所成角的正弦值是eq \f(\r(5),3).
14．[解答] 由已知可得AB⊥平面BB1C1C，由于三棱锥B－ACD是正三棱锥，所以CD⊂平面BB1C1C，D，B，B1三点共线，AB＝BC＝BD.
设AB＝a，BB1＝b.则其正视图和俯视图的面积都是ab＋eq \f(1,2)a2，侧视图的面积是eq \f(1,2)a2，根据已知解得a＝eq \r(2)，b＝2.以点B为坐标原点，射线BC，BB1，BA分别为x，y，z轴的正方向建立空间直角坐标系，如图，则
A(0,0，eq \r(2))，C(eq \r(2)，0,0)，D(0，－eq \r(2)，0)，B1(0,2,0)，C1(eq \r(2)，2,0)，A1(0,2，eq \r(2))．
(1)由于三棱锥B－ACD是正三棱锥，该三棱锥的重心Geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),3)，－\f(\r(2),3)，\f(\r(2),3)))，则BG⊥平面ACD，故可取向量n＝(1，－1,1)为平面ACD的一个法向量，eq \(CA1,\s\up6(→))＝(－eq \r(2)，2，eq \r(2))，故可取v＝(1，－eq \r(2)，－1)为直线CA1的一个方向向量．设直线CA1与平面ACD所成角为θ，则
sinθ＝|cs〈n，v〉|＝eq \f(|n·v|,|n||v|)＝eq \f(\r(2),2\r(3))＝eq \f(\r(6),6).
(2)设eq \(AP,\s\up6(→))＝meq \(AC1,\s\up6(→))＝(eq \r(2)m,2m，－eq \r(2)m)，则eq \(B1P,\s\up6(→))＝eq \(B1A,\s\up6(→))＋eq \(AP,\s\up6(→))＝(eq \r(2)m,2m－2，eq \r(2)－eq \r(2)m)，
如果B1P⊥平面ACD，则eq \(B1P,\s\up6(→))∥n，即(eq \r(2)m,2m－2，eq \r(2)－eq \r(2)m)＝(λ，－λ，λ)，由此得方程组
eq \b\lc\{\rc\ (\a\vs4\al\c1(\r(2)m＝λ，①,2m－2＝－λ，②,\r(2)－\r(2)m＝λ，③))
由①③得m＝eq \f(1,2)，λ＝eq \f(\r(2),2)，代入②则－1＝－eq \f(\r(2),2)，矛盾，这说明不存在满足题目要求的点P.
15．[解答] 方法一：
(1)证法一：取CE的中点G，连接FG、BG.
∵F为CD的中点，∴GF∥DE且GF＝eq \f(1,2)DE，
∵AB⊥平面ACD，DE⊥平面ACD，
∴AB∥DE，∴GF∥AB.
又AB＝eq \f(1,2)DE，∴GF＝AB.又DE＝2AB，
∴四边形GFAB为平行四边形，则AF∥BG.
∵AF⊄平面BCE，BG⊂平面BCE，
∴AF∥平面BCE.
证法二：取DE的中点M，连接AM、FM，
∵F为CD的中点，∴FM∥CE.
∵AB⊥平面ACD，DE⊥平面ACD，∴DE∥AB.
又AB＝eq \f(1,2)DE＝ME，
∴四边形ABEM为平行四边形，则AM∥BE.
∵FM、AM⊄平面BCE，CE、BE⊂平面BCE，
∴FM∥平面BCE，AM∥平面BCE.
又FM∩AM＝M，∴平面AFM∥平面BCE.
∵AF⊂平面AFM，
∴AF∥平面BCE.
(2)证明：∵△ACD为等边三角形，F为CD的中点，
∴AF⊥CD.
∵DE⊥平面ACD，AF⊂平面ACD，∴DE⊥AF.
又CD∩DE＝D，故AF⊥平面CDE.
∵BG∥AF，∴BG⊥平面CDE.
∵BG⊂平面BCE，
∴平面BCE⊥平面CDE.
(3)在平面CDE内，过F作FH⊥CE于H，连接BH，
∵平面BCE⊥平面CDE，∴FH⊥平面BCE.
∴∠FBH为BF和平面BCE所成的角．
设AD＝DE＝2AB＝2a，则FH＝CFsin45°＝eq \f(\r(2),2)a，
BF＝eq \r(AB2＋AF2)＝eq \r(a2＋\r(3)a2)＝2a，
在Rt△FHB中，sin∠FBH＝eq \f(FH,BF)＝eq \f(\r(2),4).
∴直线BF和平面BCE所成角的正弦值为eq \f(\r(2),4).
方法二：
设AD＝DE＝2AB＝2a，建立如图所示的坐标系A－xyz，则A(0,0,0)，C(2a,0,0)，B(0,0，a)，D(a，eq \r(3)a,0)，E(a，eq \r(3)a,2a)．
∵F为CD的中点，∴Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)a，\f(\r(3),2)a，0)).
(1)证明：eq \(AF,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)a，\f(\r(3),2)a，0))，eq \(BE,\s\up6(→))＝(a，eq \r(3)a，a)，eq \(BC,\s\up6(→))＝(2a,0，－a)，
∵eq \(AF,\s\up6(→))＝eq \f(1,2)(eq \(BE,\s\up6(→))＋eq \(BC,\s\up6(→)))，AF⊄平面BCE，∴AF∥平面BCE.
(2)证明：∵eq \(AF,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)a，\f(\r(3),2)a，0))，eq \(CD,\s\up6(→))＝(－a，eq \r(3)a,0)，eq \(ED,\s\up6(→))＝(0,0，－2a)，
∴eq \(AF,\s\up6(→))·eq \(CD,\s\up6(→))＝0，eq \(AF,\s\up6(→))·eq \(ED,\s\up6(→))＝0，∴eq \(AF,\s\up6(→))⊥eq \(CD,\s\up6(→))，eq \(AF,\s\up6(→))⊥eq \(ED,\s\up6(→)).
∴eq \(AF,\s\up6(→))⊥平面CDE，又AF∥平面BCE，
∴平面BCE⊥平面CDE.
(3)设平面BCE的法向量为n＝(x，y，z)，由n·eq \(BE,\s\up6(→))＝0，n·eq \(BC,\s\up6(→))＝0可得
x＋eq \r(3)y＋z＝0,2x－z＝0，取n＝(1，－eq \r(3)，2)．
又eq \(BF,\s\up6(→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)a，\f(\r(3),2)a，－a))，设BF和平面BCE所成的角为θ，则
sinθ＝eq \f(|\(BF,\s\up6(→))·n|,|\(BF,\s\up6(→))|·|n|)＝eq \f(2a,2a·2\r(2))＝eq \f(\r(2),4).
∴直线BF和平面BCE所成角的正弦值为eq \f(\r(2),4).
【难点突破】
16．[解答] 解法1：过E作EN⊥AC于N，连接EF.
(1)如图①，连接NF、AC1，由直棱柱的性质知，底面ABC⊥侧面A1C，
又底面ABC∩侧面A1C＝AC，且EN⊂底面ABC，所以EN⊥侧面A1C，NF为EF在侧面A1C内的射影，
在Rt△CNE中，CN＝CEcs60°＝1，
则由eq \f(CF,CC1)＝eq \f(CN,CA)＝eq \f(1,4)，得NF∥AC1.
又AC1⊥A1C，故NF⊥A1C，
由三垂线定理知EF⊥A1C.
(2)如图②，连接AF，过N作NM⊥AF于M，连接ME，
由(1)知EN⊥侧面A1C，根据三垂线定理得EM⊥AF，
所以∠EMN是二面角C－AF－E的平面角，即∠EMN＝θ，
设∠FAC＝α，则0°