数学选修2-13.2立体几何中的向量方法评课课件ppt

这是一份数学选修2-13.2立体几何中的向量方法评课课件ppt，共59页。PPT课件主要包含了空间的角，线线角，线面角，设正方体棱长为1，面面角，①方向向量法，二面角的范围，②法向量法，习题课等内容，欢迎下载使用。

空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法，解题时，可用定量的计算代替定性的分析，从而避免了一些繁琐的推理论证。求空间角与距离是立体几何的一类重要的问题，也是高考的热点之一。我们主要研究怎么样用向量的办法解决空间角的问题。
线线角、线面角、面面角。
总之，空间的角最终都可以转化为两相交直线所成的角。因此我们可以考虑通过两个向量的夹角去求这些空间角。
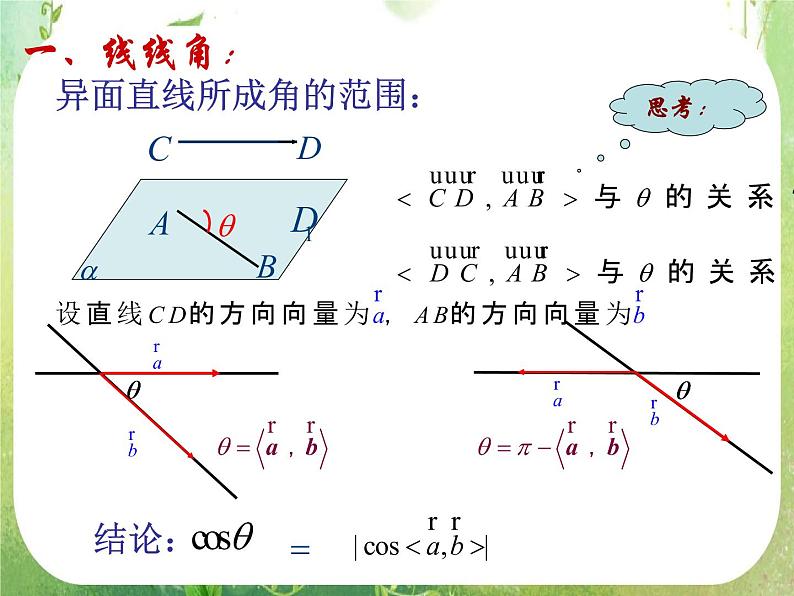
异面直线所成角的范围：
所以 与 所成角的余弦值为
直线与平面所成角的范围：
例三：如图3，甲站在水库底面上的点A处，乙站在水坝斜面上的点B处。从A，B到直线 （库底与水坝的交线）的距离AC和BD分别为 和 ,CD的长为 , AB的长为 。求库底与水坝所成二面角的余弦值。
设向量 与 的夹角为 ， 就是库底与水坝所成的二面角。
所以库底与水坝所成二面角的余弦值为
注意法向量的方向：一进一出，二面角等于法向量夹角；同进同出，二面角等于法向量夹角的补角
1.异面直线所成角：
2.直线与平面所成角：
一进一出，二面角等于法向量的夹角；同进同出，二面角等于法向量夹角的补角。
2、如果平面的一条斜线与它在这个平面上的射影的方向向量分别是 n1=（1，0，1）， n2 =（0，1，1），那么这条斜线与平面所成的角是______ .
3. 三棱锥P-ABC PA⊥ABC,PA=AB=AC, E为PC中点 , ,则PA与BE所成角的余弦值为_________ .
4. 直三棱柱ABC-A1B1C1中, A1A=2, AB=AC=1, 则AC1与截面BB1CC1所成角的余弦值为_________ .
2、如果平面的一条斜线与它在这个平面上的射影的方向向量分别是 =（1，0，1）， =（0，1，1），那么这条斜线与平面所成的角是______ .
3、已知两平面的法向量分别m=(0,1,0),n=(0,1,1)，则两平面所成的钝二面角为______ .
4. 三棱锥P-ABC PA⊥ABC,PA=AB=AC, ,E为PC中点 ,则PA与BE所成角的余弦值为_________ .
5. 直三棱柱ABC-A1B1C1中, A1A=2, AB=AC=1, 则AC1与截面BB1CC1所成角的余弦值为_________ .
6.正方体中ABCD-A1B1C1D1中E为A1D1的中点, 则二面角E-BC-A的大小是________
解法二：同法一，以C为原点建立空间直角坐标系 C-xyz
例1 如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC,E是PC的中点，作EF⊥PB交PB于点F.(1)求证：PA//平面EDB(2)求证：PB⊥平面EFD(3)求二面角C-PB-D的大小。
例2、如图，在四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC 底面ABCD。已知 AB=2，BC=2 ，SA=SB= .(1)求证 (2)求直线SD与平面SAB所成角的正弦值。
例3 如图,在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，PA=AB=1,AD= ，在线段BC上是否存在一点E,使PA与平面PDE所成角的大小为450? 若存在，确定点E的位置；若不存在说明理由。
例4（2006年福建卷）如图，四面体ABCD中，O、E分别是BD、BC的中点，（I）求证：AO⊥平面BCD；（II）求异面直线AB与CD所成角的大小；（III）求点E到平面ACD的距离。
解：如图所示建立空间直角坐标系，点D为坐标原点，设DC=1
(1)证明：连结AC,AC交BD于点G,连结EG
(2)求证：PB⊥平面EFD
(3)求二面角C-PB-D的大小。
例2、如图，在四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC 底面ABCD。已知 AB=2，BC= 2 ，SA=SB= .(1)求证 (2)求直线SD与平面SAB所成角的正弦值。
证明：(1)取BC中点O，连接OA、OS。
(2)求直线SD与平面SAB所成角的正弦值。
所以直线SD与平面SAB所成角的正弦值为
解：以A为原点，AD、AB、AP所在的直线分别为x轴、y轴、z轴，建立空间直角坐标系，
解：（I）略 （II）解：以O为原点，如图建立空间直角坐标系，
所以异面直线AB与CD所成角的余弦值为
（III）解：设平面ACD的法向量为
是平面ACD的一个法向量，又
所以点E到平面ACD的距离
例5、(2004，天津)如图所示，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD 底面ABCD，PD=DC，E是PC的中点。(1)证明：PA//平面EDB；(2)求EB与底面ABCD所成的角的正切值。
(1)证明：设正方形边长为1，则PD=DC=DA=1.连AC、BD交于G点
(2)求EB与底面ABCD所成的角的正切值。
1、如图，已知：直角梯形OABC中， OA∥BC,∠AOC=90°，SO⊥面OABC， 且OS=OC=BC=1，OA=2。求：(1)异面直线SA和OB所成的角的余弦值 (2)OS与面SAB所成角的余弦值 (3)二面角B－AS－O的余弦值
1、如图，已知：直角梯形OABC中， OA∥BC,∠AOC=90°，SO⊥面OABC， 且OS=OC=BC=1，OA=2。求：(1)异面直线SA和OB所成的 角的余弦值
1、如图，已知：直角梯形OABC中， OA∥BC,∠AOC=90°，SO⊥面OABC， 且OS=OC=BC=1，OA=2。求：(2)OS与面SAB所成角的余弦值
所以OS与面SAB所成角的余弦值为
1、如图，已知：直角梯形OABC中， OA∥BC,∠AOC=90°，SO⊥面OABC， 且OS=OC=BC=1，OA=2。求：(3)二面角B－AS－O的余弦值
2、在如图的实验装置中，正方形框架的边长都是1，且平面ABCD与平面ABEF互相垂直。活动弹子M，N分别在正方形对角线AC和BF上移动，且CM和BN的长度保持相等，记CM=BN= （1）求MN的长；（2）a 为何值时？MN的长最小？（3）当MN的长最小时，求面MNA与面MNB所成二面角的余弦值。