高中数学人教版新课标A选修1-21.1回归分析的基本思想及其初步应用评课ppt课件
展开2、线性回归模型y=bx+a+e
3、线性相关关系强弱的判断:相关系数r
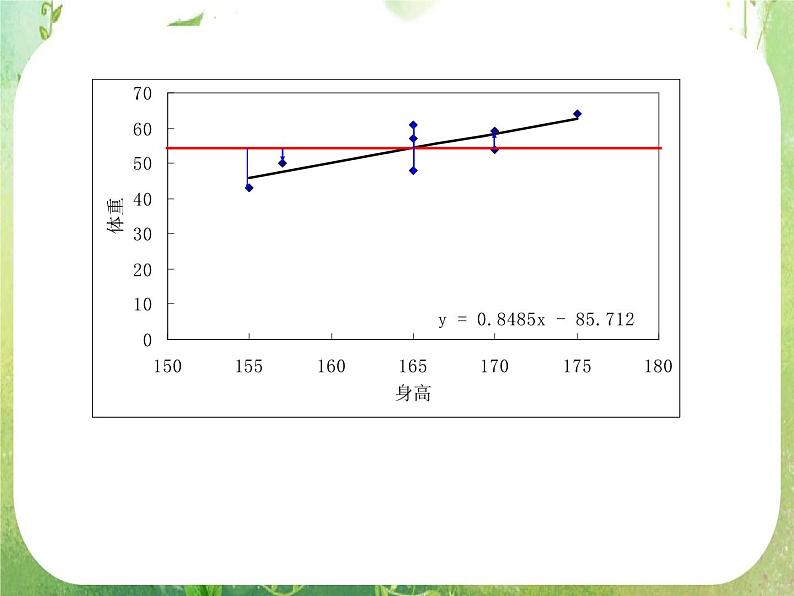
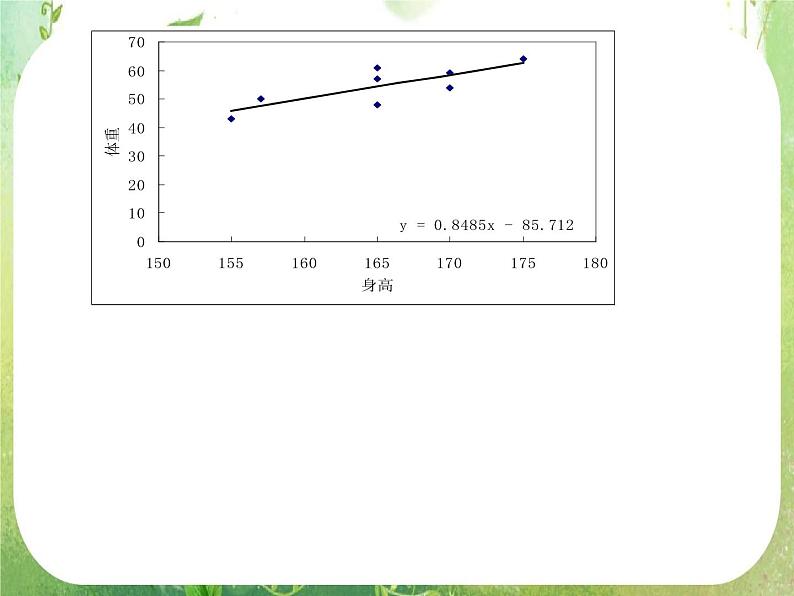
例1:从某大学中随机选取8名女大学生,其身高和体重数据如下表,求根据女大学生的身高预报体重的回归方程,并预报一名身高为172cm的女大学生的体重.
线性回归模型: y=0.849x-85.712+e
身高、随机误差对体重有没有影响?
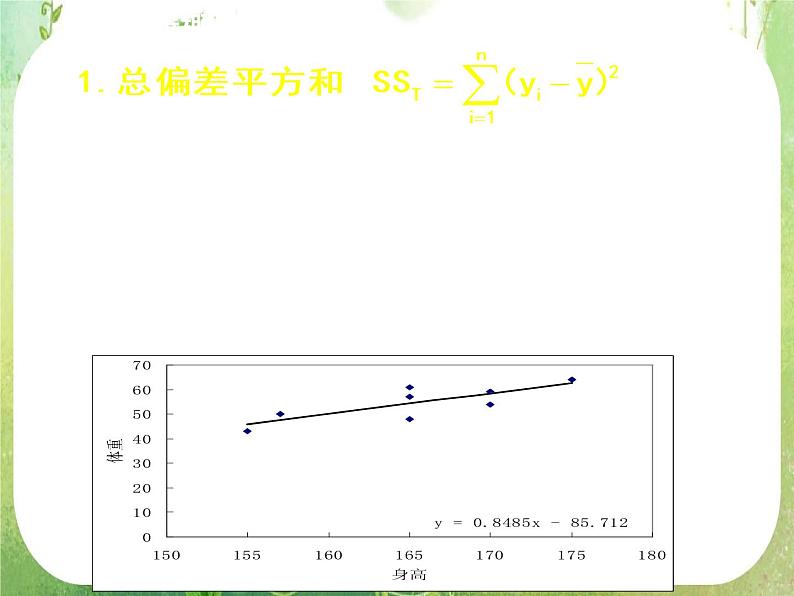
计算例1中总偏差平方和 SST=354
思考:预报变量(体重)与实际值有偏差即总偏差平方和,这个偏差变化在多大程度上与解释变量(身高)有关?在多大程度上与随机变量有关?
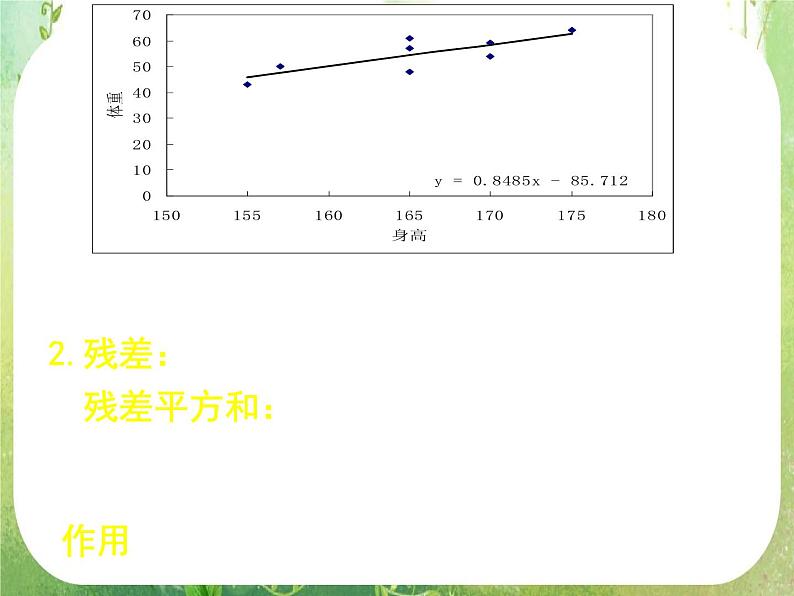
作用:表示随机误差的效应
残差平方和:样本值与回归值差的平方和
例1 SSE=128.361
思考:若体重仅受身高的影响,散点图又如何?
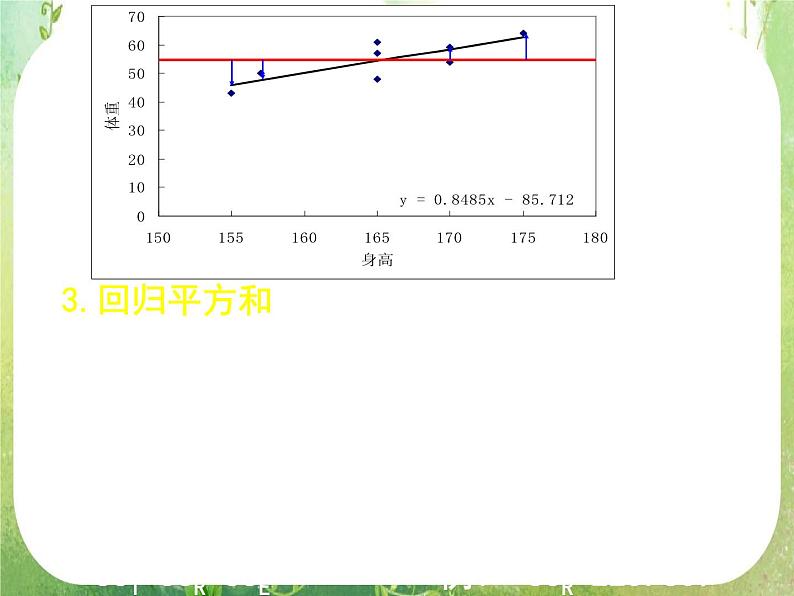
3.回归平方和:相应回归值与样本均值差的平方和,即:
SST=SSR+SSE
作用:表示解释变量的效应
例1 SSR=225.639
即刻画了预报变量的变化中由解释变量通过线性回归模型所引起的那部分变化程度
注:当总偏差平方和相对固定时,残差平方和越小,则回归平方和越大,此时模型的拟合效果越好 .
4.有没有其他方法来刻划模型的拟合程度?
1)R2越大,说明残差平方和越小,回归平方和越大,则模型拟合效果越好。
2)R2表示解释变量对预报变量变化的贡献率
3)R2→1,模型拟合效果越好,表示解释变量和预报变量的相关性越强。
例1 相关指数R2=0.64,说明了什么?
解释变量对总效应约贡献了64%,随机误差贡献了剩余的36%。
4)若采用了几种不同回归方程进行回归分析,通过比较R2值作出选择,即选择R2大的模型作为这组数据的模型。
问:有些时候,样本数据中难免混有错误数据,通过何种方法把它剔除?
判断原始数据中是否存在可疑数据,这方面的工作称为残差分析。
1)计算每组数据的残差
2)画残差图。纵坐标为残差,横坐标为自变量。
残差比较均匀地落在带状区域内,说明选用的模型比较合适。
但第1个点与第6个点残差较大,需要分析。
例1用身高预测体重要注意的问题:
(1)回归方程所适用样本的总体
(2)回归方程所适用的时间性
(3)回归方程所适用的范围
(4)回归方程得到的是预报变量可能取值的平均值
(1)明确研究对象,设好变量
(3)选定回归方程类型
(4)求回归方程中的参数
(5)作残差图,进行残差分析
例2 关于x与y有如下数据:
为了对x、y两个变量进行统计分析,现有以下两种线性模型:y=6.5x+17.5,y=7x+17,试比较哪一个模型拟合的效果更好.
高中数学人教版新课标A选修2-33.1回归分析的基本思想及其初步应用教课课件ppt: 这是一份高中数学人教版新课标A选修2-33.1回归分析的基本思想及其初步应用教课课件ppt,
高中数学人教版新课标A选修2-33.1回归分析的基本思想及其初步应用多媒体教学课件ppt: 这是一份高中数学人教版新课标A选修2-33.1回归分析的基本思想及其初步应用多媒体教学课件ppt,
数学选修2-33.1回归分析的基本思想及其初步应用课堂教学课件ppt: 这是一份数学选修2-33.1回归分析的基本思想及其初步应用课堂教学课件ppt,