初中数学人教版八年级下册第二十章 数据的分析综合与测试复习ppt课件

这是一份初中数学人教版八年级下册第二十章 数据的分析综合与测试复习ppt课件，

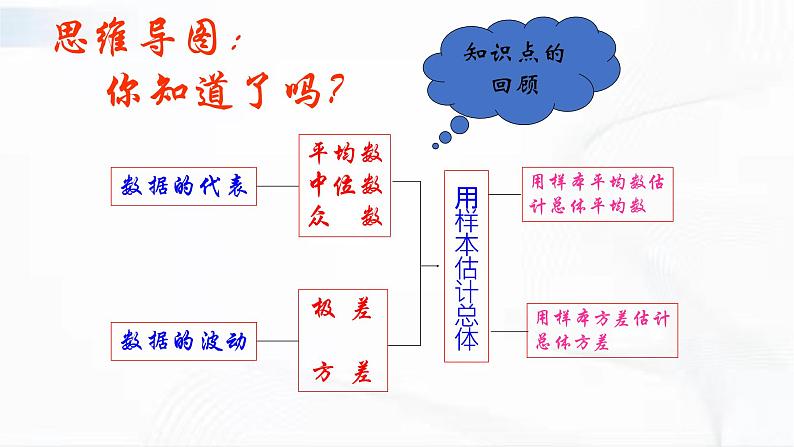
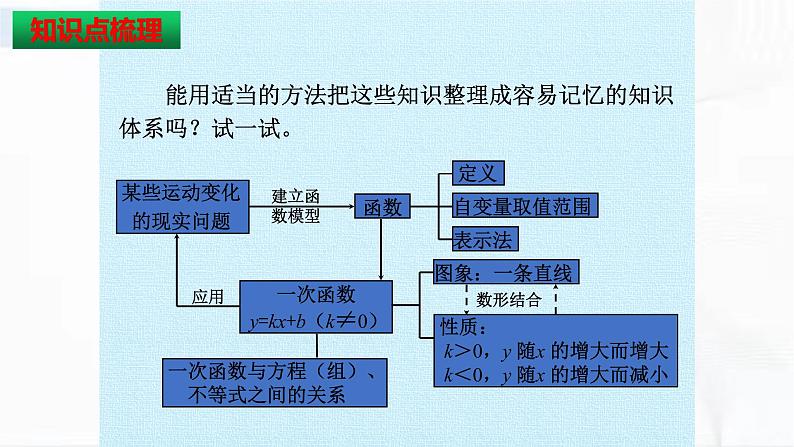
章节复习思维导图： 你知道了吗？知识点的回顾数据的代表数据的波动平均数中位数众 数极 差方 差用样本估计总体用样本平均数估计总体平均数用样本方差估计总体方差1、用样本估计总体是统计的基本思想。在生活和生产中，为了解总体的情况，我们经常采用从总体中抽取样本，通过对样本的调查，获得关于样本的数据和结论，再利用样本的结论对总体进行估计。2、举例说明平均数、中位数、众数的意义。3、了解算术平均数与加权平均数有什么联系和区别。举例说明加权平均数中“权”的意义。4、举例说明极差和方差是怎样刻画数据的波动情况的。知识点梳理问题1：求加权平均数的公式是什么？在求n个数的算术平均数时，如果x1出现f1次，x2出现f2次，…，xk出现fk次（这里f1+f2+…+fk=n）那么这n个数的算术平均数叫做这n个数的加权平均数。知识点梳理　　将一组数据按照由小到大（或由大到小）的顺序排列如果数据的个数是奇数，则处于中间位置的数就是这组数据的 。如果数据的个数是偶数，则中间两个数据的平均数就是这组数据的 。　　中位数是一个位置代表值。如果已知一组数据的中位数，那么可以知道，小于等于或大于等于这个中位数的数据各占一半。　　一组数据中出现次数最多的数据就是这组数据的 。中位数中位数众数知识点梳理平均数、中位数、众数比较1、联系：平均数、中位数和众数都可以作为一组数据的代表，是描述一组数据集中趋势的量，平均数是应用较多的一种量。实际问题中求得的平均数、众数、中位数应带上相应的单位。2、区别：①平均数计算要用到所有数据，它能充分利用所有的数据信息，任何一个数据的变动都会相应引起平均数的变动，并且它受极端值的影响较大；②中位数仅与数据的排列位置有关，某些数据的移动对中位数没有影响，中位数可能出现在所给数据中也可能不在所给的数据中，当一组数据中的个别数据变动较大时，可用中位数描述其趋势；③众数是当一组数据中某一数据重复出现较多时，人们往往关心的一个量，众数不受极端值的影响，它是它的一个优势。知识点梳理★极差：一组数据中最大数据与最小数据的差。极差是最简单的一种度量数据波动情况的量,但只能反映数据的波动范围,不能衡量每个数据的变化情况,而且受极端值的影响较大. ※各数据与平均数的差的平方的平均数叫做这组数据的方差。公式为：方差越小，波动越小。方差越大，波动越大。知识点梳理　　能用适当的方法把这些知识整理成容易记忆的知识体系吗？试一试。知识点梳理2.某校五个绿化小组一天植树的棵数如下：10，10，12，x，8。已知这组数据的众数与平均数相等，那么这组数据的中位数是（ ）(A)x=8 (B)x=9 (C)x=10 (D)x=12C3.某班50名学生身高测量结果如下： 1.10名学生的体重分别是41，48，50，53，49，50，53，51，67（单位：kg），这组数据的极差是（ ）（A）27 （B）26 （C） 25 （D）24BC该班学生身高的众数和中位数分别是( )（A）1.60,1.56 （B）1.59,1.58 （C）1.60,1.58 （D）1.60,1.60典题突破5.甲、乙两班举行电脑汉字输入比赛，参赛学生每分钟输入汉字的个数统计结果如下表： 某同学分析上表后得出如下结论：①甲、乙两班学生成绩平均水平相同；②乙班优秀的人数多于甲班优秀的人数（每分钟输入汉字≥150个为优秀）；③甲班成绩的波动比乙班大，上述结论正确的是（ ）4.如果一组数据a1，a2，…an的方差是2，那么一组新数2a1，2a2，…2an的方差是（ ）（A）2 （B）4 （C） 8 （D）16CA（A）①②③ （B）①② （C）①③ （D）②③典题突破1、为了调查某一路汽车流量，记录了30天中每天同一时段通过该路口的汽车辆数，其中4天是284辆，4天是290辆，12天是312辆，10天是314辆，那么这30天该路口同一时段通过的汽车平均数为 辆 。2、小芳测得连续5天日最低气温并整理后得出下表：由于不小心被污染了两个数据，这两个数据分别是 、 。3、某地两校联谊文艺晚会上甲、乙两个文艺节目均由10个演员表演，他们的年龄（岁）分别如下：甲节目：13 ，13，14，15，15，15，15，16，17，17乙节目：5，5，6，6，6，6，7，7，50，52（1）甲节目中演员年龄的中位数是 ；乙节目中演员年龄的众数是 。（2）两个节目中，演员年龄波动较小的是 。3064 2156甲节目中演员的年龄典题突破年收入 (万元)所占户数比 （1）填写下表 这20个家庭的年平均收入为————万元。（2）.数据中的中位数是————万元，众数是————万元。112345311.61.21.34、这是我们20个同学家一年核桃树种植收入情况，根据统计图完成以下问题：典题突破2、某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，面试包括形体和口才，笔试中包括专业水平和创新能力考察，他们的成绩（百分制）如下表（1）若公司根据经营性质和岗位要求认为：形体、口才、专业水平、创新能力按照5：5：4：6的比确定，请计算甲、乙两人各自的平均成绩，看看谁将被录取？解：（1）∴乙将被录取。典题突破(1)(2)的结果不一样说明了什么？在加权平均数中,由于权的不同,导致了结果的相异（2）若公司根据经营性质和岗位要求认为：面试成绩中形体占5%，口才占30%，笔试成绩中专业水平点35%，创新能力点30%，那么你认为该公司会录取谁？解：（2）∴甲将被录取。典题突破3、在一次数学测验中，八年级（1）班两个组的12名学生的成绩如下（单位：分）一组：109 97 83 94 65 72 87 96 59 85 78 84二组：98 81 58 74 95 100 61 73 80 94 57 96试对这两个小组的数学考试成绩作出比较和分析。解：一组的平均分x＝84.08分，中位数为84.5分，方差S2＝184.58; 二组的平均分x＝80.58分，中位数为77分，方差S2＝238.08; 因此,从平均分可看出一组整体成绩较好;从中位数可以看出一组整体成绩靠前;从方差可以看出一组同学成绩差距不大，因而一组学生成绩各方面都较好。典题突破4、在某旅游景区上山的一条小路上，有一些断断续续的台阶，如图所示，是其中的甲、乙台阶的示意图，请你用学过的统计知识回答下列问题：151616141415151118171019甲路段乙路段（1）两段台阶路有哪些相同点和不同点？解：（2）哪段台阶路走起来更舒服？为什么？（3）为方便游客行走，需要重新整修上山的小路，对于这两段台阶，在台阶数不变的情况下，请你提出合理的整修建议。解：使每个台阶的高度均为15cm，使得方差为0。解：甲台阶走起来更舒服些，因为它的台阶高度的方差小。相同点：两段台阶的平均高度相同；不同点：两段台阶的中位数、方差和极差不同。典题突破（1）求y与x之间的函数关系式；（2）如果A，B，C三种汽车的运费分别为600元/辆、800元/辆、1000元/辆，请设计一种运费最省的运输方案，并求出至少需要运费多少元？中考拓展综合运用　　这个问题难在哪里？建立函数模型　　怎样找出变量之间的关系？　　（2x+4y）+2x+21-x-y+2y+6（21-x-y）=111，　　 y=-3x+36。中考拓展　（1）求y与x之间的函数关系式；中考拓展　（2）如果A，B，C三种汽车的运费分别为600元/辆、800元/辆、1000元/辆，请设计一种运费最省的运输方案，并求出至少需要运费多少元。　　解：设总运费为w元，　　则w=600 x+800（-3x+36）+ 1000（2x-15），　　即w=200x+13800，（8≤x≤12）。　　因为w随着x的增大而增大，所以当x=8时，w最小，w的最小值为15400。　　即用A型车8辆、B型车12辆、C型车1辆运输时费用最省，最小运费为15400元。中考拓展　　（1）读题目，画图表；　　（2）标数据，做表示；　　（3）找关系，建模型；　　（4）解模型，做解释。　　在解决这个问题中，是按照怎样的步骤进行的？中考拓展　　建立函数模型的步骤：　 （1）读题目，画图表；（2）标数据，做表示；　 （3）找关系，建模型；（4）解模型，做解释。中考拓展成功的花，人们只惊慕她现时的明艳！然而当初它的芽儿，浸透了奋斗的泪泉，洒遍了牺牲的血雨。谢谢观看