第七讲 方程与零点学案

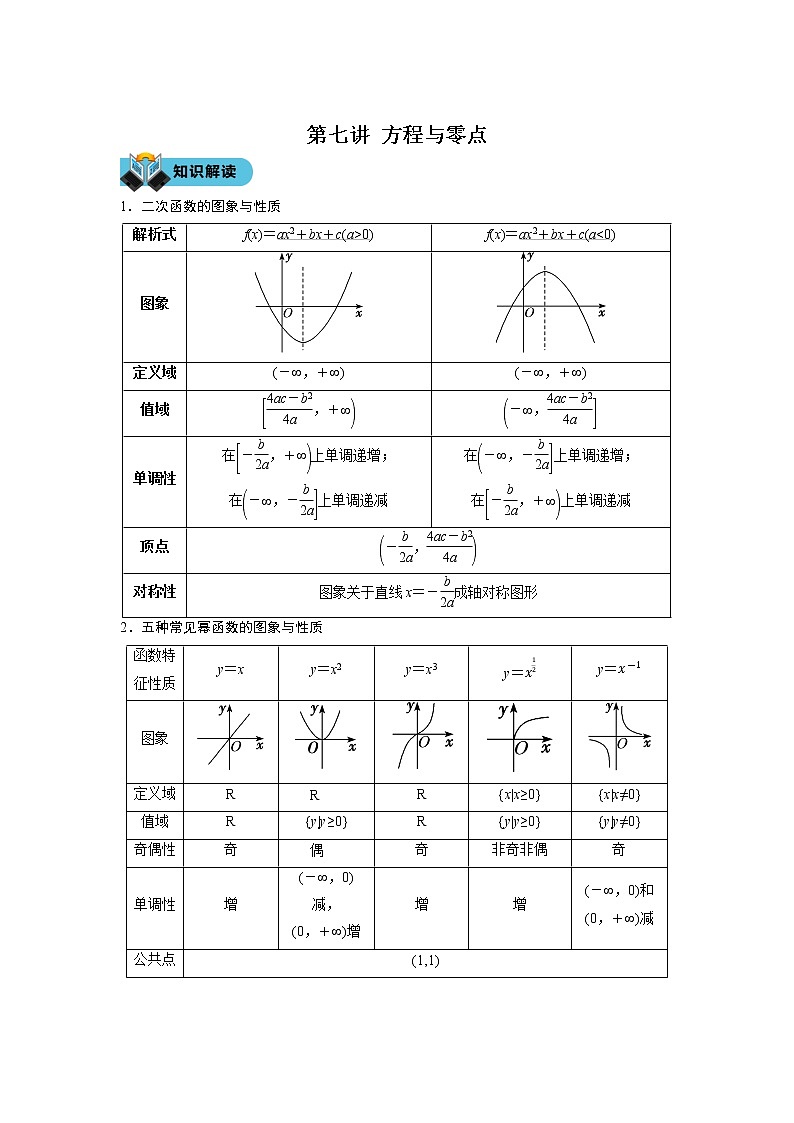
这是一份第七讲 方程与零点学案，共5页。

1．二次函数的图象与性质
2．五种常见幂函数的图象与性质
1．若二次函数y＝2x2＋bx＋c关于y轴对称，且过点(0,3)，则函数的解析式为( )
A．y＝2x2＋x＋3 B．y＝2x2＋3
C．y＝2x2＋x－3D．y＝2x2－3
2．若函数y＝x2－2tx＋3在[1，＋∞)上为增函数，则t的取值范围是( )
A．(－∞，1] B．[1，＋∞)C．(－∞，－1]D．[－1，＋∞)
3．已知函数f(x)＝ax2＋x＋5的图象在x轴上方，则a的取值范围是( )
A．eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1,20)))B．eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，－\f(1,20)))C．eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,20)，＋∞))D．eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,20)，0))
1．函数的零点
(1)函数零点的定义
把使f(x)＝0的实数x叫做函数y＝f(x)(x∈D)的零点．
(2)三个等价关系
方程f(x)＝0有实数根⇔函数y＝f(x)的图象与x轴有交点⇔函数y＝f(x)有零点．
(3)函数零点的判定(零点存在性定理)
如果函数y＝f(x)在区间[a，b]上的图象是连续不断的一条曲线，并且有f(a)·f(b)<0，那么，函数y＝f(x)在区间(a，b)内有零点，即存在c∈(a，b)，使得f(c)＝0，这个c也就是方程f(x)＝0的根．
2．二次函数y＝ax2＋bx＋c (a>0)的图象与零点的关系
1．已知函数f(x)的图象是连续不断的，且有如下对应值表：
在下列区间中，函数f(x)必有零点的区间为( )
A．(1,2) B．(2,3)C．(3,4)D．(4,5)
2．已知2是函数f(x)＝lg2(x+m),x≥22x, x<2 的一个零点，则ff4的值是________．
3*．函数f(x)＝(x－1)ln(x－2)的零点有( )
A．0个B．1个C．2个D．3个
1．已知函数f(x)＝－x2＋2ax＋1－a在x∈[0,1]时，有最大值2，则a的值为________．
2．已知函数f(x)＝x2＋2x＋1，f(x)>x＋k在区间-3,-1上恒成立，则k的取值范围为．
3．设f(x)＝ln x＋x－2，则函数f(x)的零点所在的区间为( )
A．(0,1)B．(1,2)C．(2,3)D．(3,4)
4．若aA．(a，b)和(b，c)内B．(－∞，a)和(a，b)内
C．(b，c)和(c，＋∞)内D．(－∞，a)和(c，＋∞)内
5．已知函数f(x)＝x2-2x，x≤0x+1x，x>0 则函数y＝f(x)＋3x的零点个数是( )
A．0 B．1C．2D．3
6．设函数f(x)＝eq \f(1,3)x－ln x，则函数y＝f(x)( )
A．在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,e)，1))，(1，e)内均有零点
B．在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,e)，1))，(1，e)内均无零点
C．在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,e)，1))内有零点，在区间(1，e)内无零点
D．在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,e)，1))内无零点，在区间(1，e)内有零点
7．(2018全国Ⅰ)已知函数f(x)＝ex，x≤0，lnx，x>0，g(x)＝f(x)＋x＋a.若g(x)存在2个零点，则a的取值范围是( )
A．[－1,0) B．[0，＋∞)C．[－1，＋∞)D．[1，＋∞)
8．若函数f(x)＝4x－2x－a，x∈[－1,1]有零点，则实数a的取值范围是________．
1．(安徽)下列函数中，既是偶函数又存在零点的是 ( )
A． B． C．D．
2．(山东)已知函数f(x)＝|x－2|＋1，g(x)＝kx，若方程f(x)＝g(x)有两个不相等的实根，则实数k的取值范围是( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1,2)))B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，1))C．(1，2) D．(2，＋∞)
3．(天津)设函数f(x)＝ex＋x－2，g(x)＝ln x＋x2－3.若实数a，b满足f(a)＝0，g(b)＝0，则( )
A．g(a)<04．(天津)函数的零点所在的一个区间是( )
A．(－2，－1)B．(－1，0)C．(0，1)D．(1，2)
5．(浙江)已知a，b，c∈R,函数f(x)=ax2+bx+c．若f(0)=f(4)>f(1)，则( )
A．a>0，4a+b=0B．a<0，4a+b=0 C．a>0，2a+b=0 D．a<0，2a+b=0
6．(陕西)方程在内 ( )
A．没有根 B．有且仅有一个根 C．有且仅有两个根D．有无穷多个根
7．(湖南)函数的图像与函数的图象的交点个数为( )
A．3 B．2 C．1 D．0
8．(天津)函数的零点个数为 ( )
A．1B．2C．3D．4
1．(全国)函数的图像与函数的图像所有交点的横坐标之和等于 ( )
A．2 B．4 C．6 D．8
2．(山东)已知是上最小正周期为2的周期函数，且当时，，则函数的图象在区间[0,6]上与轴的交点的个数为 ( )
A．6 B．7 C．8 D．9
3．(浙江)已知，函数，当时，不等式的解集是
_ _____．若函数恰有2个零点，则的取值范围是____．解析式
f(x)＝ax2＋bx＋c(a>0)
f(x)＝ax2＋bx＋c(a<0)
图象
定义域
(－∞，＋∞)
(－∞，＋∞)
值域
eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(4ac－b2,4a)，＋∞))
eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(4ac－b2,4a)))
单调性
在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递增；
在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递减
在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递增；
在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递减
顶点
eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(b,2a)，\f(4ac－b2,4a)))
对称性
图象关于直线x＝－eq \f(b,2a)成轴对称图形
函数特征性质
y＝x
y＝x2
y＝x3
y＝x12
y＝x-1
图象
定义域
R
eq \a\vs4\al(R)
R
{x|x≥0}
{x|x≠0}
值域
R
{y|y≥0}
R
{y|y≥0}
{y|y≠0}
奇偶性
奇
eq \a\vs4\al(偶)
奇
非奇非偶
奇
单调性
增
(－∞，0)减，
(0，＋∞)增
增
增
(－∞，0)和
(0，＋∞)减
公共点
(1,1)
Δ>0
Δ＝0
Δ<0
二次函数
y＝ax2＋bx＋c(a>0)
的图象
与x轴的交点
(x1,0)，(x2,0)
(x1,0)
无交点
零点个数
2
1
0
x
1
2
3
4
5
f(x)
－4
－2
1
4
7