2021-2022学年鲁教版（五四制）六年级上学期数学期末复习试卷（word版 含答案）

这是一份2021-2022学年鲁教版（五四制）六年级上学期数学期末复习试卷（word版 含答案），共13页。试卷主要包含了有下列结论，下列各题中去括号正确的是，下列句子中错误的是等内容，欢迎下载使用。
1．在式子，x+y，2020，﹣a，﹣3x2y，中，整式的个数（ ）
A．5个B．4个C．3个D．2个
2．已知关于x的方程x﹣a＝3x﹣14，若a为正整数时，方程的解也为正整数，则a的最大值是（ ）
A．12B．13C．14D．15
3．用四舍五入法得到的近似数1.02×104，其精确度为（ ）
A．精确到十分位B．精确到十位
C．精确到百位D．精确到千位
4．有下列结论：其中正确结论的个数是（ ）
①用一个平面去截正方体，截面可能是六边形；
②正数和负数统称为有理数；
③单项式的系数是；
④如果a＝b，那么，
A．1个B．2个C．3个D．4个
5．若x＝1是方程2x+a＝0的解，则a＝（ ）
A．1B．2C．﹣1D．﹣2
6．下列各题中去括号正确的是（ ）
A．1﹣3（x+1）＝1﹣3x﹣1
B．
C．
D．5（x﹣2）﹣2（y﹣1）＝5x﹣10﹣6y﹣2
7．下列句子中错误的是（ ）
①如果两项的字母相同，那么这两项是同类项；
②所含字母相同，并且相同字母的指数也分别相同的项叫同类项；
③系数相同的项能合并；
④系数互为相反数的同类项合并后为零．
A．①③B．②④C．①④D．②③
8．已知关于x的多项式mx2﹣mx﹣2与3x2+mx+m的和是单项式，则代数式m2﹣2m+1的值是（ ）
A．16B．﹣3C．2 或﹣3D．16 或 1
9．利用两块完全一样的长方体木块测量一张桌子的高度，首先按图①所示的方式放置，再交换两木块的位置，按图②所示的方式放置．测量的数据如图，则桌子的高度等于（ ）
A．80cmB．75cmC．70cmD．65cm
10．已知关于x的方程x﹣＝﹣1的解是非正整数，则符合条件的所有整数a的和是（ ）
A．﹣4B．﹣3C．2D．3
11．如图，正方形ABCD的边长为4，点E在AB边上．四边形EFGB也为正方形，设△AFC的面积为S，则（ ）
A．S＝6B．S＝8
C．S＝10D．S与BE长度有关
12．有一个两位数，它的十位数字与个位数字之和为5，则符合条件的两位数有（ ）
A．4个B．5个C．6个D．7个
二．填空题（共6小题，满分18分，每小题3分）
13．单项式的系数是 ，次数是 ．
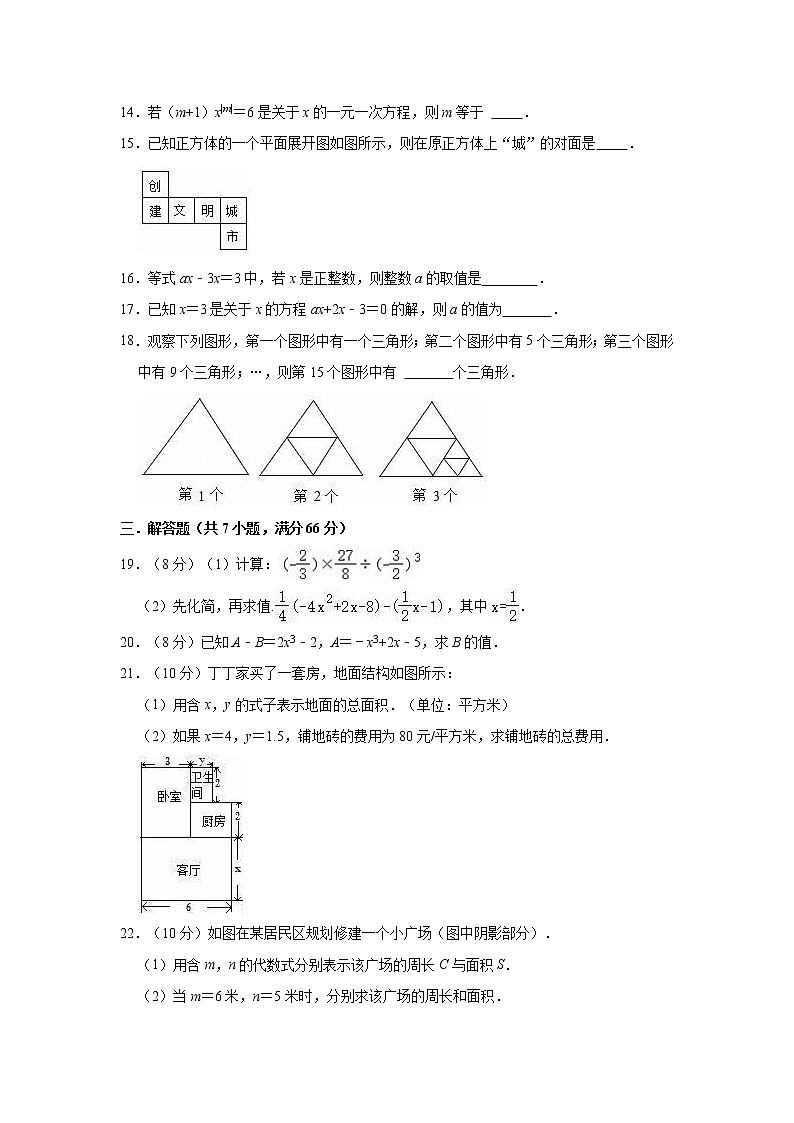
14．若（m+1）x|m|＝6是关于x的一元一次方程，则m等于 ．
15．已知正方体的一个平面展开图如图所示，则在原正方体上“城”的对面是 ．
16．等式ax﹣3x＝3中，若x是正整数，则整数a的取值是 ．
17．已知x＝3是关于x的方程ax+2x﹣3＝0的解，则a的值为 ．
18．观察下列图形，第一个图形中有一个三角形；第二个图形中有5个三角形；第三个图形中有9个三角形；…，则第15个图形中有 个三角形．
三．解答题（共7小题，满分66分）
19．（8分）（1）计算：
（2）先化简，再求值.，其中．
20．（8分）已知A﹣B＝2x3﹣2，A＝﹣x3+2x﹣5，求B的值．
21．（10分）丁丁家买了一套房，地面结构如图所示：
（1）用含x，y的式子表示地面的总面积．（单位：平方米）
（2）如果x＝4，y＝1.5，铺地砖的费用为80元/平方米，求铺地砖的总费用．
22．（10分）如图在某居民区规划修建一个小广场（图中阴影部分）．
（1）用含m，n的代数式分别表示该广场的周长C与面积S．
（2）当m＝6米，n＝5米时，分别求该广场的周长和面积．
23．（10分）将连续的偶数2，4，6，8，10…排列成如下的数表（每行6个数），用十字框框出5个数（如图）．将十字框上下左右平移，使得十字框正好框住数列中的5个数，我们发现这五个数的和总等于中间数的整数倍．设中间的数为a．
（1）则框住的5个数字之和＝ （用含a的代数式表示）．
（2）是否存在实数a，使得该十字框框住的5个数之和恰好等于2022？若存在，求出a的值；若不存在，请说明理由；
（3）十字框框住的5个数之和能等于430吗？若能，分别写出十字框框住的这5个数；若不能，请说明理由．
24．（10分）学校为奖励在艺术节系列活动中表现优秀的同学，计划购买甲、乙两种奖品．已知购买甲种奖品30件和乙种奖品25件需花费1950元，购买甲种奖品15件和乙种奖品35件需花费1650元．
（1）求甲、乙两种奖品的单价；
（2）学校计划购买甲、乙两种奖品共1800件，其中购买乙种奖品的件数不超过甲种奖品件数的2倍，学校分别购买甲、乙两种奖品多少件才能使总费用最小？最小费用是多少元？
25．（10分）如图，一个瓶子的容积为1升，瓶内装着一些溶液，当瓶子正放时，瓶内溶液的高度为20cm，倒放时，空余部分的高度为5cm（如图）．现把溶液全部倒在一个底面直径为8cm的圆柱形杯子里．求：
（1）瓶内溶液的体积．
（2）圆柱形杯子溶液的高度是多少？
参考答案与试题解析
一．选择题（共12小题，满分36分，每小题3分）
1．解：在式子，x+y，0，﹣a，﹣3x2y，中，整式的个数是：x+y，2020，﹣a，﹣3x2y，共5个．
故选：A．
2．解：方程移项合并得：﹣ x＝a﹣14，
去分母得：﹣x＝2a﹣28，
解得：x＝28﹣2a，
∵方程的解x是正整数，
∴28﹣2a＞0，
∴a＜14
则a的最大值为13，
故选：B．
3．解：近似数1.02×104的精确度是精确到百位．
故选：C．
4．解：①用一个平面去截正方体，截面与六个面均相交即可得六边形，原说法正确．
②正有理数、负有理数和零统称为有理数，原说法错误．
③单项式﹣的系数是﹣，原说法错误．
④如果a＝b，由于c2+1＞0，那么＝，原说法正确．
其中正确结论的个数是2个，
故选：B．
5．解：将x＝1代入2x+a＝0，
∴2+a＝0，
∴a＝﹣2，
故选：D．
6．解：A选项，原式＝1﹣3x﹣3，故该选项不符合题意；
B选项，原式＝1﹣x+3，故该选项符合题意；
C选项，原式＝1﹣2x+1，故该选项不符合题意；
D选项，原式＝5x﹣10﹣2y+2，故该选项不符合题意；
故选：B．
7．解：①没有强调相同字母的指数相同，故本项错误；
②正确；
③系数相同的项不一定能合并，例如m、n系数都是1，但不能合并，故本项错误；
④正确．
故选：A．
8．解：根据题意可得
mx2﹣mx﹣2+3x2+mx+m＝（m+3）x2+m﹣2为单项式，
则m+3＝0或m﹣2＝0，
m＝﹣3或m＝2，
m＝2时，m2﹣2m+1＝4﹣4+1＝1；
m＝﹣3时，m2﹣2m+1＝9+6+1＝16，
故选：D．
9．解：设长方体木块长xcm、宽ycm，桌子的高为acm，
由题意得：，
两式相加得：2a＝150，
解得：a＝75，
故选：B．
10．解：x﹣＝﹣1，
6x﹣（4﹣ax）＝2（x+a）﹣6
6x﹣4+ax＝2x+2a﹣6
6x+ax﹣2x＝2a﹣6+4
（a+4）x＝2a﹣2
x＝，
∵方程的解是非正整数，
∴≤0，
解得：﹣4＜a≤1，
当a＝﹣3时，x＝﹣8；
当a＝﹣2时，x＝﹣3；
当a＝﹣1时，x＝﹣（舍去）；
当a＝0时，x＝﹣（舍去）；
当a＝1时，x＝0；
则符合条件的所有整数a的和是﹣3﹣2+1＝﹣4．
故选：A．
11．解：设正方形EFGB的边长为a，
根据题意得：S＝a2+16+a（4﹣a）﹣a（a+4）﹣×4×4＝8．
故选：B．
12．解：设两位数个数上数字为x，则十位数上数字为y，
根据题意得：x+y＝5，
当x＝1时，y＝4；x＝2，y＝3；x＝3，y＝2；x＝4，y＝1；x＝0，y＝5；
则符合条件的两位数有5个，
故选：B．
二．填空题（共6小题，满分18分，每小题3分）
13．解：根据单项式系数的定义，单项式的系数为﹣，次数是5．
故答案为：﹣，5．
14．解：根据题意得：m+1≠0且|m|＝1，
解得：m＝1．
故答案是：1．
15．解：由正方体的表面展开图的“相间、Z端是对面”可知，
“创”与“市”是对面，
“建”与“明”是对面，
“文”与“城”是对面，
故答案为：文．
16．解：由关于x的方程ax﹣3x＝3，得
x＝．
∵x是正整数，a是整数，
∴正整数解相应为：x＝1、x＝3，
∴a的值是：6或4．
故答案为：6或4．
17．解：将x＝3代入方程得：3a+2×3﹣3＝0，
解得：a＝﹣1．
故答案为：﹣1．
18．解：第1个图形中一共有1个三角形，
第2个图形中一共有1+4＝5个三角形，
第3个图形中一共有1+4+4＝9个三角形，
…，
第n个图形中三角形的个数是1+4（n﹣1）＝（4n﹣3）个，
当n＝15时，4n﹣3＝4×15﹣3＝57，
故答案为：57．
三．解答题（共7小题，满分66分）
19．解：（1）原式＝××＝；
（2）原式＝﹣x2+x﹣2﹣x+1＝﹣x2﹣1，
当x＝时，原式＝﹣1．
20．解：∵A﹣B＝2x3﹣2，A＝﹣x3+2x﹣5，
∴B＝A﹣（2x3﹣2）
＝（﹣x3+2x﹣5）﹣（2x3﹣2）
＝﹣x3+2x﹣5﹣2x3+2
＝﹣3x3+2x﹣3，
∴B的值为﹣3x3+2x﹣3．
21．解：（1）用含x，y的式子表示地面的总面积是：
6（x+2）+2（y+3）＝6x+2y+18（平方米）
答：地面的总面积是6x+2y+18平方米．
（2）如果x＝4，y＝1.5，
80（6x+2y+18）
＝80×（6×4+2×1.5+18）
＝80×45
＝3600（元）
答：铺地砖的总费用是3600元．
22．解：（1）由图形可得：
C＝2m×2+2n×2+2n＝4m+6n；
S＝2n×2m﹣（2m﹣m﹣0.4m）n
＝4mn﹣0.6mn
＝3.4mn；
（2）当m＝6米，n＝5米时，
C＝4m+6n
＝4×6+6×5
＝24+30
＝54；
S＝3.4mn
＝3.4×6×5
＝102．
故该广场的周长是54米，面积是102平方米．
23．解：（1）根据题意可知，数a左面的数是a﹣2，右面的数是a+2，上面的数为a﹣12，下面的数为a+12，
则a+a﹣2+a+2+a﹣12+a+12＝5a，
所以这5个数的和是5a，
故答案为：5a．
（2）若存在符合条件的实数a，则5a＝2022，
解得a＝，
因为a是整数，所以a＝不符合题意，
所以不存在实数a，使得该十字框框住的5个数之和恰好等于2022．
（3）不能，理由如下：
若十字框框住的5个数之和能等于430，
则5a＝430，
解得a＝86，
而数表最左边一列数字的第n个数为2+12（n﹣1）＝12n﹣10，
当n＝8时，12n﹣10＝86，
因为86这个数在最左边一列中，
所以86不能作为十字框的正中间一个数，
所以十字框框住的5个数之和不能等于430．
24．解：（1）设甲种奖品的单价为x元/件，乙种奖品的单价为y元/件，
依题意，得：，
解得：．
答：甲种奖品的单价为40元/件，乙种奖品的单价为30元/件．
（2）设购买甲种奖品m件，则购买乙种奖品（1800﹣m）件，设购买两种奖品的总费用为w，
∵购买乙种奖品的件数不超过甲种奖品件数的2倍，
∴1800﹣m≤2m，
∴m≥600．
依题意，得：w＝40m+30（1800﹣m）＝10m+54000，
∵10＞0，
∴w随m值的增大而增大，
∴当学习购买600件甲种奖品、1200件乙种奖品时，总费用最小，最小费用是60000元．
25．解：（1）设瓶内溶液的体积为x升，则空余部分的体积为x升，
依题意，得：x+x＝1，
解得：x＝0.8．
答：瓶内溶液的体积为0.8升．
（2）0.8×1000÷[π×（8÷2）2]＝（cm）．
答：圆柱形杯子溶液的高度是cm．