

山东省济宁市2021-2022学年八年级上学期 数学期末模拟检测(word版 含答案)
展开2021—2022学年第一学期期末检测
八年级数学试题
第I卷(选择题 30分)
一、选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
1.将下列长度的三条线段首尾相连,其中能组成三角形的是
A.5,6,10 B.2,5,8
C.4,5,9 D.3,4,8
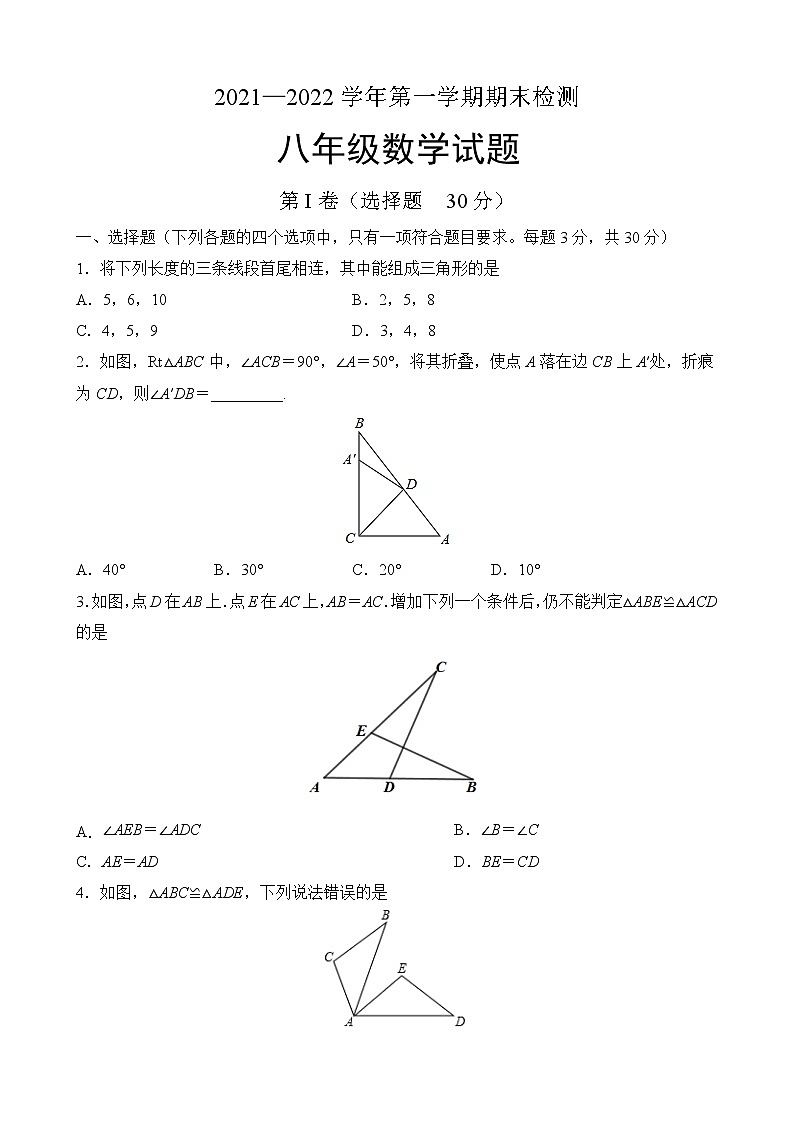
2.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=_________.
A.40° B.30° C.20° D.10°
3.如图,点D在AB上.点E在AC上,AB=AC.增加下列一个条件后,仍不能判定△ABE≌△ACD的是
A.∠AEB=∠ADC B.∠B=∠C
C.AE=AD D.BE=CD
4.如图,△ABC≌△ADE,下列说法错误的是
A.BC=DE B.AB⊥DE C.∠CAE=∠BAD D.∠B=∠D
5.下列图形是轴对称图形的是
A. B. C. D.
6.如图,在△ABC中,AB=AC=9,点E在边AC上,AE的中垂线交BC于点D,若∠ADE=∠B,CD=3BD,则CE等于
A.3 B.2 C. D.
7.下列计算中错误的是
A. B.
C. D.
8.对于算式,下列说法不正确的是
A.能被2016整除 B.能被2017整除
C.不能被2018整除 D.能被2015整除
9.下列四个分式的运算中,其中运算结果正确的有
①;②;③;④ .
A.3个 B.2个 C.1个 D.0个
10.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),以下五个结论正确的个数是
①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤.
A.2 B.3 C.4 D.5
第II卷(非选择题 70分)
二、填空题
11.若△ABC的边AB、BC的长是方程组的解,设边AC的长为m,则m的取值范围是_____.
12.如图,已知△ABC中,∠C=90°,AD平分∠BAC,且D是BC的中点.若BC=6,则点D到AB边的距离为_______.
13.若点P(2,4)与点B(x,y)关于y轴对称,那么x-y的值为_______.
14.我们定义=ad﹣bc,例如=2×5﹣3×4=10﹣12=﹣2.如果x、y均为有理数,并且满足=0,那么x+y的值为 ___.
15.某工程需要在规定日期内完成,如果甲工程队单独做,恰好如期成:如果乙工程队单独做,则超过规定日期3天,现在甲、乙两队合做2天,剩下的由乙队独做,恰好在规定日期完成,求规定日期.如果设规定日期为x天,根据题意列方程得___________________.
三、解答题(共55分)
16.(6分)(1)因式分解:. (2)解方程:=1.
18.(6分)先化简,再求值:,其中,.
19.(6分)如图所示,在正方形网格上有一个,、、在格点上.
(1)画关于直线的对称图形(不写画法,保留作图痕迹);
(2)若网格上的每个小正方形的边长都为,求的面积.
20.(8分)如图①,AD平分∠BAC,AE⊥BC,∠B=38°,∠C=64°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,∠B=α,∠C=β(α<β),请用α、β 的代数式表示∠DFE.
21.(7分)如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,则FC的长度为 m.
22.(9分)如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
23.(13分)如图,在△ABC中,AB=AC,∠B=50°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.
(1)当∠BDA=100°时,∠BAD= °,∠DEC= °;
(2)当DC=AB时,△ABD和△DCE是否全等?请说明理由;
(3)在点D的运动过程中,是否存在△ADE是等腰三角形的情形?若存在,请直接写出此时∠BDA的度数,若不存在,请说明理由.
【参考答案】
一、选择题(每题3分,共30分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | D | D | B | C | A | B | D | C | C |
二、填空题(每题3分,共15分)
11.3<m<9 12.3 13.-6 14.4 15.
三、解答题(共55分)
16.(1)原式=(x2-2xy+y2)-25
=(x-y)2-52
=(x-y+5)(x-y-5).
(2)x=6
17.解:原式
,
当,时,原式.
18.(1)如图所示,即为所求:
(2)由题意得:.
19.解:(1),,
,
平分,
,
,
,
,
.
(2),,
,
平分,
,
,
,
,
.
20.(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(ASA);
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10-3-3=4m.
21.解:(1)∵AB=AC,
∴∠C=∠ABC,
∵∠C=36°,
∴∠ABC=36°,
∵D为BC的中点,
∴AD⊥BC,
∴∠BAD=90°﹣∠ABC=90°﹣36°=54°.
(2)∵BE平分∠ABC,
∴∠ABE=∠EBC,
又∵EF∥BC,
∴∠EBC=∠BEF,
∴∠EBF=∠FEB,
∴BF=EF.
22.解:(1)∵在△BAD中,∠B=∠50°,∠BDA=100°,∠ADE=50°,
∴∠BAD=180°﹣∠B﹣∠BDA=30°,∠EDC=180°﹣∠BDA﹣∠ADE=30°,
∵AB=AC,
∴∠B=∠C=50°,
∴∠DEC=180°﹣∠C﹣∠EDC=180°﹣50°﹣30°=100°,
故答案为:30,100;
(2)∵∠B=∠C=50°,
∴∠DEC+∠EDC=180°﹣∠C=130°,
又∵∠ADE=50°,
∴∠ADB+∠EDC=180°﹣∠ADE =130°,
∴∠ADB=∠DEC,
在△ABD和△DCE中,
∴△ABD≌△DCE(AAS).
(3)当△ADE是等腰三角形时,∠BDA的度数为100°或115°,
①当ED=EA时,
∴∠DAE=∠EDA=50°,
∴∠BDA=∠C+∠DAE=100°;
②当DA=DE时,
∴∠DAE=∠DEA=(180°﹣∠ADE)=65°,
∴∠BDA=∠C+∠DAE=115°,
③当AD=AE时,
∠ADE=∠AED=50°
∵∠C=50°
∠AED是△EDC的外角
∴∠AED>∠C,与∠AED=50°矛盾
所以此时不成立;
综上所述:当△ADE是等腰三角形时,∠BDA的度数为100°或115°.
山东省济宁市曲阜师范大附属实验学校2023-2024学年九上数学期末检测模拟试题含答案: 这是一份山东省济宁市曲阜师范大附属实验学校2023-2024学年九上数学期末检测模拟试题含答案,共8页。试卷主要包含了分式方程的根是等内容,欢迎下载使用。
2023-2024学年山东省济宁市任城区八上数学期末检测模拟试题含答案: 这是一份2023-2024学年山东省济宁市任城区八上数学期末检测模拟试题含答案,共6页。试卷主要包含了下列各数组中,不是勾股数的是等内容,欢迎下载使用。
2022—2023学年山东省济宁市八年级上册数学期末检测模拟试卷: 这是一份2022—2023学年山东省济宁市八年级上册数学期末检测模拟试卷,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












