高中数学人教版新课标A选修2-1第三章 空间向量与立体几何综合与测试课后复习题

这是一份高中数学人教版新课标A选修2-1第三章 空间向量与立体几何综合与测试课后复习题，共9页。试卷主要包含了被一平面所截得到的， 如图，在直三棱柱中，等内容，欢迎下载使用。
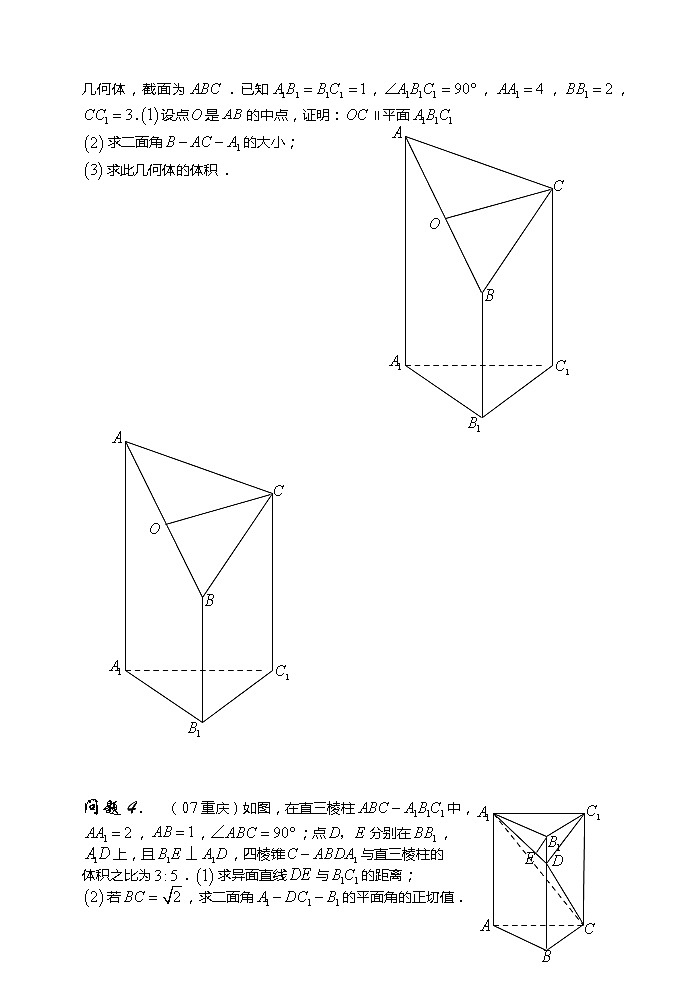
课题：立体几何综合问题教学目标：能够熟练解决折叠与展开问题；立体几何内部的综合问题；立体几何与数学其它分支的综合问题.教学重点：如何解决综合问题.（一） 主要知识： 折叠问题的计算与证明：一定要关注“变量”和“不变量”在证明和计算中的应用:折叠时位于棱同侧的位置关系和数量关系不变;位于棱两侧的位置关系与数量关系变，折前折后的图形结合起来使用.（二）典例分析： 问题1． （江西）如图，在直三棱柱中，底面为直角三角形，,，，是上一动点，则的最小值是                   问题2．将如图所示的直角梯形（图中所示数字为对应线段长度）沿直线折成直二面角，连结部分线段后围成一个空间几何体，如图所示，求异面直线与所成角的大小；求二面角的大小；这五个点在同一球面上，求该球的表面积.                                     问题3．（江西）右图是一个直三棱柱（以为底面）被一平面所截得到的几何体，截面为．已知，，，，.设点是的中点，证明：∥平面求二面角的大小；求此几何体的体积 .                      问题4． （重庆）如图，在直三棱柱中，，，；点分别在，上，且，四棱锥与直三棱柱的体积之比为．求异面直线与的距离；若，求二面角的平面角的正切值．
                         （三）课后作业： 将正方形折成正四棱柱的侧面，正方形的对角线被折成折线，则为定值                有一个长方体形的水泥构件，其中，，，现在小蚂蚁要从点沿表面到放有食物的点，则小蚂蚁需走的最短路线长为                            已知体积为的正三棱锥的外接球的半径是，且满足，则其外接球的表面积是         （用含及数字作答，不能含）         如果是线段上一点，则；类比到平面的情形：若是内一点，有；类比到空间的情形：若是四面体内一点，则有                                三棱锥的条棱中，其中条棱的长都是，则第条棱长的取值范围是                          （届高三湖北八校月考）如图，所在的平面和四边形所在的平面垂直，且，，，，，，则点在平面内的轨迹是圆的一部分               椭圆的一部分双曲线的一部分           抛物线的一部分            （届高三安徽省江南十校联考）如图，已知正方体的棱长为，长为的线段的一个端点在棱上运动，点在正方形内运动，则中点的轨迹的面积为                   四面体的一条棱长为，其它各棱长为，若将四面体的体积表示为的函数，则函数的单调递减区间为        （四）走向高考： （湖南）棱长为的正方体的个顶点都在球的表面上，分别是棱，的中点，则直线被球截得的线段长为               ．（安徽文）把边长为的正方形沿对角线折成直二面角，折成直二面角后，在四点所在的球面上，与两点之间的球面距离为               （江西）如图，正方体的棱长为，过点作平面的垂线，垂足为点，则以下命题中，错误的命题是点是的垂心垂直平面的延长线经过点直线和所成角为    （天津）如图，在斜三棱柱中，，，，侧面与底面所成的二面角为，分别是棱、的中点.求与底面所成的角；证明：∥平面；求经过四点的球的体积.