2022届上海市浦东新区高三一模数学试卷

浦东新区2021学年度第一学期期末教学质量检测

高三数学试卷          

考生注意：1、本试卷共21道试题，满分150分，答题时间120分钟；

2、请在答题纸上规定的地方解答，否则一律不予评分 .

一、填空题（本大题满分54分）本大题共有12题，1-6题每题4分，7-12题每题5分．考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分或5分，否则一律得零分．

1．已知复数（为虚数单位），则           .

2．函数的反函数为，则           .

3．已知，则的值为           .

4．已知集合 ，，则=           .

5．底面半径长为2，母线长为3的圆柱的体积为           .

6．三阶行列式中，元素2的代数余子式的值为           .

7．数列的通项公式为，则           .

8．方程的解为           .

9. 已知函数，若对任意的恒成立，则实数的取值范围是           .

10．某学校要从6名男生和4名女生中选出3人担任进博会志愿者，则所选3人中男女生都有的概率为           .（用数字作答）

11．已知、、，点是圆上的动点，则的取值范围是           .

12．已知实数满足，则的取值范围是           .

二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案．考生必须在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．

13．已知直线在平面上，则“直线”是“直线”的        （     ）

（A）充分非必要条件             （B）必要非充分条件

（C）充要条件                 （D）既非充分又非必要条件

14．的二项展开式中第4项是                                  （     ）

（A）       （B）         （C）        （D）

15．若方程表示双曲线，则此双曲线的虚轴长等于           （     ）

（A）        （B）        （C）           （D）

16．函数，零点的个数不可能是             （     ）

（A）12个        （B）13个   （C）14个         （D）15个

三、解答题（本大题满分76分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．

17．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.

已知三棱锥中，、、两两互相垂直，且长度均为1．

（1）求三棱锥的全面积；

（2）若点为的中点，求与平面所成角的大小．

（结果用反三角函数值表示）

18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.

已知函数，．

（1）判断函数的奇偶性，并说明理由；

（2）若函数，写出函数的单调递增区间并用定义证明．

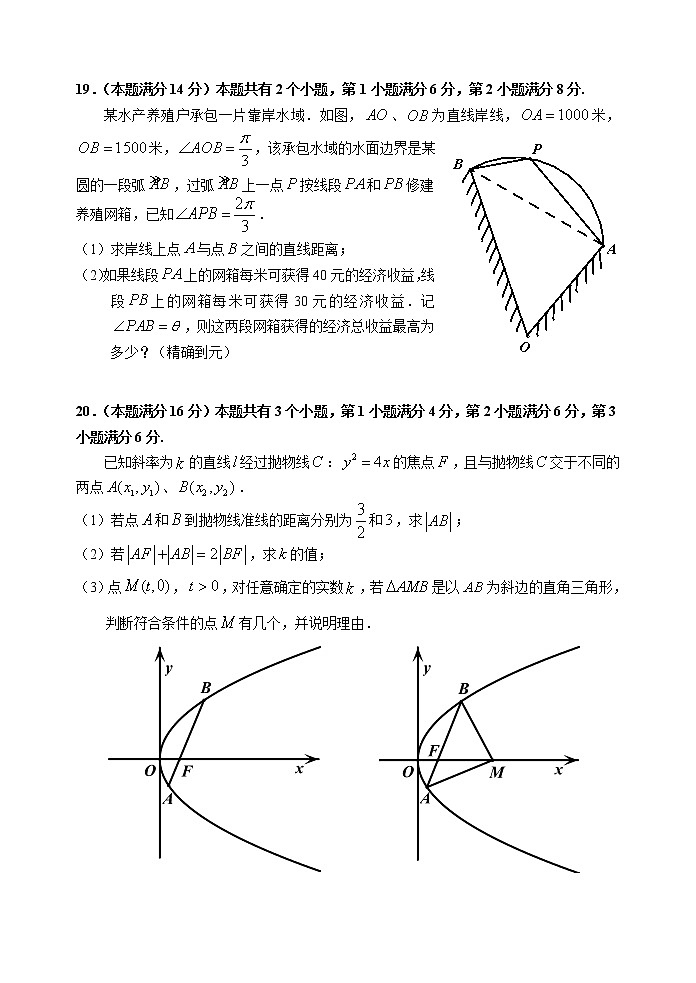
19．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.

某水产养殖户承包一片靠岸水域．如图，、为直线岸线，米，米，，该承包水域的水面边界是某

圆的一段弧，过弧上一点按线段和修建

养殖网箱，已知．

（1）求岸线上点与点之间的直线距离；

（2）如果线段上的网箱每米可获得40元的经济收益，线段上的网箱每米可获得30元的经济收益．记，则这两段网箱获得的经济总收益最高为多少？（精确到元）

20．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分.

已知斜率为的直线经过抛物线：的焦点，且与抛物线交于不同的两点、．

（1）若点和到抛物线准线的距离分别为和，求；

（2）若，求的值；

（3）点，，对任意确定的实数，若是以为斜边的直角三角形，判断符合条件的点有几个，并说明理由．

21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.

已知数列，若存在使得数列是递减数列，则称数列是“型数列”．

（1）判断数列是否为“0型数列”；

（2）若等比数列的通项公式为（），，其前项和为，且{}是“型数列”，求的值和的取值范围；

（3）已知，数列满足，（）．若存在，使得

是“型数列”，求的取值范围，并求出所有满足条件的（用表示）．

浦东新区2021学年度第一学期期末教学质量检测

高三数学答案              2021.12

1．    2． 4    3．    4．    5．    6． 3

7．2    8．    9.    10．    11．    12．

13． B   14． C   15．B   16． D

17．解：（1）三棱锥的全面积

…………………….6分

（2）取的中点，连接和，

因为平面，在平面上，

所以，又因为

所以平面，

所以是与平面所成角；……………………….10分

因为，，

所以， ，

所以与平面所成角的大小为．………………………14分

18．解：（1）当时，，

定义域为， 任选，都有，

所以时函数为偶函数；………………………………….3分

当，

则；

时函数既非奇函数又非偶函数；………………………….6分

（2）函数的单调递增区间为．

证明：，

任取且   ……………………….8分

……………10分

由于，则；由于，则；

所以，即．  …………………………12分

函数的单调递增区间为．      ………………………………….14分

19． 解：（1）

，

岸线上点与点之间的直线距离为米．…………………………….6分

（2）△中，，

，，（）………………8分

设两段网箱获得的经济总收益为元，则

……………………….12分

当，即时，……………………….13分

（元）

所以两段网箱获得的经济总收益最高约为55076元．……………………….14分

20． 解：（1）根据抛物线定义，，∴.     ……………4分.     

（2）直线的方程为，

，   ，      ………………5分

                           ………………6分

 ，             

 ，

    ， …………8分

，                          ………………9分

代入（5）得：，

或，   ∴ .            ………………10分

（3）∵ 是以为斜边的直角三角形，

∴ ，，                         ………………11分

, ,

即，

，

（或者），

∴ ，，    ………………14分

， ，方程仅有一个正实数解，

存在一个满足条件的点.                             ………………16分.

21．解：（1），因此是的……………………………………………4分

（2）若，，不存在使得数列是递减数列，不是“型数列”；

若，，因为为递增数列，对于任意，存在，

当时，，递增，不存在，不是“型数列”；

若，，取，，递减；

综上，．…………………………….……10分

（3）（i）若，则，，. 此时若存在使得是型数列，则，从而且，矛盾………..12分

（ii）当时，首先证明（）. 用反证法.（猜出答案给2分）…14分

由题意，此时，，. 因此，若存在，使得，则.

假设为使得的最小正整数，则，故，而，与的最小性矛盾. 故（），从而对一切成立.

据此，可解得. 故当时，，即：为递减数列. 于是为型数列…………………….16分

再证明是唯一解. 用反证法.

假设存在使得是型数列.

若，则由得，当时，. 故，不是递减数列，从而不是型数列. 同理可证时也不是型数列……………………..18分

综上，，相应的.