数学七年级下册第四章 三角形1 认识三角形教课课件ppt

这是一份数学七年级下册第四章 三角形1 认识三角形教课课件ppt，共21页。PPT课件主要包含了教学目标，新课导入，新知探究，从三角形的一个顶点，三角形的高，锐角三角形的三条高，问题1，问题2，探究交流，直角三角形的三条高等内容，欢迎下载使用。

1.掌握三角形的高的概念.（重点）2.掌握三角形的高的画法.3.掌握钝角三角形的两短边上高的画法.（难点）
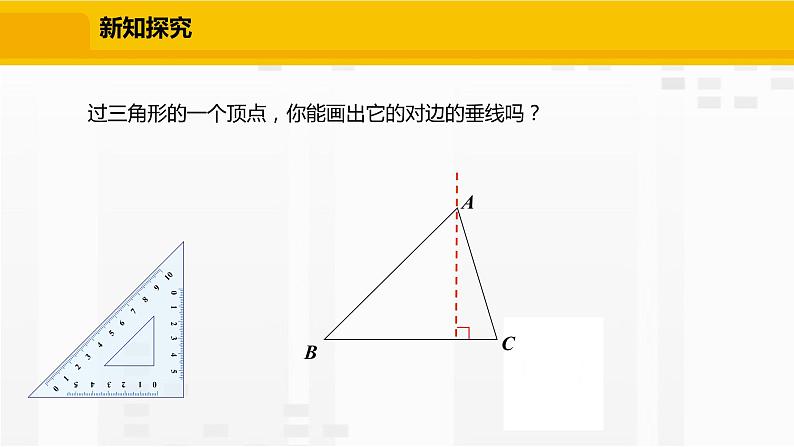
你还记得怎样“过一点画已知直线的垂线”吗？
过三角形的一个顶点，你能画出它的对边的垂线吗？
如图，线段AD是BC边上的高.
向它的对边所在的直线作垂线，
顶点与垂足之间的线段，叫做三角形的高.
注意：标明垂直的记号和垂足的字母 .
练习：画出下列三角形的高 .
注意：直角三角形的两条高与两条直角边重合 .
钝角三角形有两条高在三角形外部，画高时需要延长对应的两条边 .
高的叙述方法（如图）：有三种
②AD⊥BC,垂足为D.
③点D在BC上，且∠BDA=∠CDA=90°.
①AD是△ABC的高.
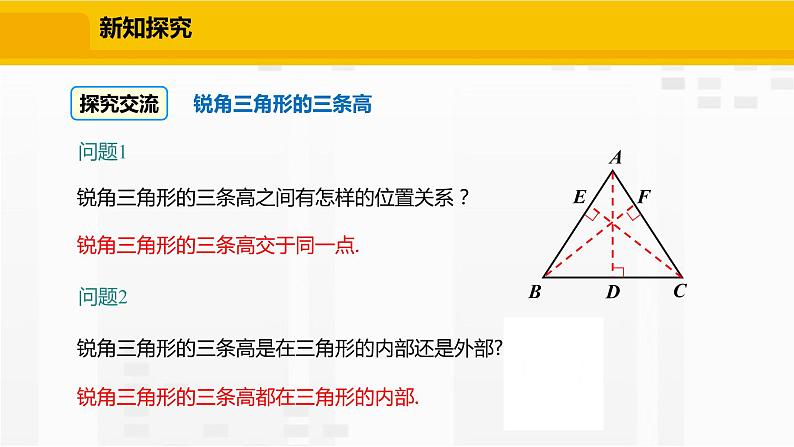
锐角三角形的三条高之间有怎样的位置关系？
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
锐角三角形的三条高是在三角形的内部还是外部?
(1)说出直角三角形的三条高：
直角边BC上的高是______;
直角边AB上的高是 ;
(2)它们有怎样的位置关系？
斜边AC上的高是_______.
直角三角形的三条高交于直角顶点.
问题4(1) 钝角三角形的三条高交于一点吗？
(2)它们所在的直线交于一点吗？
钝角三角形的三条高不交于一点.
钝角三角形的三条高所在的直线交于一点.
三条高所在直线的交点的位置
三角形的三条高所在直线交于一点 .
1、在△ABC中，∠A＝ ∠B＝ ∠ACB，CD是△ABC的高，CE是∠ACB的平分线，求∠DCE的度数．
解析：根据已知条件用∠A表示出∠B和∠ACB，利用三角形的内角和求出∠A，再求出∠ACB，∠ACD，最后根据角平分线的定义求出∠ACE，即可求得∠DCE的度数．
比例关系可考虑用方程思想求角度.
解：因为∠A＝ ∠B＝ ∠ACB，设∠A＝x，所以∠B＝2x，∠ACB＝3x.因为∠A＋∠B＋∠ACB＝180°，所以x＋2x＋3x＝180°，得x＝30°，所以∠A＝30°，∠ACB＝90°.因为CD是△ABC的高，所以∠ADC＝90°，所以∠ACD＝180°－90°－30°＝60°.因为CE是∠ACB的平分线，所以∠ACE＝ ×90°＝45°，所以∠DCE＝∠ACD－∠ACE＝60°－45°＝15°.
解：∠A+∠BFC=180°.理由： 因为CD⊥AB于点D，BE⊥AC于点E， 所以∠BEA=∠BDF=90°， 所以∠ABE+∠A=90°， ∠ABE+∠DFB=90°. 所以∠A=∠DFB. 因为∠DFB+∠BFC=180°， 所以∠A+∠BFC=180°.
2、如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，CD，BE相交于点F，∠A与∠BFC又有什么关系？为什么？
注意：作高时要标明垂直的记号和垂足的字母 .
1、三角形的三条高相交于一点，此一点定在（ ） A．三角形的内部 B． 三角形的外部 C． 三角形的一条边上 D．不能确定
2、下列各组图形中，哪一组图形中的AD是△ABC的高（ ）
A B C D
3、如图，在△ABC中，∠ACB＝90°，CD是AB边上的高. 若∠A＝50°，则∠DCB的度数是( )A．50° B．45° C．40° D．25°
4、如图所示，在△ABC中，AB＝AC＝10，BC＝12，AD⊥BC于点D，且AD＝8. 若点P在边AC上移动，求BP的最小值.
解：根据垂线段最短，可知当BP⊥AC时，BP有最小值．
代入数值，可解得BP＝8×12÷10=9.6 .