专题05 14.2乘法公式 - 期末复习专题训练 2021-2022学年人教版数学八年级上册

这是一份专题05 14.2乘法公式 - 期末复习专题训练 2021-2022学年人教版数学八年级上册，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
专题05 : 2021年人教新版八年级（上册）14.2乘法公式 - 期末复习专题训练
一、选择题（共10小题）
1．下列各式中，不能用平方差公式计算的是（　　）
A．（x﹣y）（﹣x+y） B．（﹣x+y）（﹣x﹣y）
C．（﹣x﹣y）（x﹣y） D．（x+y）（﹣x+y）
2．将图甲中阴影部分的小长方形变换到图乙位置，根据两个图形的面积关系可以得到一个关于a、b的恒等式为（　　）

A．（a﹣b）2＝a2﹣2ab+b2 B．（a+b）2＝a2+2ab+b2
C．（a+b）（a﹣b）＝a2﹣b2 D．a（a﹣b）＝a2﹣ab
3．已知x2﹣8x+a可以写成一个完全平方式，则a可为（　　）
A．4 B．8 C．16 D．﹣16
4．计算（﹣a﹣b）2等于（　　）
A．a2+b2 B．a2﹣b2 C．a2+2ab+b2 D．a2﹣2ab+b2
5．下列多项式相乘，不能用平方差公式计算的是（　　）
A．（2x﹣3y）（3y﹣2x） B．（﹣2x+3y）（﹣2x﹣3y）
C．（x﹣2y）（2y+x） D．（x+3y）（x﹣3y）
6．利用图形中面积的等量关系可以得到某些数学公式．例如，根据图甲，我们可以得到两数和的平方公式：（a+b）2＝a2+2ab+b2．你根据图乙能得到的数学公式是（　　）

A．（a+b）（a﹣b）＝a2﹣b2 B．（a﹣b）2＝a2﹣2ab+b2
C．a（a+b）＝a2+ab D．a（a﹣b）＝a2﹣ab
7．如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个长方形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（　　）
A．（a﹣b）2＝a2﹣2ab+b2 B．（a+b）2＝a2+2ab+b2
C．a2﹣b2＝（a+b）（a﹣b） D．a2+ab＝a（a+b）
8．若x2+2（m﹣3）x+1是完全平方式，x+n与x+2的乘积中不含x的一次项，则nm的值为（　　）
A．﹣4 B．16 C．4或16 D．﹣4或﹣16
9．已知a+b＝﹣5，ab＝﹣4，则a2﹣ab+b2＝（　　）
A．29 B．37 C．21 D．33
10．如图，有三种规格的卡片共9张，其中边长为a的正方形卡片4张，边长为b的正方形卡片1张，长，宽分别为a，b的长方形卡片4张．现使用这9张卡片拼成一个大的正方形，则这个大正方形的边长为（　　）

A．2a+b B．4a+b C．a+2b D．a+3b
二、填空题（共5小题）
11．已知a﹣b＝2，那么a2﹣b2﹣4b的值为　 　．
12．若a+b＝5，a﹣b＝3，则a2﹣b2＝　 　．
13．若x2+2（m﹣3）x+16是完全平方式，则m的值等于　 　．
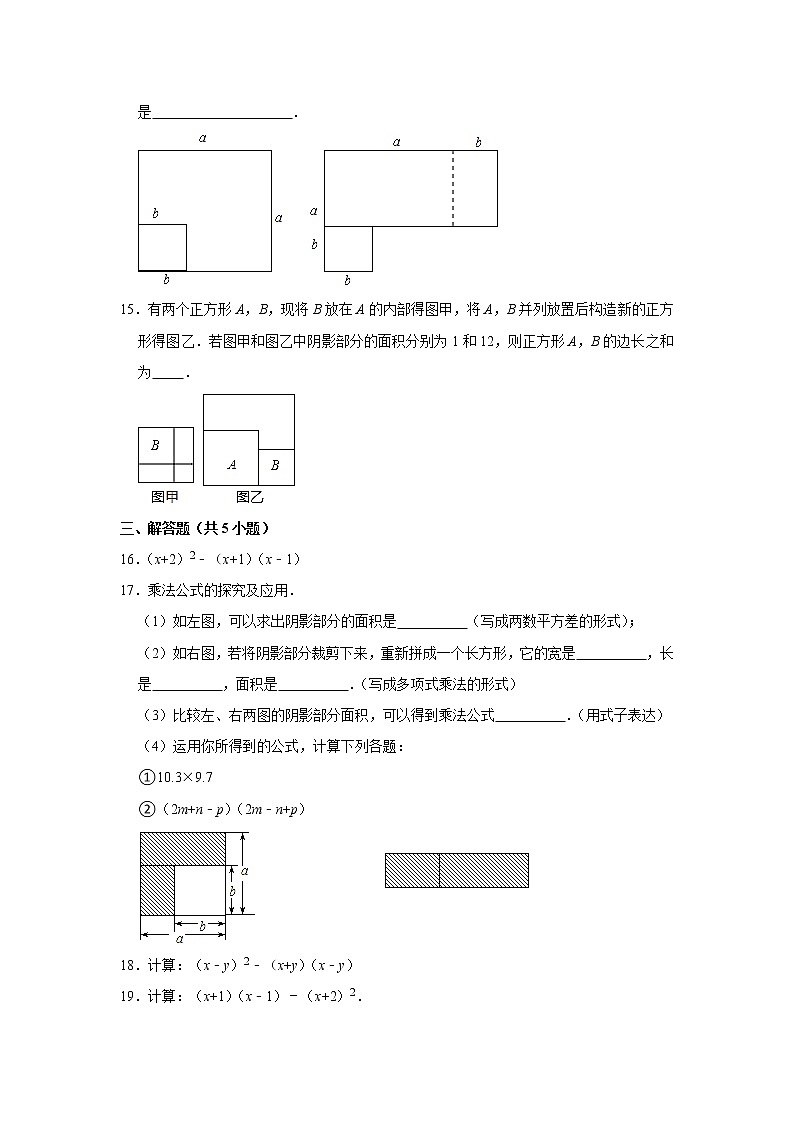
14．如图，在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），再把剩余的部分剪拼成一个矩形，通过计算图形（阴影部分）的面积，验证了一个等式是　 　．

15．有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的边长之和为　 　．

三、解答题（共5小题）
16．（x+2）2﹣（x+1）（x﹣1）
17．乘法公式的探究及应用．
（1）如左图，可以求出阴影部分的面积是　 　（写成两数平方差的形式）；
（2）如右图，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是　 　，长是　 　，面积是　 　．（写成多项式乘法的形式）
（3）比较左、右两图的阴影部分面积，可以得到乘法公式　 　．（用式子表达）
（4）运用你所得到的公式，计算下列各题：
①10.3×9.7
②（2m+n﹣p）（2m﹣n+p）

18．计算：（x﹣y）2﹣（x+y）（x﹣y）
19．计算：（x+1）（x﹣1）﹣（x+2）2．
20．在学习“乘法公式”时，育红中学七（1）班数学兴趣小组在活动课上进行了这样的操作：作两条互相垂直的线段AB和CD．把大正方形分成四部分（如图所示）．
观察发现
（1）请用两种不同的方法表示图形的面积，得到一个等量关系：　 　．
类比操作
（2）请你作一个图形验证：（x+y）（2x+y）＝2x2+3xy+y2．
延伸运用
（3）若AB+CD＝14，图中阴影部分的面积和为13，求xy的值．


专题05 : 2021年人教新版八年级（上册）14.2乘法公式 - 期末复习专题训练
参考答案与试题解析
一、选择题（共10小题）
1．下列各式中，不能用平方差公式计算的是（　　）
A．（x﹣y）（﹣x+y） B．（﹣x+y）（﹣x﹣y）
C．（﹣x﹣y）（x﹣y） D．（x+y）（﹣x+y）
【解答】解：A、（x﹣y）（﹣x+y）＝﹣（x﹣y）（x﹣y），含y的项符号相同，含x的项符号相同，不能用平方差公式计算，故本选项正确；
B、含x的项符号相同，含y的项符号相反，能用平方差公式计算，故本选项错误；
C、含y的项符号相同，含x的项符号相反，能用平方差公式计算，故本选项错误；
D、含y的项符号相同，含x的项符号相反，能用平方差公式计算．故本选项错误；
故选：A．
2．将图甲中阴影部分的小长方形变换到图乙位置，根据两个图形的面积关系可以得到一个关于a、b的恒等式为（　　）

A．（a﹣b）2＝a2﹣2ab+b2 B．（a+b）2＝a2+2ab+b2
C．（a+b）（a﹣b）＝a2﹣b2 D．a（a﹣b）＝a2﹣ab
【解答】解：图甲面积＝（a﹣b）（a+b），
图乙面积＝a（a﹣b+b）﹣b×b＝a2﹣b2，
∵两图形的面积相等，
∴关于a、b的恒等式为：（a+b）（a﹣b）＝a2﹣b2．
故选：C．

3．已知x2﹣8x+a可以写成一个完全平方式，则a可为（　　）
A．4 B．8 C．16 D．﹣16
【解答】解：∵x2﹣8x+a可以写成一个完全平方式，
∴则a可为：16．
故选：C．
4．计算（﹣a﹣b）2等于（　　）
A．a2+b2 B．a2﹣b2 C．a2+2ab+b2 D．a2﹣2ab+b2
【解答】解：（﹣a﹣b）2＝a2+2ab+b2．
故选：C．
5．下列多项式相乘，不能用平方差公式计算的是（　　）
A．（2x﹣3y）（3y﹣2x） B．（﹣2x+3y）（﹣2x﹣3y）
C．（x﹣2y）（2y+x） D．（x+3y）（x﹣3y）
【解答】解：（2x﹣3y）（3y﹣2x）不能利用平方差公式计算，
故选：A．
6．利用图形中面积的等量关系可以得到某些数学公式．例如，根据图甲，我们可以得到两数和的平方公式：（a+b）2＝a2+2ab+b2．你根据图乙能得到的数学公式是（　　）

A．（a+b）（a﹣b）＝a2﹣b2 B．（a﹣b）2＝a2﹣2ab+b2
C．a（a+b）＝a2+ab D．a（a﹣b）＝a2﹣ab
【解答】解：左上角正方形的面积＝（a﹣b）2，
还可以表示为a2﹣2ab+b2，
∴（a﹣b）2＝a2﹣2ab+b2．
故选：B．
7．如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个长方形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（　　）
A．（a﹣b）2＝a2﹣2ab+b2 B．（a+b）2＝a2+2ab+b2
C．a2﹣b2＝（a+b）（a﹣b） D．a2+ab＝a（a+b）
【解答】解：第一个图形的阴影部分的面积＝a2﹣b2；
第二个图形是长方形，则面积＝（a+b）（a﹣b）．
则a2﹣b2＝（a+b）（a﹣b）．
故选：C．
8．若x2+2（m﹣3）x+1是完全平方式，x+n与x+2的乘积中不含x的一次项，则nm的值为（　　）
A．﹣4 B．16 C．4或16 D．﹣4或﹣16
【解答】解：∵x2+2（m﹣3）x+1是完全平方式，（x+n）（x+2）＝x2+（n+2）x+2n不含x的一次项，
∴m﹣3＝±1，n+2＝0，
解得：m＝4，n＝﹣2，此时原式＝16；
m＝2，n＝﹣2，此时原式＝4，
则原式＝4或16，
故选：C．
9．已知a+b＝﹣5，ab＝﹣4，则a2﹣ab+b2＝（　　）
A．29 B．37 C．21 D．33
【解答】解：把a+b＝5两边平方得：（a+b）2＝a2+b2+2ab＝25，
将ab＝﹣4代入得：a2+b2＝33，
则a2﹣ab+b2＝33﹣（﹣4）＝37．
故选：B．
10．如图，有三种规格的卡片共9张，其中边长为a的正方形卡片4张，边长为b的正方形卡片1张，长，宽分别为a，b的长方形卡片4张．现使用这9张卡片拼成一个大的正方形，则这个大正方形的边长为（　　）

A．2a+b B．4a+b C．a+2b D．a+3b
【解答】解：由题可知，9张卡片总面积为4a2+4ab+b2，
∵4a2+4ab+b2＝（2a+b）2，
∴大正方形边长为2a+b．
故选：A．
二、填空题（共5小题）
11．已知a﹣b＝2，那么a2﹣b2﹣4b的值为　4　．
【解答】解：∵a﹣b＝2，
∴a＝2+b，
∴那么a2﹣b2﹣4b的
＝（2+b）2﹣b2﹣4b
＝4+4b+b2﹣b2﹣4b
＝4，
故答案为：4．
12．若a+b＝5，a﹣b＝3，则a2﹣b2＝　15　．
【解答】解：∵a+b＝5，a﹣b＝3，
∴a2﹣b2
＝（a+b）（a﹣b）
＝5×3
＝15，
故答案为：15．
13．若x2+2（m﹣3）x+16是完全平方式，则m的值等于　7或﹣1　．
【解答】解：∵x2+2（m﹣3）x+16是完全平方式，
∴2（m﹣3）x＝±2•x•4，
解得：m＝7或﹣1，
故答案为：7或﹣1．
14．如图，在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），再把剩余的部分剪拼成一个矩形，通过计算图形（阴影部分）的面积，验证了一个等式是　a2﹣b2＝（a+b）（a﹣b）　．

【解答】解：左边图形中，阴影部分的面积＝a2﹣b2，
右边图形中，阴影部分的面积＝（a+b）（a﹣b），
∵两个图形中的阴影部分的面积相等，
∴a2﹣b2＝（a+b）（a﹣b）．
故答案为：a2﹣b2＝（a+b）（a﹣b）．
15．有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的边长之和为　5　．

【解答】解：设正方形A，B的边长分别为a，b．
由题意
由②得到ab＝6，
∴（a+b）2＝（a﹣b）2+4ab＝1+24＝25，
∵a+b＞0，
∴a+b＝5，
故答案为5．
三、解答题（共5小题）
16．（x+2）2﹣（x+1）（x﹣1）
【解答】解：（x+2）2﹣（x+1）（x﹣1）
＝x2+4x+4﹣x2+1
＝4x+5．
故答案为：4x+5．
17．乘法公式的探究及应用．
（1）如左图，可以求出阴影部分的面积是　a2﹣b2　（写成两数平方差的形式）；
（2）如右图，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是　a﹣b　，长是　a+b　，面积是　（a+b）（a﹣b）　．（写成多项式乘法的形式）
（3）比较左、右两图的阴影部分面积，可以得到乘法公式　（a+b）（a﹣b）＝a2﹣b2　．（用式子表达）
（4）运用你所得到的公式，计算下列各题：
①10.3×9.7
②（2m+n﹣p）（2m﹣n+p）

【解答】解：（1）利用大正方形面积减去小正方形面积即可求出：a2﹣b2；

（2）它的宽是 a﹣b，长是 a+b，面积是（a+b）（a﹣b）；

（3）根据题意得出：（a+b）（a﹣b）＝a2﹣b2；

（4）①10.3×9.7
＝（10+0.3）（10﹣0.3）
＝100﹣0.09
＝99.91；
②（2m+n﹣p）（2m﹣n+p）
＝[2m+（n﹣p）][2m﹣（n﹣p）]
＝4m2﹣（n﹣p）2
＝4m2﹣n2﹣p2+2np．
18．计算：（x﹣y）2﹣（x+y）（x﹣y）
【解答】解：原式＝（x2﹣2xy+y2）﹣（x2﹣y2），
＝x2﹣2xy+y2﹣x2+y2，
＝﹣2xy+2y2．
19．计算：（x+1）（x﹣1）﹣（x+2）2．
【解答】解：（x+1）（x﹣1）﹣（x+2）2
＝x2﹣1﹣x2﹣4x﹣4
＝﹣4x﹣5．
20．在学习“乘法公式”时，育红中学七（1）班数学兴趣小组在活动课上进行了这样的操作：作两条互相垂直的线段AB和CD．把大正方形分成四部分（如图所示）．
观察发现
（1）请用两种不同的方法表示图形的面积，得到一个等量关系：　（x+y）2＝x2+2xy+y2　．
类比操作
（2）请你作一个图形验证：（x+y）（2x+y）＝2x2+3xy+y2．
延伸运用
（3）若AB+CD＝14，图中阴影部分的面积和为13，求xy的值．

【解答】解：（1）由图知，大正方形的边长为x+y，则大正方形的面积为（x+y）2，
∵大正方形的面积为各部分面积和：x2+2xy+y2，
∴（x+y）2＝x2+2xy+y2，
故答案为（x+y）2＝x2+2xy+y2；

（2）如图所示，


（3）∵AB+CD＝14，
∴x+y＝7，
∵阴影部分的面积和为13，
∴x2+y2＝13，
∵（x+y）2＝x2+2xy+y2，
∴72＝13+2xy，
∴xy＝18．