浙江省宁波市南三县2021-2022学年八年级上学期期末数学模拟试卷（word版 含答案）

2021-2022学年浙江省宁波市南三县八年级（上）期末数学模拟试卷

一、选择题（每小题3分，共30分）

1．有两根长度分别为，的木棒，下面为第三根的长度，则可围成一个三角形框架的是　　

A． B． C． D．

2．在命题 ①若那么②当时，是正比例函数；③时，那么；④三角形的外角和是；其中假命题是　　

A．①② B．①④ C．①②③④ D．②③④

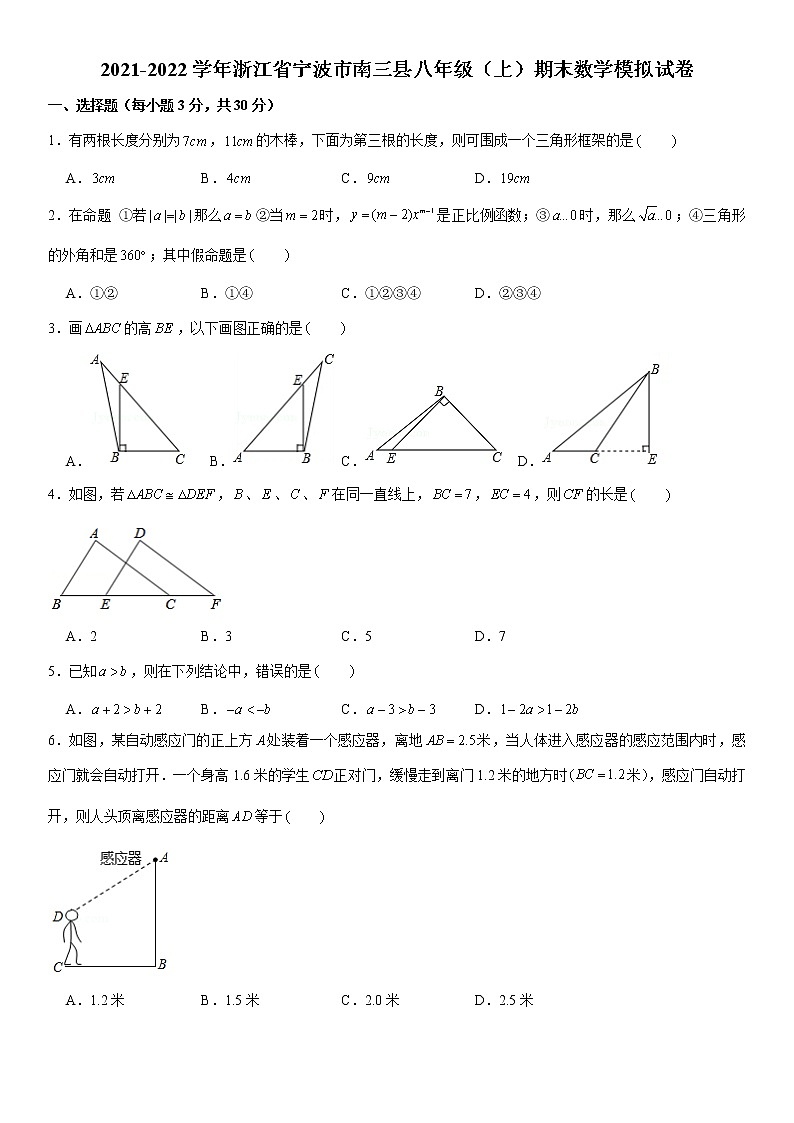
3．画的高，以下画图正确的是　　

A．   B． C．  D．

4．如图，若，、、、在同一直线上，，，则的长是　　

A．2 B．3 C．5 D．7

5．已知，则在下列结论中，错误的是　　

A． B． C． D．

6．如图，某自动感应门的正上方处装着一个感应器，离地米，当人体进入感应器的感应范围内时，感应门就会自动打开．一个身高1.6米的学生正对门，缓慢走到离门1.2米的地方时米），感应门自动打开，则人头顶离感应器的距离等于　　

A．1.2米 B．1.5米 C．2.0米 D．2.5米

7．已知关于的一次函数图象经过点、，则，的大小关系为　　

A． B． C． D．

8．韩日“世界杯”期间，重庆球迷一行56人从旅馆乘出租车到球场为中国队加油，现有、两个出租车队，队比队少3辆车，若全部安排乘队的车，每辆坐5人，车不够，每辆坐6人，有的车未满；若全部安排队的车，每辆车4人，车不够，每辆坐5人，有的车未满，则队有出租车　　

A．11辆 B．10辆 C．9辆 D．8辆

9．若关于的不等式组无解，则的取值范围是　　

A． B． C． D．

10．四个形状大小相同的等腰三角形按如图所示方式摆放，已知，，若点落在的延长线上，则图中阴影部分的面积为　　

A． B． C． D．

二、填空题（每小题4分，共24分）

11．在圆、正六边形、正方形、等边三角形中，对称轴的条数最少的图形是　　．

12．如图，围棋盘放在某平面直角坐标系内，已知黑棋（甲的坐标为，黑棋（乙的坐标为，则白棋（甲的坐标是　　．

13．如图，中，，，请依据尺规作图的作图痕迹，计算　 　

14．如图，在中，，，，是边上的中线，则　　．

15．若点到两坐标轴的距离相等，则点的坐标是 　　．

16．如图，直线交轴于点，为轴正半轴上一点，轴交直线于点，，交于点，记的面积为，的面积为，当时，的长为　　．

三．解答题（共9小题，17·18每题4分，19~21每题6分，22题8分，23~24每题10分，25题12分.）

17．解不等式：，并把它的解集在数轴上表示出来．

18．若关于的不等式的解集与相同，求的取值范围．

19．如图，点、、、在一条直线上，，，．

（1）求证：；

（2）求证：．

20．已知点．

（1）若点在轴上，求的值．

（2）若点到两坐标轴的距离相等，求点的坐标．

21．小凡与小光从学校出发到距学校5千米的图书馆看书，途中小凡从路边超市买了一些学习用品，如图反映了他们俩人离开学校的路程（千米）与时间（分钟）的关系，请根据图象提供的信息回答问题：

（1）　　先出发，先出发了 　　分钟；

（2）当　　分钟时，小凡与小光在去图书馆的路上相遇；

（3）小凡与小光从学校到图书馆的平均速度各是多少千米小时？

（不包括停留的时间）

22．如图，在等腰中，，，点关于直线的对称点为点，连接与的延长线交于点．在上取点，使得，连接．

（1）依题意补全图形；

（2）求证：．

23．某学校为了满足疫情防控需求，决定购进、两种型号的口罩若干盒，若购进型口罩10盒，型口罩5盒，共需1000元，若购进型口罩4盒，型口罩3盒，共需550元．

（1）求、两种型号的口罩每盒各需多少元？

（2）若该学校决定购进这两种型号的口罩共计200盒，并要求购进型口罩的盒数不超过型口罩盒数的4倍，请为该学校设计出最省钱的购买方案，并说明理由．

24．阅读材料：

通过一次函数的学习，小明知道：当已知直线上两个点的坐标时，可以用待定系数法，求出这个一次函数的表达式．

有这样一个问题：直线的表达式为，若直线与直线关于轴对称，求直线的表达式．

下面是小明的解题思路，请补充完整．

第一步：求出直线与轴的交点的坐标，与轴的交点的坐标；

第二步：在平面直角坐标系中，作出直线；

第三步：求点关于轴的对称点的坐标；

第四步：由点，点的坐标，利用待定系数法，即可求出直线的表达式．

小明求出的直线的表达式是　 　．

请你参考小明的解题思路，继续解决下面的问题：

（1）若直线与直线关于直线对称，则直线的表达式是　 　；

（2）若点在直线上，将直线绕点顺时针旋转．得到直线，求直线的表达式．

25．如图，在直角坐标系中，直线与直线相交于点，与轴的交点为．

（1）求的值，以及直线的解析式；

（2）若有一动点从原点出发，沿轴正半轴向点运动，过作直线轴，直线与的另一边交点记为，点关于直线作轴对称变换，对称点为，

①当时，求点的坐标；

②连接，若为直角三角形，则此时的的长为　　（直接写出答案）．

2021-2022学年浙江省宁波市南三县八年级（上）期末数学模拟试卷

参考答案与试题解析

一、选择题（每小题3分，共30分）

1．有两根长度分别为，的木棒，下面为第三根的长度，则可围成一个三角形框架的是　　

A． B． C． D．

【解答】解：依题意得：，

即，适合．

故选：．

2．在命题 ①若那么②当时，是正比例函数；③时，那么；④三角形的外角和是；其中假命题是　　

A．①② B．①④ C．①②③④ D．②③④

【解答】解：①若那么，是假命题，符合题意；

②当时，此时，故不是正比例函数，是假命题符合题意；

③时，那么，是真命题；

④三角形的外角和是，是真命题；

故选：．

3．画的高，以下画图正确的是　　

A． B． 

C． D．

【解答】解：画的高，即过点作对边所在直线的垂线段，

故选：．

4．如图，若，、、、在同一直线上，，，则的长是　　

A．2 B．3 C．5 D．7

【解答】解：，，

，

，

故选：．

5．已知，则在下列结论中，错误的是　　

A． B． C． D．

【解答】解：、，，故正确，不符合题意．

、，．故正确，不符合题意．

、，，故正确，不符合题意．

、，，．故错误，符合题意．

故选：．

6．如图，某自动感应门的正上方处装着一个感应器，离地米，当人体进入感应器的感应范围内时，感应门就会自动打开．一个身高1.6米的学生正对门，缓慢走到离门1.2米的地方时米），感应门自动打开，则人头顶离感应器的距离等于　　

A．1.2米 B．1.5米 C．2.0米 D．2.5米

【解答】解：如图，过点作于点，

米，米，米，

（米．

在中，由勾股定理得到：（米

故选：．

7．已知关于的一次函数图象经过点、，则，的大小关系为　　

A． B． C． D．

【解答】解：，

，

值随值的增大而增大．

又，

．

故选：．

8．韩日“世界杯”期间，重庆球迷一行56人从旅馆乘出租车到球场为中国队加油，现有、两个出租车队，队比队少3辆车，若全部安排乘队的车，每辆坐5人，车不够，每辆坐6人，有的车未满；若全部安排队的车，每辆车4人，车不够，每辆坐5人，有的车未满，则队有出租车　　

A．11辆 B．10辆 C．9辆 D．8辆

【解答】解：设队有出租车辆，队有辆．

依题意可得；化简得，

解得，

为整数，

．

故选：．

9．若关于的不等式组无解，则的取值范围是　　

A． B． C． D．

【解答】解：关于的不等式组无解，

，

故选：．

10．四个形状大小相同的等腰三角形按如图所示方式摆放，已知，，若点落在的延长线上，则图中阴影部分的面积为　　

A． B． C． D．

【解答】解：连接交于，连接．

，

，

，

是等腰直角三角形，

，

，，共线，

，

，

，

，

，

，

，，设，则，

在中，，

，

，

菱形的面积，

阴影部分的面积

故选：．

二、填空题（每小题4分，共24分）

11．在圆、正六边形、正方形、等边三角形中，对称轴的条数最少的图形是　等边三角形　．

【解答】解：在圆、正六边形、正方形、等边三角形中，对称轴的条数最少的图形是等边三角形，

故答案为：等边三角形．

12．如图，围棋盘放在某平面直角坐标系内，已知黑棋（甲的坐标为，黑棋（乙的坐标为，则白棋（甲的坐标是　　．

【解答】解：如图：

白棋（甲的坐标是，

故答案为：．

13．如图，中，，，请依据尺规作图的作图痕迹，计算　75　

【解答】解：，，

，

由作法可知，是的平分线，

，

由作法可知，是线段的垂直平分线，

，

，

，

故答案为：75．

14．如图，在中，，，，是边上的中线，则　6　．

【解答】解：，，，

由勾股定理得，，

是边上的中线，

，

故答案为6．

15．若点到两坐标轴的距离相等，则点的坐标是 　或　．

【解答】解：点到两坐标轴的距离相等，

，

或，

解得或，

时，，，

时，，，

点的坐标为或．

故答案为：或．

16．如图，直线交轴于点，为轴正半轴上一点，轴交直线于点，，交于点，记的面积为，的面积为，当时，的长为　6　．

【解答】解：设点的坐标为，则点的坐标为，

直线，

当时，，

即点的坐标为，

，

，

即，

，

解得，（舍去），

，

故答案为：6．

三．解答题（共9小题，17·18每题4分，19~21每题6分，22题8分，23~24每题10分，25题12分.）

17．解不等式：，并把它的解集在数轴上表示出来．

【解答】解：去分母得，，

去括号得，，

移项、合并同类项得，，

把的系数化为1得，．

在数轴上表示此不等式的解集如下：

18．若关于的不等式的解集与相同，求的取值范围．

【解答】解：

解得；

与解集相同，

解得．

19．如图，点、、、在一条直线上，，，．

（1）求证：；

（2）求证：．

【解答】解：（1），，

，

，

又，

．

（2），

，

．

20．已知点．

（1）若点在轴上，求的值．

（2）若点到两坐标轴的距离相等，求点的坐标．

【解答】解：（1）点在轴上，

，

解得：；

（2）点到两坐标轴的距离相等，

，

或，

解得：或，

或．

21．小凡与小光从学校出发到距学校5千米的图书馆看书，途中小凡从路边超市买了一些学习用品，如图反映了他们俩人离开学校的路程（千米）与时间（分钟）的关系，请根据图象提供的信息回答问题：

（1）　小凡　先出发，先出发了 　　分钟；

（2）当　　分钟时，小凡与小光在去图书馆的路上相遇；

（3）小凡与小光从学校到图书馆的平均速度各是多少千米小时？

（不包括停留的时间）

【解答】解：（1）观察两函数图象，发现：小凡先出发，比小光先出发了10分钟．

故答案为：小凡；10；

（2）小光的速度为：（千米分钟），

小光所走的路程为3千米时，用的时间为：（分钟），

当（分钟）时，小凡与小光在去图书馆的路上相遇，

故答案为：34；

（3）小凡的平均速度为：（千米小时），

小光的平均速度为：（千米小时）．

22．如图，在等腰中，，，点关于直线的对称点为点，连接与的延长线交于点．在上取点，使得，连接．

（1）依题意补全图形；

（2）求证：．

【解答】（1）解：如图，

（2）证明：连接，如图，

点，关于直线对称，

垂直平分，

，，

，

，

，

，，

在和中，

，

，

．

23．某学校为了满足疫情防控需求，决定购进、两种型号的口罩若干盒，若购进型口罩10盒，型口罩5盒，共需1000元，若购进型口罩4盒，型口罩3盒，共需550元．

（1）求、两种型号的口罩每盒各需多少元？

（2）若该学校决定购进这两种型号的口罩共计200盒，并要求购进型口罩的盒数不超过型口罩盒数的4倍，请为该学校设计出最省钱的购买方案，并说明理由．

【解答】解：（1）设购进型口罩每盒需元，型口罩每盒需元，

依题意，得：，

解得：，

答：型口罩每盒需25元，型口罩每盒需150元；

（2）设购进盒型口罩，则购进盒型口罩，

依题意，得：，

解得：．

设该学校购进这批口罩共花费元，则．

，

随的增大而减小，

又，且为整数，

当时，取得最小值，此时．

最省钱的购买方案为：购进160盒型口罩，40盒型口罩．

24．阅读材料：

通过一次函数的学习，小明知道：当已知直线上两个点的坐标时，可以用待定系数法，求出这个一次函数的表达式．

有这样一个问题：直线的表达式为，若直线与直线关于轴对称，求直线的表达式．

下面是小明的解题思路，请补充完整．

第一步：求出直线与轴的交点的坐标，与轴的交点的坐标；

第二步：在平面直角坐标系中，作出直线；

第三步：求点关于轴的对称点的坐标；

第四步：由点，点的坐标，利用待定系数法，即可求出直线的表达式．

小明求出的直线的表达式是　　．

请你参考小明的解题思路，继续解决下面的问题：

（1）若直线与直线关于直线对称，则直线的表达式是　 　；

（2）若点在直线上，将直线绕点顺时针旋转．得到直线，求直线的表达式．

【解答】解：直线的表达式为，

直线与轴的交点的坐标为，与轴的交点的坐标为，

点关于轴的对称点的坐标为．

设直线的解析式为，

则，解得，

直线的表达式为：．

故答案为：；

（1），，

、两点的坐标关于直线的对称点分别为，，

设直线的解析式为，

则，解得，

直线的表达式为：．

故答案为：；

（2）过点作直线，交轴于点，作轴于点．

点在直线上，

，

，

，，

．

设，则，，，

由勾股定理得：，

解得：

．

设直线的表达式

把，代入得：

直线的表达式．

25．如图，在直角坐标系中，直线与直线相交于点，与轴的交点为．

（1）求的值，以及直线的解析式；

（2）若有一动点从原点出发，沿轴正半轴向点运动，过作直线轴，直线与的另一边交点记为，点关于直线作轴对称变换，对称点为，

①当时，求点的坐标；

②连接，若为直角三角形，则此时的的长为　1.5或　（直接写出答案）．

【解答】解：（1）将代入得；．

点的坐标为．

设直线的解析式为，将点、的坐标代入得：，

解得：，．

直线的解析式为．

（2）①当点在上时．

将代入得；，

点的坐标为．

直线的解析式为．

点与点关于对称，

点的坐标为．

当点在上时．

将代入得，

点的坐标为．

直线的解析式为．

点与点关于对称，

点的坐标为．

②点、，

．

当时．

直线的一次项系数，

．

．

点的横坐标为．

将时，代入得：．

．

当时，，

点的横坐标为3．

点的横坐标为1.5．

将代入得：．

．

故答案为：1.5或．