四川省成都市2021-2022学年八年级上学期期末数学模拟试题五（word版 含答案）

这是一份四川省成都市2021-2022学年八年级上学期期末数学模拟试题五（word版 含答案），共26页。
2021-2022学年成都市八年级上学期期末数学模拟试题五
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）下列各数中，是无理数的是（　　）
A． B． C． D．3.1415
2．（3分）下列各组线段不能构成直角三角形的是（　　）
A．2，3，4 B．3，4，5 C．1，1， D．6，8，10
3．（3分）﹣64的立方根是（　　）
A．﹣4 B．8 C．﹣4和4 D．﹣8和8
4．（3分）若直线y＝kx+b经过第二、三、四象限，则直线y＝﹣bx+k不经过（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．（3分）在直角坐标系xOy中，点A（a，3）与B（﹣1，b）关于y轴对称，则a，b的值分别为（　　）
A．a＝1，b＝3 B．a＝﹣1，b＝﹣3 C．a＝﹣1，b＝3 D．a＝1，b＝﹣3
6．（3分）若是关于x，y的二元一次方程1﹣ay＝3x的一组解，则a的值为（　　）
A．﹣5 B．﹣1 C．2 D．7
7．（3分）已知点P（2a+6，4+a）在第二象限，则a的取值范围是（　　）
A．﹣4＜a＜﹣3 B．a＜﹣3 C．a＞﹣3 D．a＞﹣4
8．（3分）下列命题是真命题的个数为（　　）
①两条直线被第三条直线所截，内错角相等．
②三角形的内角和是180°．
③在同一平面内，平行于同一条直线的两条直线平行．
④相等的角是对顶角．
⑤两点之间，线段最短．
A．2 B．3 C．4 D．5
9．（3分）一工坊用铁皮制作糖果盒，每张铁皮可制作盒身20个，或制作盒底30个，一个盒身与两个盒底配成一套糖果盒．现有35张铁皮，设用x张制作盒身，y张制作盒底，恰好配套制成糖果盒．则下列方程组中符合题意的是（　　）
A． B．
C． D．
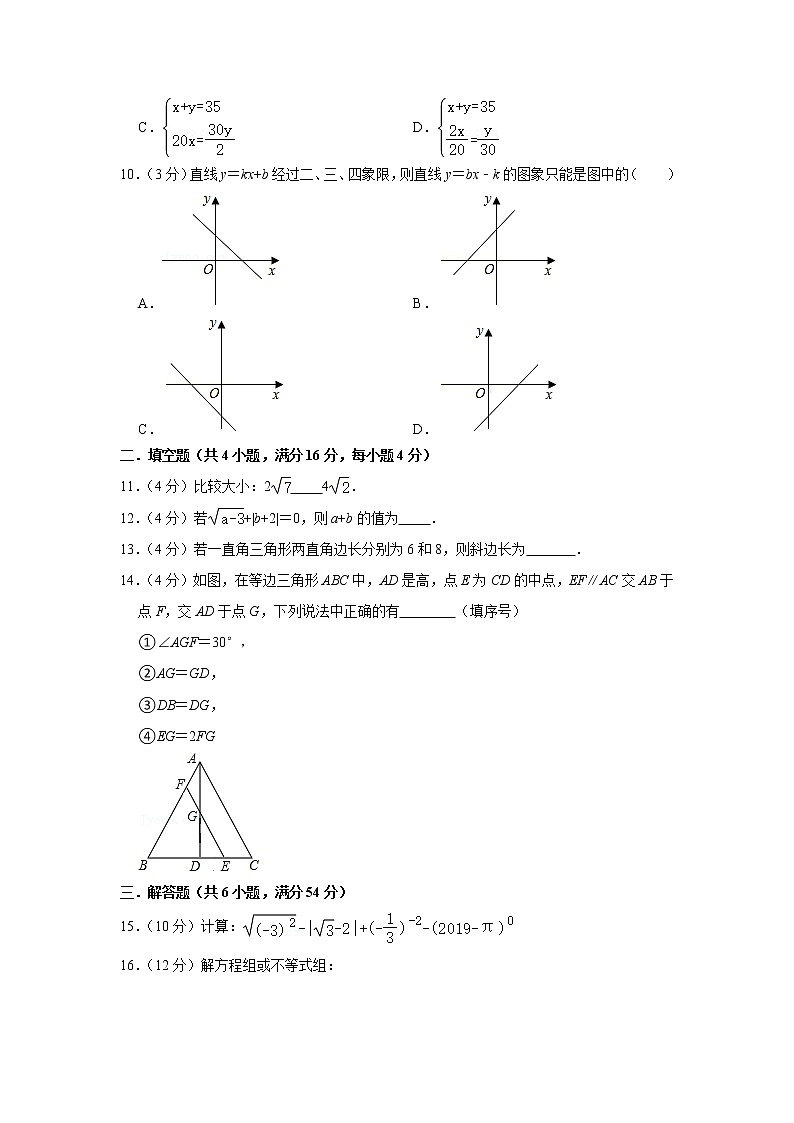
10．（3分）直线y＝kx+b经过二、三、四象限，则直线y＝bx﹣k的图象只能是图中的（　　）
A． B．
C． D．
二．填空题（共4小题，满分16分，每小题4分）
11．（4分）比较大小：2　 　4．
12．（4分）若+|b+2|＝0，则a+b的值为　 　．
13．（4分）若一直角三角形两直角边长分别为6和8，则斜边长为　 　．
14．（4分）如图，在等边三角形ABC中，AD是高，点E为CD的中点，EF∥AC交AB于点F，交AD于点G，下列说法中正确的有　 　（填序号）
①∠AGF＝30°，
②AG＝GD，
③DB＝DG，
④EG＝2FG

三．解答题（共6小题，满分54分）
15．（10分）计算：
16．（12分）解方程组或不等式组：
（1）解方程组；
（2）解不等式组：并把解集在数轴上表示出来．
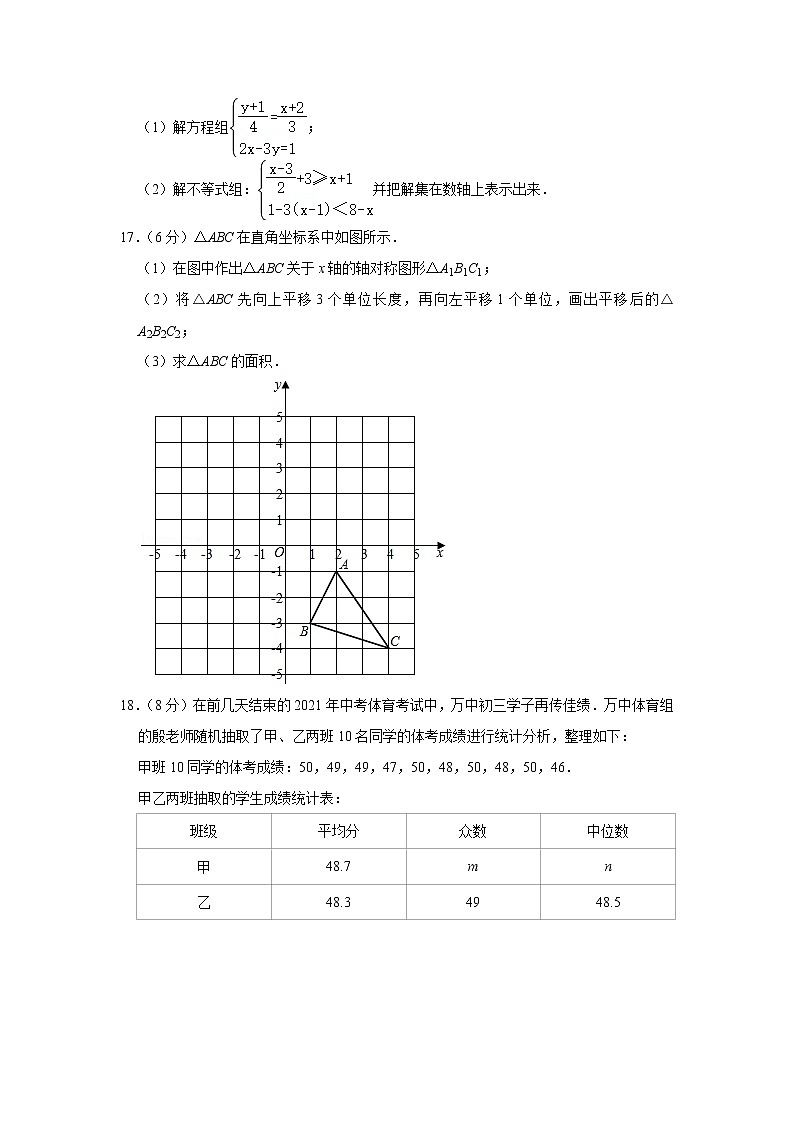
17．（6分）△ABC在直角坐标系中如图所示．
（1）在图中作出△ABC关于x轴的轴对称图形△A1B1C1；
（2）将△ABC先向上平移3个单位长度，再向左平移1个单位，画出平移后的△A2B2C2；
（3）求△ABC的面积．

18．（8分）在前几天结束的2021年中考体育考试中，万中初三学子再传佳绩．万中体育组的殷老师随机抽取了甲、乙两班10名同学的体考成绩进行统计分析，整理如下：
甲班10同学的体考成绩：50，49，49，47，50，48，50，48，50，46．
甲乙两班抽取的学生成绩统计表：
班级
平均分
众数
中位数
甲
48.7
m
n
乙
48.3
49
48.5

根据以上信息，解答下列问题：
（1）填空：上述表格中，m＝　 　，n＝　 　
（2）根据以上数据，你认为甲、乙两班中哪个班的体考成绩更好？请说明理由（一条即可）．
（3）若万州中学初2021级约有1300人参加体考，请估计48分及以上的同学共有多少人？
19．（8分）如图，直线y＝﹣x+b与x轴，y轴分别交于点A，点B，与函数y＝kx的图象交于点M（1，2）．
（1）求k，b的值，并结合图象直接写出不等式0≤﹣x+b≤kx的解集；
（2）在x轴上有一点P，过点P作x轴的垂线，分别交函数y＝﹣+b和y＝kx的图象于点C，点D．若2CD＝OB，则点P的坐标为　 　．

20．（10分）（1）如图1，等腰△ABC和等腰△ADE中，∠BAC＝∠DAE＝90°，B，E，D三点在同一直线上，求证：∠BDC＝90°；
（2）如图2，等腰△ABC中，AB＝AC，∠BAC＝90°，D是△ABC外一点，且∠BDC＝90°，求证：∠ADB＝45°；
（3）如图3，等边△ABC中，D是△ABC外一点，且∠BDC＝60°，
①∠ADB的度数；
②DA，DB，DC之间的关系．

四．填空题（共5小题，满分20分，每小题4分）
21．（4分）若y＝，则xy＝　 　．
22．（4分）一次函数y＝kx+4的图象上有一点P（2，n），将点P向右平移1个单位，再向下平移2个单位得到点Q，若点Q也在该函数的图象上，则n＝　 　．
23．（4分）关于x的不等式组有且只有4个整数解，则常数m的取值范围是　 　．
24．（4分）教材上曾让同学们探索过线段的中点坐标：在平面直角坐标系中，若两点A（x1，y1）、B（x2，y2），所连线段AB的中点是M，则M的坐标为（，），例如：点A（1，2）、点B（3，6），则线段AB的中点M的坐标为（，），即M（2，4）请利用以上结论解决问题：在平面直角坐标系中，若点E（a﹣1，a），F（b，a﹣b），线段EF的中点G恰好位于x轴上，且到y轴的距离是2，则2a+b的值等于　 　．
25．（4分）已知矩形ABCD中，BE平分∠ABC交矩形的一边于点E，若BD＝6，∠EBD＝15°，则线段AB的长为　 　．
五．解答题（共3小题，满分30分）
26．（8分）已知x＝﹣2，y＝+2．求：
（1）x2﹣y2；
（2）x2+2xy+y2．
27．（10分）某商店购进甲、乙两种商品，每件甲商品的进货价比每件乙商品的进货价高40元，已知15件甲商品的进货总价比26件乙商品的进货总价低60元．
（1）求甲、乙每件商品的进货价；
（2）若甲、乙两种商品共进货100件，要求两种商品的进货总价不高于8080元，同时甲商品按进价提高10%后的价格销售，乙商品按进价提高25%后的价格销售，两种商品全部售完后的销售总额不低于9250元，问共有几种进货方案？
（3）在条件（2）下，并且不再考虑其他因素，若甲乙两种商品全部售完，哪种方案利润最大？最大利润是多少？
28．（12分）如图，在平面直角坐标系xOy中，直线AB：y＝kx+3k（k≠0）交x轴于点B，交y轴于点A，AB＝3．
（1）求点A的坐标；
（2）点C为x轴正半轴上一点，∠BAO＝∠ACO，点M为线段AC上一动点，设M的纵坐标为a（a≠0），请用含a的代数式表示点M到y轴的距离d；
（3）在（2）的条件下，过点M作MN∥AB交x轴于点N，连接BM，AN，当△ABM为等腰三角形时，求△AMN的面积．












2021-2022学年成都市八年级上学期期末数学模拟试题
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）下列各数中，是无理数的是（　　）
A． B． C． D．3.1415
【答案】A
【解析】A、是无理数，故此选项正确；
B、＝2是整数，是有理数，故此选项错误；
C、是分数，是有理数，故此选项错误；
D、3.1415是有限小数，是有理数，故此选项错误．
故选：A．
2．（3分）下列各组线段不能构成直角三角形的是（　　）
A．2，3，4 B．3，4，5 C．1，1， D．6，8，10
【答案】A
【解析】A、∵22+32≠42，∴三角形不是直角三角形，故本选项正确；
B、∵32+42＝52，∴三角形是直角三角形，故本选项错误；
C、∵12+12＝（）2，∴三角形是直角三角形，故本选项错误；
D、∵62+82＝102，∴三角形不是直角三角形，故本选项错误．
故选：A．
3．（3分）﹣64的立方根是（　　）
A．﹣4 B．8 C．﹣4和4 D．﹣8和8
【答案】A
【解析】∵（﹣4）3＝﹣64
∴﹣64的立方根为﹣4，
故选：A．
4．（3分）若直线y＝kx+b经过第二、三、四象限，则直线y＝﹣bx+k不经过（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】B
【解析】∵直线y＝kx+b经过第二、三、四象限，
∴k＜0，b＜0，
∴﹣b＞0，
∴直线y＝﹣bx+k经过第一、三、四象限，不经过第二象限，
故选：B．
5．（3分）在直角坐标系xOy中，点A（a，3）与B（﹣1，b）关于y轴对称，则a，b的值分别为（　　）
A．a＝1，b＝3 B．a＝﹣1，b＝﹣3 C．a＝﹣1，b＝3 D．a＝1，b＝﹣3
【答案】A
【解析】∵点A（a，3）与B（﹣1，b）关于y轴对称，
∴a，b的值分别为1和3，
故选：A．
6．（3分）若是关于x，y的二元一次方程1﹣ay＝3x的一组解，则a的值为（　　）
A．﹣5 B．﹣1 C．2 D．7
【答案】A
【解析】根据题意，可得：1﹣a＝3×2，
∴1﹣6＝a，
解得a＝﹣5．
故选：A．
7．（3分）已知点P（2a+6，4+a）在第二象限，则a的取值范围是（　　）
A．﹣4＜a＜﹣3 B．a＜﹣3 C．a＞﹣3 D．a＞﹣4
【答案】A
【解析】∵点P（2a+6，4+a）在第二象限，
∴，
解得﹣4＜a＜﹣3，
故选：A．
8．（3分）下列命题是真命题的个数为（　　）
①两条直线被第三条直线所截，内错角相等．
②三角形的内角和是180°．
③在同一平面内，平行于同一条直线的两条直线平行．
④相等的角是对顶角．
⑤两点之间，线段最短．
A．2 B．3 C．4 D．5
【答案】B
【解析】①两条平行线被第三条直线所截，内错角相等，原命题是假命题．
②三角形的内角和是180°，是真命题．
③在同一平面内，平行于同一条直线的两条直线平行，是真命题．
④相等的角不一定是对顶角，原命题是假命题．
⑤两点之间，线段最短，是真命题；
故选：B．
9．（3分）一工坊用铁皮制作糖果盒，每张铁皮可制作盒身20个，或制作盒底30个，一个盒身与两个盒底配成一套糖果盒．现有35张铁皮，设用x张制作盒身，y张制作盒底，恰好配套制成糖果盒．则下列方程组中符合题意的是（　　）
A． B．
C． D．
【答案】C
【解析】设用x张制作盒身，y张制作盒底，恰好配套制成糖果盒，
根据题意可列方程组：，
故选：C．
10．（3分）直线y＝kx+b经过二、三、四象限，则直线y＝bx﹣k的图象只能是图中的（　　）
A． B．
C． D．
【答案】A
【解析】∵直线y＝kx+b经过二、三、四象限，
∴k＜0，b＜0，
∴直线y＝bx﹣k的图象经过第一、二、四象限，
故选：A．
二．填空题（共4小题，满分16分，每小题4分）
11．（4分）比较大小：2________4．
【答案】＜．
【解析】2＝，4＝，
∵28＜32，
∴＜，
∴2＜4．
12．（4分）若+|b+2|＝0，则a+b的值为________．
【答案】1．
【解析】∵+|b+2|＝0，
∴a﹣3＝0，b+2＝0，
解得：a＝3，b＝﹣2，
则a+b的值为：3﹣2＝1．
13．（4分）若一直角三角形两直角边长分别为6和8，则斜边长为________．
【答案】 10．
【解析】在直角三角形中，斜边的平方等于两条直角边平方和，
故斜边长＝＝10，
14．（4分）如图，在等边三角形ABC中，AD是高，点E为CD的中点，EF∥AC交AB于点F，交AD于点G，下列说法中正确的有________（填序号）
①∠AGF＝30°，
②AG＝GD，
③DB＝DG，
④EG＝2FG

【答案】①②④．
【解析】∵△ABC是等边三角形，AD⊥BC，
∴∠DAC＝30°．
∵EF∥AC，
∴∠AGF＝∠DAC＝30°，故①正确，
∵EG∥AC，DE＝EC，
∴AG＝DG，故②正确，
∵AD＝BD，
∴BD≠DG，故③错误，
设AC＝a，
∵∠DAC＝30°，
∴AD＝AC•cos30°＝a；
∵点G为AD的中点，
∴GE是△ADC的中位线，
∴点E时CD的中点，
∴EF＝AC＝a，
∵EF＝AC＝a，GE＝AC＝a，
∴EG＝2FG，故④正确．

三．解答题（共6小题，满分54分）
15．（10分）计算：
【答案】见解析
【解析】原式＝
＝
＝．
16．（12分）解方程组或不等式组：
（1）解方程组；
（2）解不等式组：并把解集在数轴上表示出来．
【答案】见解析
【解析】（1）方程组整理，得：，
①﹣②，得：2x＝﹣6，
解得x＝﹣3，
将x＝﹣3代入②，得：﹣6﹣3y＝1，
解得y＝﹣，
∴方程组的解为；
（2）解不等式+3≥x+1，得：x≤1，
解不等式1﹣3（x﹣1）＜8﹣x，得：x＞﹣2，
则不等式组的解集为﹣2＜x≤1，
将不等式组的解集表示在数轴上如下：

17．（6分）△ABC在直角坐标系中如图所示．
（1）在图中作出△ABC关于x轴的轴对称图形△A1B1C1；
（2）将△ABC先向上平移3个单位长度，再向左平移1个单位，画出平移后的△A2B2C2；
（3）求△ABC的面积．

【答案】见解析
【解析】（1）如图，△A1B1C1即为所求；

（2）如图，△A2B2C2即为所求；
（3）△ABC的面积为：3×3﹣1×2﹣1×3﹣2×3＝9﹣1﹣﹣3＝．
18．（8分）在前几天结束的2021年中考体育考试中，万中初三学子再传佳绩．万中体育组的殷老师随机抽取了甲、乙两班10名同学的体考成绩进行统计分析，整理如下：
甲班10同学的体考成绩：50，49，49，47，50，48，50，48，50，46．
甲乙两班抽取的学生成绩统计表：
班级
平均分
众数
中位数
甲
48.7
m
n
乙
48.3
49
48.5

根据以上信息，解答下列问题：
（1）填空：上述表格中，m＝________，n＝________
（2）根据以上数据，你认为甲、乙两班中哪个班的体考成绩更好？请说明理由（一条即可）．
（3）若万州中学初2021级约有1300人参加体考，请估计48分及以上的同学共有多少人？
【答案】见解析
【解析】（1）甲班10同学的体考成绩重新排列为：46，47，48，48，49，49，50，50，50，50，
所以其众数m＝50，中位数n＝＝49，
故答案为：50、49；
（2）甲班，
因为甲班学生的平均分48.7大于乙班学生的平均分48.3，说明其平均水平较好．
（3）1300×（名），
答：估计48分以上的共有975名．
19．（8分）如图，直线y＝﹣x+b与x轴，y轴分别交于点A，点B，与函数y＝kx的图象交于点M（1，2）．
（1）求k，b的值，并结合图象直接写出不等式0≤﹣x+b≤kx的解集；
（2）在x轴上有一点P，过点P作x轴的垂线，分别交函数y＝﹣+b和y＝kx的图象于点C，点D．若2CD＝OB，则点P的坐标为________．

【答案】见解析
【解析】（1）把M（1，2）代入y＝kx得k＝2；
把M（1，2）代入y＝﹣x+b得1＝﹣+b，解得b＝；
当y＝0时，﹣x+＝0，解得x＝5，则A（5，0），
所以不等式0≤﹣x+b≤kx的解集为1≤x≤5；
（2）当x＝0时，y＝﹣x+＝，则B（0，），
∴OB＝，
设P（m，0），则C（m，﹣m+），D（m，2m），
∵2CD＝OB，
∴2|﹣m+﹣2m|＝，
解得m＝或，
∴点P的坐标为（，0）或 （，0），
故答案为（，0）或 （，0）．

20．（10分）（1）如图1，等腰△ABC和等腰△ADE中，∠BAC＝∠DAE＝90°，B，E，D三点在同一直线上，求证：∠BDC＝90°；
（2）如图2，等腰△ABC中，AB＝AC，∠BAC＝90°，D是△ABC外一点，且∠BDC＝90°，求证：∠ADB＝45°；
（3）如图3，等边△ABC中，D是△ABC外一点，且∠BDC＝60°，
①∠ADB的度数；
②DA，DB，DC之间的关系．

【答案】见解析
【解析】（1）证明：如图1，设BD与AC交于点F，

∵∠BAC＝∠DAE＝90°，
∴∠BAE＝∠CAD，
在△ABE和△ACD中，

∴△ABE≌△ACD（SAS），
∴∠ABE＝∠ACD，
∵∠ABE+∠AFB＝90°，∠AFB＝∠CFD，
∴∠ACD+∠CFD＝90°，
∴∠BDC＝90°；
（2）如图2，过A作AE⊥AD交BD于E，

∵∠BAC＝∠DAE＝90°，
∴∠BAE＝∠CAD，
∵∠BAC＝∠BDC＝90°，∠AFB＝∠CFD，
∴∠ABE＝∠ACD，
在△ABE和△ACD中，
，
∴△ABE≌△ACD（ASA），
∴AE＝AD，
∴∠ADE＝∠AED＝45°；
（3）①如图3，在形内作∠DAE＝60°，AE交BD于E点，

与（2）同理△ABE≌△ACD，
∴AE＝DA，
∴△ADE是等边三角形，
∴∠ADE＝60°；
②∵BE＝DC，
∴DB＝BE+DE＝DA+DC．
四．填空题（共5小题，满分20分，每小题4分）
21．（4分）若y＝，则xy＝________．
【答案】2．
【解析】由题意得：，
解得：x＝2，
则y＝，
∴xy＝2．
22．（4分）一次函数y＝kx+4的图象上有一点P（2，n），将点P向右平移1个单位，再向下平移2个单位得到点Q，若点Q也在该函数的图象上，则n＝________．
【答案】0．
【解析】∵点P的坐标为（2，n），则点Q的坐标为（3，n﹣2），
依题意得：，
解得：n＝0，
23．（4分）关于x的不等式组有且只有4个整数解，则常数m的取值范围是________．
【答案】﹣2＜m≤﹣．
【解析】，
解不等式①得：x≥﹣1，
解不等式②得：x＜m+5，
∴原不等式组的解集为﹣1≤x＜m+5，
由不等式组的整数解只有4个，得到整数解为﹣1，0，1，2，
∴2＜m+5≤3，
∴﹣2＜m≤﹣
24．（4分）教材上曾让同学们探索过线段的中点坐标：在平面直角坐标系中，若两点A（x1，y1）、B（x2，y2），所连线段AB的中点是M，则M的坐标为（，），例如：点A（1，2）、点B（3，6），则线段AB的中点M的坐标为（，），即M（2，4）请利用以上结论解决问题：在平面直角坐标系中，若点E（a﹣1，a），F（b，a﹣b），线段EF的中点G恰好位于x轴上，且到y轴的距离是2，则2a+b的值等于________．
【答案】或﹣4．
【解析】∵点E（a﹣1，a），F（b，a﹣b），
∴中点G（，），
∵中点G恰好位于x轴上，且到y轴的距离是2，
∴，
解得：，，
∴2a+b＝或﹣4；
25．（4分）已知矩形ABCD中，BE平分∠ABC交矩形的一边于点E，若BD＝6，∠EBD＝15°，则线段AB的长为________．
【答案】3或．
【解析】有两种情况：
∵四边形ABCD是矩形，
∴∠A＝∠ABC＝∠C＝90°，
∵BE平分∠ABC，
∴∠ABE＝∠CBE＝45°，
①当E在AD上时，如图1，
∵∠EBD＝15°，
∴∠DBC＝45°﹣15°＝30°，
∴CD＝BD＝3，
即AB＝CD＝3；
②当E在CD上时，如图2，
∵∠EBD＝15°，
∴∠ABD＝45°﹣15°＝30°，
∴AD＝BD＝3，
在Rt△ABD中，由勾股定理得：AB＝＝3．

五．解答题（共3小题，满分30分）
26．（8分）已知x＝﹣2，y＝+2．求：
（1）x2﹣y2；
（2）x2+2xy+y2．
【答案】见解析
【解析】（1）当x＝﹣2，y＝+2时，
原式＝（x+y）（x﹣y）
＝（）（）
＝2×（﹣4）
＝﹣8；
（2）当x＝﹣2，y＝+2时，
原式＝（x+y）2
＝（）2
＝（2）2
＝20．
27．（10分）某商店购进甲、乙两种商品，每件甲商品的进货价比每件乙商品的进货价高40元，已知15件甲商品的进货总价比26件乙商品的进货总价低60元．
（1）求甲、乙每件商品的进货价；
（2）若甲、乙两种商品共进货100件，要求两种商品的进货总价不高于8080元，同时甲商品按进价提高10%后的价格销售，乙商品按进价提高25%后的价格销售，两种商品全部售完后的销售总额不低于9250元，问共有几种进货方案？
（3）在条件（2）下，并且不再考虑其他因素，若甲乙两种商品全部售完，哪种方案利润最大？最大利润是多少？
【答案】见解析
【解析】（1）设每件甲商品的进货价为x元，每件乙商品的进货价为y元，
依题意，得：，
解得：．
答：每件甲商品的进货价为100元，每件乙商品的进货价为60元．
（2）设购进m件甲商品，则购进（100﹣m）件乙商品，
依题意，得：，
解得：50≤m≤52，
又∵m为正整数，
∴m可以取50，51，52，
∴共有3种进货方案，方案1：购进50件甲商品，50件乙商品；方案2：购进51件甲商品，49件乙商品；方案3：购进52件甲商品，48件乙商品．
（3）设获得的总利润为w元，则w＝100×10%m+60×25%（100﹣m）＝﹣5m+1500，
∵﹣5＜0，
∴w随m值的增大而减小，
∴当m＝50时，w取得最大值，最大值＝﹣5×50+1500＝1250．
答：方案1购进50件甲商品，50件乙商品利润最大，最大利润是1250元．
28．（12分）如图，在平面直角坐标系xOy中，直线AB：y＝kx+3k（k≠0）交x轴于点B，交y轴于点A，AB＝3．
（1）求点A的坐标；
（2）点C为x轴正半轴上一点，∠BAO＝∠ACO，点M为线段AC上一动点，设M的纵坐标为a（a≠0），请用含a的代数式表示点M到y轴的距离d；
（3）在（2）的条件下，过点M作MN∥AB交x轴于点N，连接BM，AN，当△ABM为等腰三角形时，求△AMN的面积．

【答案】见解析
【解析】（1）由题意，直线直线AB：y＝kx+3k（k≠0）交x轴于点B（﹣3，0），交y轴于点A（0，3k），
在Rt△AOB中，AB2＝OA2+OB2，
∴32+（3k）2＝（3）2，
∴k＝3或﹣3（舍弃），
∴AO＝9，
∴A（0，9）．

（2）如图1中，过点C作∠ACB的角平分线交AB于H．

∴∠BCH＝∠ACB，
∵∠BAO＝∠ACO，
∴∠BCH＝∠BAO，
∵∠BAO+∠ABC＝90°，
∴∠BCH+∠ABO＝90°，
∴∠CHB＝∠CHA＝90°，
∵CH＝CH，∠HCB＝∠HCA，
∴△ACH≌△BCH（ASA），
∴CA＝CB，
设C（m，0），则BC＝m+3，AC＝，
∴m+3＝，
∴m＝12，
∴C（12，0），
∴直线AC的解析式为y＝﹣x+9，
∵M的纵坐标为a（a≠0），点M横坐标为d，
∴a＝﹣d+9，
∴d＝﹣a+12．

（3）在（2）的条件下，AC＝BC，
∵MN∥AB，
∴AM＝BN，S△AMN＝S△BMN，
①当AB＝BM时，过点B作BG⊥AC于G，

∴AG＝MG，
∵∠AOB＝∠BGA，∠ABC＝∠BAC，AB＝BA，
∴△ABO≌△BAG（AAS），
∴BO＝AG＝3，
∴BN＝AM＝2AG＝6，
∴N（3，0），
∵MN∥AB，
∵直线MN：y＝3x+b过点N（3，0），
∴b＝﹣9，
∴直线MN的表达式为y＝3x﹣9，
由，解得，
∴M（，），
∴S△AMN＝S△BMN＝•BN•yM＝×6×＝．
②当AB＝AM时，N（﹣3+3，0）
∴直线MN的表达式为y＝3x+9﹣9，

由，解得，
∴M（，），
∴S△AMN＝S△BMN＝•BN•yM＝3×＝