2020-2021学年人教版数学八年级下册期末综合检测试卷（word版 含答案）

这是一份2020-2021学年人教版数学八年级下册期末综合检测试卷（word版 含答案），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

期末达标检测试卷
(时间：120分钟　满分：100分)
一、选择题(本大题共8个小题，每小题只有一个正确选项，每小题3分，共24分)
1．已知x＝＋1，y＝－1，则x2＋xy＋y2的值为(　　)
A．10 B．8
C．6 D．4
2．已知x，y为正数，且|x2－4|＋(y2－3)2＝0.如果以x，y为直角边的长作一个直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为(　　)
A．5 B．25
C．7 D．15
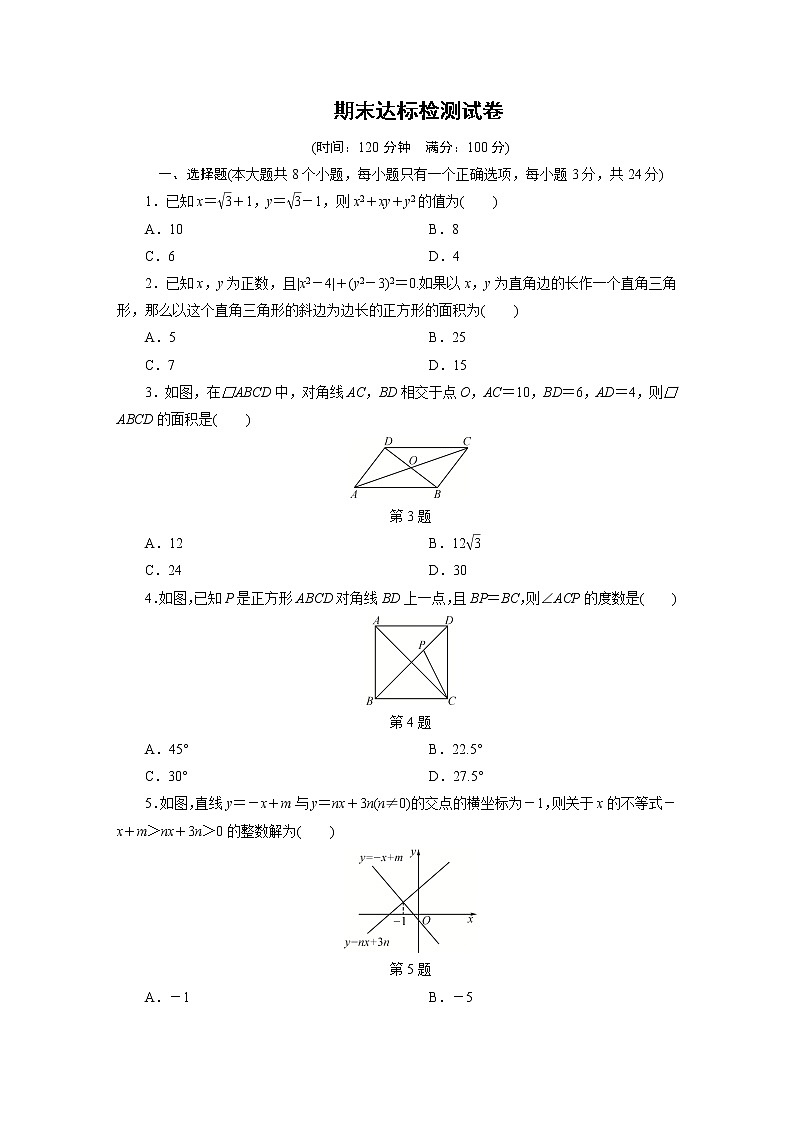
3．如图，在□ABCD中，对角线AC，BD相交于点O，AC＝10，BD＝6，AD＝4，则□ABCD的面积是(　　)

第3题
A．12 B．12
C．24 D．30
4．如图，已知P是正方形ABCD对角线BD上一点，且BP＝BC，则∠ACP的度数是(　　)

第4题
A．45° B．22.5°
C．30° D．27.5°
5．如图，直线y＝－x＋m与y＝nx＋3n(n≠0)的交点的横坐标为－1，则关于x的不等式－x＋m＞nx＋3n＞0的整数解为(　　)

第5题
A．－1 B．－5
C．－4 D．－2
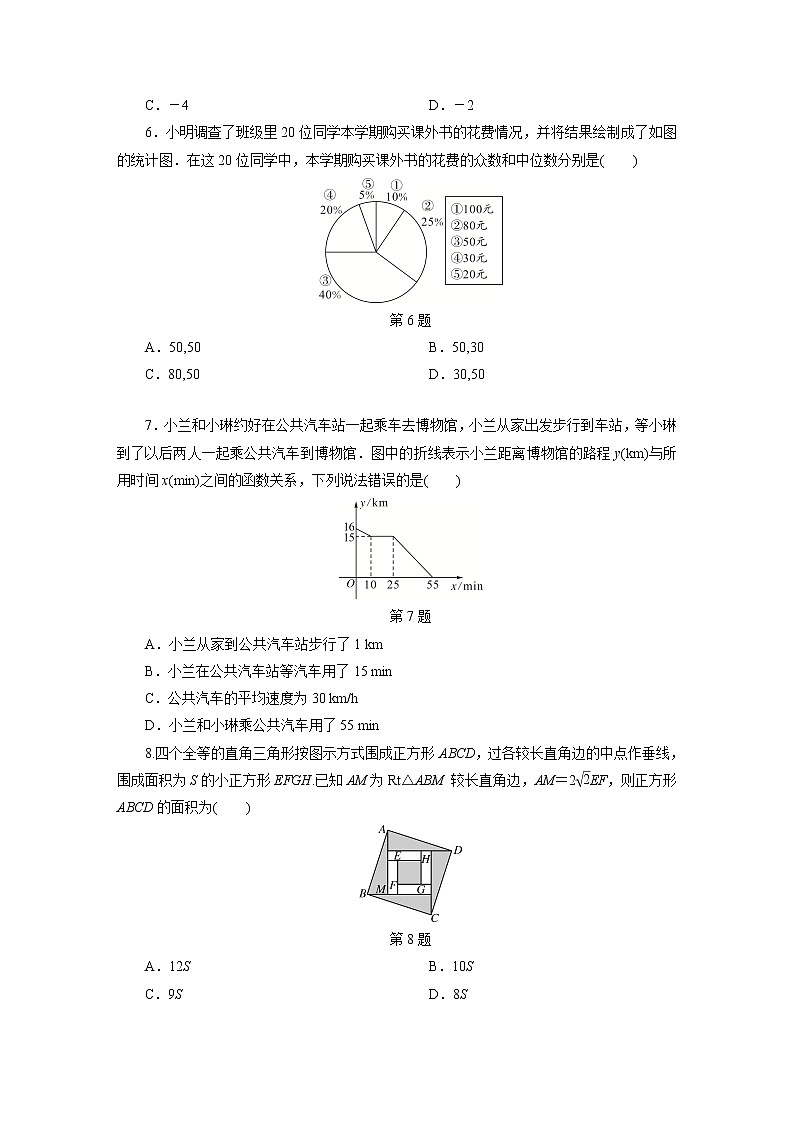
6．小明调查了班级里20位同学本学期购买课外书的花费情况，并将结果绘制成了如图的统计图．在这20位同学中，本学期购买课外书的花费的众数和中位数分别是(　　)

第6题
A．50,50 B．50,30
C．80,50 D．30,50
　
7．小兰和小琳约好在公共汽车站一起乘车去博物馆，小兰从家出发步行到车站，等小琳到了以后两人一起乘公共汽车到博物馆．图中的折线表示小兰距离博物馆的路程y(km)与所用时间x(min)之间的函数关系，下列说法错误的是(　　)

第7题
A．小兰从家到公共汽车站步行了1 km
B．小兰在公共汽车站等汽车用了15 min
C．公共汽车的平均速度为30 km/h
D．小兰和小琳乘公共汽车用了55 min
8.四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH.已知AM为Rt△ABM 较长直角边，AM＝2EF，则正方形ABCD的面积为(　　)

第8题
A．12S B．10S
C．9S D．8S
二、填空题(本大题共6个小题，每小题3分，共18分)
9．函数y＝的自变量x的取值范围是________．
10．已知一次函数y＝kx＋6的图象经过点A(2，－2)，则k的值为________．
11．一组数据3,4,6,8，x的中位数是x，且x是满足不等式组的整数，则这组数据的平均数是________．
12．一食堂需要购买盒子存放食物，盒子有A，B两种型号，单个盒子的容量和价格如表．现有15升食物需要存放且要求每个盒子要装满，由于A型号盒子正做促销活动：购买三个及三个以上可一次性返还现金4元，则一次性购买盒子所需要的最少费用为________元.
型　号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
13.【云南大理期末】如图，在□ABCD中，点E，F分别在边BC，AD上，请添加一个条件________使四边形AECF是平行四边形(只填一个即可)．

第13题
14．如图，分别以Rt△ABC的斜边AB、直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB＝90°，∠BAC＝30°.下列结论：①EF⊥AC；②四边形ADFE为菱形；③AD＝4AG；④FH＝BD．其中正确的结论为________．(请将所有正确结论的序号都填上)

第14题
选择、填空题答题卡
一、选择题(每小题3分，共24分)
题号
1
2
3
4
得分
答案




题号
5
6
7
8

答案





二、填空题(每小题3分，共18分)　　得分：________
9．________　 　　10.________　　　11.________
12．________　　　13.________　　　14.________
三、解答题(本大题共9个小题，共58分)
15．(本小题6分)计算：
(1)(－)×＋|－2|－－1；


(2)(7＋4)(7－4)－(3－1)2.



16．【云南玉溪期末】(本小题4分)如图，P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时针旋转90°，得到线段CQ，连接BP，DQ.求证：∠CBP＝∠CDQ.


第16题






17．(本小题4分)如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作BC的平行线交CE的延长线于点F，连接BF.求证：四边形AFBD是平行四边形．

第17题



18．(本小题6分)某市江边的景观区内有一块四边形空地，如图所示．景区管理人员想在这块空地上铺满观赏草坪，需要测量其面积，经技术人员测量，∠ABC＝90°，AB＝20米，BC＝15米，CD＝7米，AD＝24米．
(1)请你帮助管理人员计算出这个四边形对角线AC的长度；
(2)请你用学过的知识帮助管理员计算出这块空地的面积．

第18题



19．(本小题6分)如图，直线l1的解析式为y＝2x－2，且直线l1与x轴交于点D，直线l2与y轴交于点A，且经过点B(3,1)，直线l1，l2交于点C(2，m)．
(1)求直线l2的解析式；
(2)根据图象，求四边形OACD的面积．

第19题







20．(本小题7分)某校计划组织全校1300名师生到林业部门规划的林区植树，经研究，决定租用当地租车公司提供的A，B两种型号客车共50辆作为交通工具．下表是租车公司提供给学校有关两种型号客车的载客量与租金信息.
型号
载客量
租金单价
A
30人/辆
300元/辆
B
20人/辆
240元/辆
注：载客量指的是每辆客车最多可载该校师生的人数．
(1)设租用A型号客车x辆，租车总费用为y元，求y与x的函数解析式，并直接写出x的取值范围；
(2)若要使租车总费用不超过13 980元，一共有几种租车方案？哪种租车方案最省钱？








21．(本小题7分)某中学举行“中国梦——校园好声音”歌手大赛，初、高中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
(1)根据图示将表格补充完整；

平均数/分
中位数/分
众数/分
初中部

85

高中部
85

100
(2)结合两队决赛成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
(3)计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．

第21题



22．(本小题8分)如图，在平面直角坐标系中，直线y＝－x＋b分别与x轴、y轴交于点A、B，且点A的坐标为(8,0)，四边形ABCD是正方形．
(1)b＝________；
(2)求点D的坐标；
(3)M是线段AB上的一个动点(点A，B除外)，试探索在x轴上方是否存在另一个点N，使得以O，B，M，N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．

第22题




23．(本小题10分)已知四边形ABCD是正方形，点P在直线BC上，点G在直线AD上(点P，G都不与正方形的顶点重合，且在CD的同侧)，PD＝PG，DF⊥PG于点H，交直线AB于点F.将线段PG绕点P逆时针旋转90°得到线段PE，连接EF.
(1)如图1，当点P与点G分别在线段BC与线段AD上时，
①求证：DG＝2PC；
②求证：四边形PEFD是菱形；
(2)如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．

第23题



参考答案

一、1.A　2.C　3.C　4.B　5.D　6.A　7.D　8.C
二、9.x>0　10.－4　11.5　12.29　13.AE∥CF(答案不唯一)
14．①③④　解析：∵△ACE是等边三角形，∴∠EAC＝60°，AE＝AC.∵∠BAC＝30°，∴∠FAE＝∠ACB＝90°，AB＝2BC.∵F为AB的中点，∴AB＝2AF，∴BC＝AF，∴△ABC≌△EFA(SAS)，∴FE＝AB，∠AEF＝∠BAC＝30°， ∠EHA＝180°－∠AEF－∠EAC＝90°，∴EF⊥AC，故①正确；∵EF⊥AC，∠ACB＝90°，∴HF∥BC.∵F是AB的中点，∴HF＝BC.∵BC＝AB，AB＝BD，∴HF＝BD，故④正确；∵AD＝BD，BF＝AF，∴∠DFB＝90°，∠BDF＝30°.∵∠FAE＝90°，∴∠DFB＝∠EAF.∵∠AEF＝30°，∴∠BDF＝∠AEF，∴△DBF≌△EFA(AAS)，∴AE＝DF.∵FE＝BD＝AD，∴四边形ADFE为平行四边形，∴AG＝AF，∴AG＝AB.又∵AE≠EF，AD＝AB，∴四边形ADFE不是菱形，AD＝4AG，故②不正确，③正确．综上，①③④正确．
三、15.解：(1)原式＝－＋2－－2＝－2－＝－3.　(2)原式＝72－(4)2－(45－2×3＋1)＝1－45＋6－1＝6－45.
16．证明：由题意，得∠PCQ＝90°，PC＝QC.∵四边形ABCD是正方形，∴BC＝DC，∠BCD＝90°，∴∠BCD－∠PCD＝∠PCQ－∠PCD，即∠BCP＝∠DCQ.在△BCP和△DCQ中，∵△BCP≌△DCQ(SAS)，∴∠CBP＝∠CDQ.
17．证明：∵E是AD的中点，∴AE＝DE.又∵AF∥BD，∴∠FAE＝∠CDE.又∵∠FEA＝∠CED，∴△AFE≌△DCE(ASA)，∴AF＝CD.又∵D是BC的中点，∴BD＝CD，∴AF＝BD.∵AF∥BD，∴四边形AFBD是平行四边形．
18．解：(1)连接AC.在Rt△ABC中，∵∠ABC＝90°，AB＝20，BC＝15，∴AC＝＝＝25(米)．故四边形对角线AC的长度为25米．　(2)在△ADC中，∵CD＝7，AD＝24，AC＝25，∴AD2＋CD2＝242＋72＝625＝252＝AC2，∴△ADC为直角三角形，且∠ADC＝90°，∴S四边形ABCD＝S△ABC＋S△ADC＝×15×20＋×7×24＝234(平方米)，∴这块空地的面积为234平方米．
19．解：(1)∵点D是直线l1：y＝2x－2与x轴的交点，∴令y＝0，即0＝2x－2，解得x＝1，∴D(1,0)．将点C(2，m)代入直线l1：y＝2x－2，得m＝2×2－2＝2，∴C(2,2)．设直线l2的解析式为y＝kx＋b.∵点C(2,2)、B(3,1)在直线l2上，∴解得∴直线l2的解析式为y＝－x＋4.　(2)过点C作x轴的平行线交y轴于点G.∵点A是直线l2与y轴的交点，∴令x＝0，∴y＝4，∴A(0,4)．∵C(2,2)，∴AG＝2，CG＝2，GO＝2，∴S四边形OACD＝S梯形ODCG＋S△AGC＝×(1＋2)×2＋×2×2＝5.
20．解：(1)根据题意，得y＝300x＋240(50－x)＝60x＋12 000.∵30x＋20(50－x)≥1300，∴x≥30，∴y与x的函数解析式为y＝60x＋12 000(x≥30，x为整数)．　(2)根据题意，得60x＋12 000≤13 980，解得x≤33.又∵x≥30，∴30≤x≤33，即共有4种租车方案．方案1：租A型号客车30辆，B型号客车20辆；方案2：租A型号客车31辆，B型号客车19辆；方案3：租A型号客车32辆，B型号客车18辆；方案4：租A型号客车33辆，B型号客车17辆．∵60＞0，∴y随x的增大而增大，∴租车方案1最省钱．
21．(1)85　85　80　(2)解：∵两队成绩的平均数相同，初中代表队的中位数较大，∴在平均数相同的情况下，中位数较大的初中代表队的决赛成绩较好．　(3)解：s＝[(75－85)2＋(80－85)2＋(85－85)2＋(85－85)2＋(100－85)2]＝70，s＝[(70－85)2＋(100－85)2＋(100－85)2＋(75－85)2＋(80－85)2]＝160.∵s＜s，∴初中代表队选手成绩较为稳定．
22．(1)6　(2)解：如图1，过点D作DE⊥x轴于点E，则∠AOB＝∠DEA＝90°.∵四边形ABCD是正方形，∴AB＝DA，∠BAD＝90°，∴∠1＋∠2＝90°.∵∠2＋∠3＝90°，∴∠1＝∠3.在△AOB和△DEA中，∵∴△AOB≌△DEA(AAS)，∴OA＝DE＝8，OB＝AE＝6，∴OE＝OA＋AE＝8＋6＝14，∴点D的坐标为(14,8)．　(3)解：存在．①如图2，当OM＝MB＝BN＝NO时，四边形OMBN为菱形．连接NM，交OB于点P，则NM与OB互相垂直平分，∴OP＝OB＝3.当y＝3时，－x＋6＝3，解得x＝4.∴点M的坐标为(4,3)，∴点N的坐标为(－4,3)．②如图3，当OB＝BN＝NM＝MO＝6时，四边形BOMN为菱形．延长NM交x轴于点P，则MP⊥x轴．∵点M在直线y＝－x＋6上，∴设点M的坐标为(0
图1

图2


图3

23．(1)证明：①过点P作PM⊥DG于点M.∵PD＝PG，∴MG＝MD.∵四边形ABCD为正方形，∴四边形PCDM为矩形，∴PC＝MD，∴DG＝2PC.　②∵四边形ABCD为正方形，∴AD＝AB.∵四边形ABPM为矩形，∴AB＝PM，∴AD＝PM.∵DF⊥PG，∴∠DHG＝90°，∴∠GDH＋∠DGH＝90°.∵∠MGP＋∠MPG＝90°，∴∠GDH＝∠MPG.在△ADF和△MPG中，∵∴△ADF≌△MPG(ASA)，∴DF＝PG.∵PD＝PG，∴DF＝PD.∵线段PG绕点P逆时针旋转90°得到线段PE，∴∠EPG＝90°，PE＝PG，∴PE＝PD＝DF.∵DF⊥PG，∴DF∥PE，∴四边形PEFD为平行四边形．又∵DF＝PD，∴四边形PEFD为菱形．　(2)解：四边形PEFD是菱形．证明：过点P作PM⊥DG于点M.易得△ADF≌△MPG，∴DF＝PG.∵PD＝PG，∴DF＝PD.∵线段PG绕点P逆时针旋转90°得到线段PE，∴∠EPG＝90°，PE＝PG，∴PE＝PD＝DF.又∵DF⊥PG，∴DF∥PE.又∵DF＝PE，∴四边形PEFD为平行四边形．∵DF＝PD，∴四边形PEFD为菱形．