期末复习试卷（一）2021-2022学年苏科版九年级数学上册（word版 含答案）

苏科版2021—2022学年秋季九年级数学期末复习试卷（一）

一．选择题（共10小题，每小题3分，共30分）

1．抛物线与轴的交点坐标为　　

A． B． C． D．

2．如图，在平面直角坐标系中，的顶点，分别在轴、轴上，，，斜边轴．若反比例函数的图象经过的中点，则的值

为　　

A．4 B．5 C．6 D．8

3．如图，、、、是上的四个点，，且平分，则的形状是　　

A．直角三角形 B．等腰三角形 

C．等边三角形 D．等腰直角三角形

4．如图，圆锥的底面半径为6，母线长为10，则圆锥的侧面积是　　

A． B． C． D．

5．如图，在边长为1的小正方形网格中，的三个顶点均在格点上，则的值

为　　

A． B． C． D．

6．如图，一张矩形纸片的长，宽，把这张纸片沿一组对边和的中点连线对折，对折后所得矩形与原矩形相似，则的值

为　　

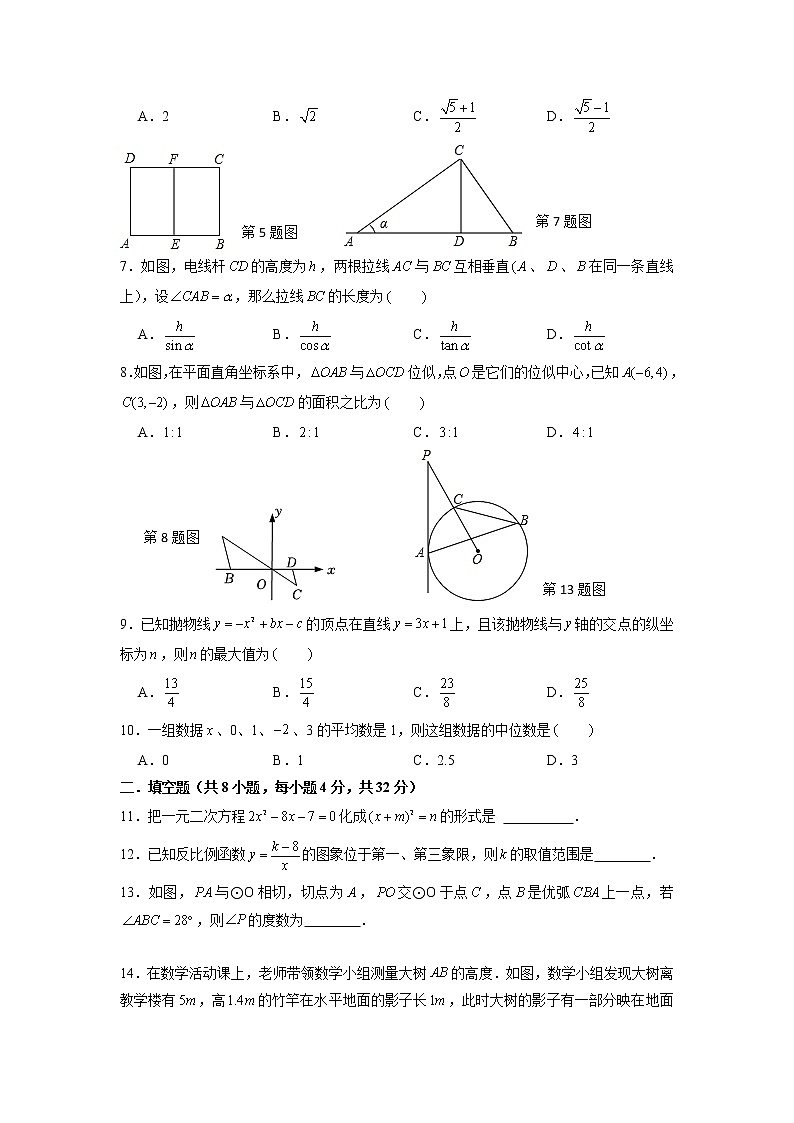
A．2 B． C． D．

7．如图，电线杆的高度为，两根拉线与互相垂直、、在同一条直线上），设，那么拉线的长度为　　

A． B． C． D．

8．如图，在平面直角坐标系中，与位似，点是它们的位似中心，已知，，则与的面积之比为　　

A． B． C． D．

9．已知抛物线的顶点在直线上，且该抛物线与轴的交点的纵坐标为，则的最大值为　　

A． B． C． D．

10．一组数据、0、1、、3的平均数是1，则这组数据的中位数是　　

A．0 B．1 C．2.5 D．3

二．填空题（共8小题，每小题4分，共32分）

11．把一元二次方程化成的形式是 　      　．

12．已知反比例函数的图象位于第一、第三象限，则的取值范围是　    　．

13．如图，与⊙O相切，切点为，交⊙O于点，点是优弧上一点，若，则的度数为　    　．

14．在数学活动课上，老师带领数学小组测量大树的高度．如图，数学小组发现大树离教学楼有，高的竹竿在水平地面的影子长，此时大树的影子有一部分映在地面上，还有一部分映在教学楼的墙上，墙上的影子高为，那么这棵大树高 　    　．

15．为了在校运会中取得更好的成绩，小丁积极训练，在某次试投中铅球所经过的路线是如图所示的抛物线的一部分．已知铅球出手处距离地面的高度是1.68米，当铅球运行的水平距离为2米时，达到最大高度2米的处，则小丁此次投掷的成绩是 　    　米．

16．如图，等边内接于⊙O，为⊙O内接正十二边形的一边，，则图中阴影部分的面积等于　    　．

17．如图，在中，点是上一点，若，且，，则线段的长度为　    　．

18．如图已知，，，是轴上的点，且，分别过点，，，作轴的垂线交二次函数的图象于点，，，，若记△的面积为，过点作于点，记△的面积为，过点作于点，记△的面积为，依次进行下去，则　   　，最后记△的面积为，则　    　．

三．解答题（共9小题，满分78分，其中19题6分，20--24每小题8分，25、26每小题10分，27题12分）

19．计算：．

20．先化简，再求值：，其中满足方程．

21．一个不透明的袋子中装有9个红球和2个白球；这些球除颜色外都相同从中任意摸出一个球．

（1）“摸到红球”是 　  　事件，“摸到黑球”是 　  　事件．（填“不可能”或“必然”或“随机”

（2）如果要使摸到白球的概率为，需要往盒子里再放入多少个白球？

22．如图，为⊙O的直径，，为圆上的两点，，弦，相交于点．

（1）求证： ；

（2）若，，求⊙O的半径．

23．返校复学之际，育才学校为每个班级准备了免洗抑菌洗手液．去市场购买时发现当购买量不超过100瓶时，免洗抑菌洗手液的单价为8元；超过100瓶时，每增加10瓶，每瓶单价就降低0.2元，但最低价格不能低于每瓶5元，设学校共买了瓶免洗抑菌洗手液．

（1）当时，每瓶洗手液的价格是 　  　元；当时，每瓶洗手液的价格

是 　   　元；当时，每瓶洗手液的价格为 　    　元（用含的式子表示）；

（2）若学校一次性购买洗手液共花费1200元，问一共购买了多少瓶洗手液？

24．如图1，是一款手机支架图片，由底座、支撑板和托板构成．图2是其侧面结构示意图，量得托板长，支撑板长，底座长，托板联结在支撑板顶端点处，且，托板可绕点转动，支撑板可绕点转动．如图2，若，，求点到直线的距离（精确到．（参考数值，，，

25．如图，预防新冠肺炎疫情期间，某校在校门口用塑料膜围成一个临时隔离区，隔离区一面靠长为的墙，隔离区分成两个区域，中间用塑料膜隔开．已知整个隔离区塑料膜总长为，如果隔离区出入口的大小不计，并且隔离区靠墙的面不能超过墙长，设垂直于墙的一边为，隔离区面积为．

（1）求关于的函数解析式，并写出的取值范围；

（2）求隔离区面积的最大值．

26．如图，在矩形中，是上的一点，沿将对折，点刚好落在边的点上．

（1）求证：．

（2）若，，求．

27．如图，平面直角坐标系中，是坐标原点，抛物线与轴交于、两点（点在点的左侧），点坐标是．抛物线与轴交于点，点是抛物线的顶点，连接．

（1）求抛物线的函数表达式并直接写出顶点的坐标．

（2）直线与抛物线对称轴交于点，点为直线上一动点．

①当的面积等于面积的2倍时，求点的坐标；

②在①的条件下，当点在轴上方时，过点作直线垂直于，直线交直线于点，点在直线上，且时，请直接写出的长．

苏科版2021—2022学年秋季九年级数学期末复习试卷（一）参考简答

一．选择题（共10小题）

1．．  2．．  3．．  4．．  5．．  6．．  7．．  8．．

9．．  10．．

二．填空题（共8小题）

11．　．　．  12．　　．  13．　　．  14． 　9　．

15． 　7　．  16．　　．  17．　2　．  18．　　，　　．

三．解答题（共9小题）

19．计算：．

【解】：原式

；

20．先化简，再求值：，其中满足方程．

【解】：原式

，

方程，

分解因式得：，

解得：或，

当时，原分式没有意义；

当时，原式．

21．一个不透明的袋子中装有9个红球和2个白球；这些球除颜色外都相同从中任意摸出一个球．

（1）“摸到红球”是 　  　事件，“摸到黑球”是 　  　事件．（填“不可能”或“必然”或“随机”

（2）如果要使摸到白球的概率为，需要往盒子里再放入多少个白球？

【解】：（1）不透明的袋子中装有9个红球和2个白球，

“摸到红球”是随机事件，“摸到黑球”是不可能事件．

（2）设需要往盒子里再放入个白球，根据题意得： ，

解得：，

经检验是原方程的解，

则需要往盒子里再放入4个白球．

22．如图，为的直径，，为圆上的两点，，弦，相交于点．

（1）求证：；

（2）若，，求的半径．

【解】：（1）证明是的直径，

，

，

．

，

；

（2）由（1）可知，

又，

．

设的半径为，

，

，

由勾股定理得：，

，

的半径为10．

23．返校复学之际，育才学校为每个班级准备了免洗抑菌洗手液．去市场购买时发现当购买量不超过100瓶时，免洗抑菌洗手液的单价为8元；超过100瓶时，每增加10瓶，每瓶单价就降低0.2元，但最低价格不能低于每瓶5元，设学校共买了瓶免洗抑菌洗手液．

（1）当时，每瓶洗手液的价格是 　  　元；当时，每瓶洗手液的价格

是 　   　元；当时，每瓶洗手液的价格为 　   　元（用含的式子表示）；

（2）若学校一次性购买洗手液共花费1200元，问一共购买了多少瓶洗手液？

【解】：（1）当时，每瓶洗手液的价格是8元；当时，每瓶洗手液的价格是（元；当时，每瓶洗手液的价格为（元，当时，每瓶洗手液的价格是5元．

（2）（元（元，

．

当时，，

整理得：，

解得：，（不合题意，舍去）；

当时，，

解得：（不合题意，舍去）．

答：一共购买了200瓶洗手液．

24．如图1，是一款手机支架图片，由底座、支撑板和托板构成．图2是其侧面结构示意图，量得托板长，支撑板长，底座长，托板联结在支撑板顶端点处，且，托板可绕点转动，支撑板可绕点转动．如图2，若，，求点到直线的距离（精确到．（参考数值，，，

【解】：如图2，过作，垂足为，过点作，垂足为，过点作，垂足为，则四边形为矩形，

，

在中，，

，

在中，，，

，

，

．

答：点到直线的距离约为．

25．如图，预防新冠肺炎疫情期间，某校在校门口用塑料膜围成一个临时隔离区，隔离区一面靠长为的墙，隔离区分成两个区域，中间用塑料膜隔开．已知整个隔离区塑料膜总长为，如果隔离区出入口的大小不计，并且隔离区靠墙的面不能超过墙长，设垂直于墙的一边为，隔离区面积为．

（1）求关于的函数解析式，并写出的取值范围；

（2）求隔离区面积的最大值．

【解】：（1）垂直于墙的一边为，则隔离区的另一边为，

，化简得，

根据题意，得不等式组，

解得：，

关于的函数解析式，的取值范围：；

（2），

该抛物线开口向下，对称轴为直线，

当时，随的增大而减小，

当时，的值最大，最大值，

答：隔离区面积最大值为．

26．如图，在矩形中，是上的一点，沿将对折，点刚好落在边的点上．

（1）求证：．

（2）若，，求．

【解】：（1）证明：在矩形中，沿将对折，点刚好落在边的点上，

，

，

，

，

，

，

又，

．

（2）四边形为矩形，，，

，，

，

，

在中，由勾股定理得：，

，

，

，

，

，

，

在中，．

27．如图，平面直角坐标系中，是坐标原点，抛物线与轴交于、两点（点在点的左侧），点坐标是．抛物线与轴交于点，点是抛物线的顶点，连接．

（1）求抛物线的函数表达式并直接写出顶点的坐标．

（2）直线与抛物线对称轴交于点，点为直线上一动点．

①当的面积等于面积的2倍时，求点的坐标；

②在①的条件下，当点在轴上方时，过点作直线垂直于，直线交直线于点，点在直线上，且时，请直接写出的长．

【解】：（1）由题意得，，

，

，

．

（2）①如图1，

作于，

，，

直线，

，可设，

，

是等腰直角三角形，

，

，

，

或．

或．

②如图2，

设，

由得，

，

化简，得

，

，，

，，，

作于，

，

，

，

即：，

，

，，

设直线是：， ，

，，

，

由得，

，

，

，

．