2021-2022学年冀教版九年级上学期数学期末练习试卷（word版 含答案）

这是一份2021-2022学年冀教版九年级上学期数学期末练习试卷（word版 含答案），共21页。试卷主要包含了方程x2＝4x的根是，若反比例函数y＝，如图，几何体的左视图是，若点A等内容，欢迎下载使用。

2021-2022学年冀教新版九年级上学期数学期末练习试卷
一．选择题（共16小题，满分42分）
1．方程x2＝4x的根是（　　）
A．x＝4 B．x＝0 C．x1＝0，x2＝4 D．x1＝0，x2＝﹣4
2．在演讲比赛活动中，7位评委分别给出某位选手的原始评分，评定该选手成绩时，从7个原始评分中去掉一个最高分和一个最低分，得到5个有效评分．5个有效评分与7个原始评分相比，这两组数据不可能变化的是（　　）
A．中位数 B．众数 C．平均数 D．方差
3．若反比例函数y＝（m+3）的图象在第一、三象限，则m的值为（　　）
A．1或﹣3 B．3或﹣1 C．﹣3 D．1
4．二次函数y＝kx2﹣6x+3的图象与x轴有交点，则k的取值范围是（　　）
A．k＜3 B．k＜3且k≠0 C．k≤3 D．k≤3且k≠0
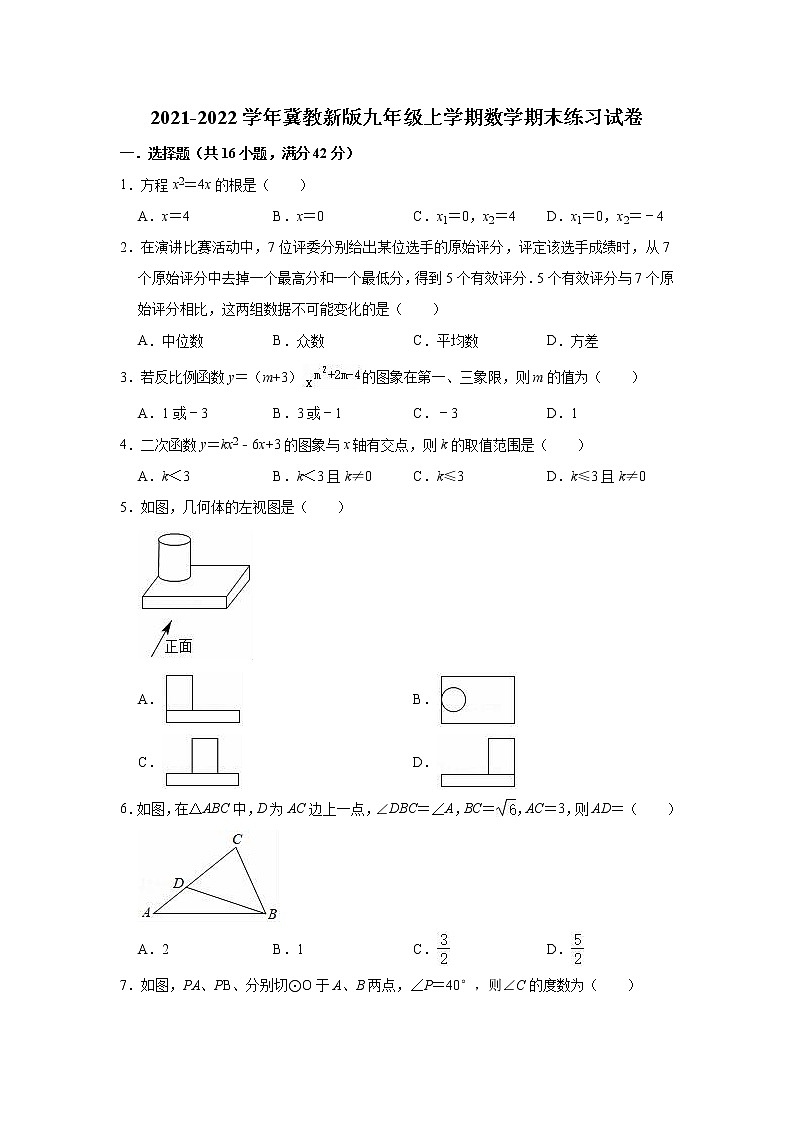
5．如图，几何体的左视图是（　　）

A． B．
C． D．
6．如图，在△ABC中，D为AC边上一点，∠DBC＝∠A，BC＝，AC＝3，则AD＝（　　）

A．2 B．1 C． D．
7．如图，PA、PB、分别切⊙O于A、B两点，∠P＝40°，则∠C的度数为（　　）

A．40° B．140° C．70° D．80°
8．一个圆锥的底面半径是4cm，其侧面展开图的圆心角是120°，则圆锥的母线长是（　　）
A．8cm B．12cm C．16cm D．24cm
9．若点A（﹣2020，y1）、B（2021，y2）都在双曲线上，且y1＞y2，则a的取值范围是（　　）
A．a＜0 B．a＞0 C． D．
10．已知抛物线y＝x2+bx+4的顶点在x轴上，则b的值为（　　）
A．2 B．4 C．﹣4 D．±4
11．在同一平面直角坐标系中反比例函数y＝与一次函数y＝x+a（a≠0）的图象大致是（　　）
A． B．
C． D．
12．如图，在△ABC与△ADE中，∠ACB＝∠AED＝90°，∠ABC＝∠ADE，连接BD、CE，若AC：BC＝3：4，则BD：CE为（　　）

A．5：3 B．4：3 C．：2 D．2：
13．如图，正方形ABCD和正△AEF都内接于⊙O，EF与BC、CD分别相交于点G、H，则的值是（　　）

A． B． C． D．2
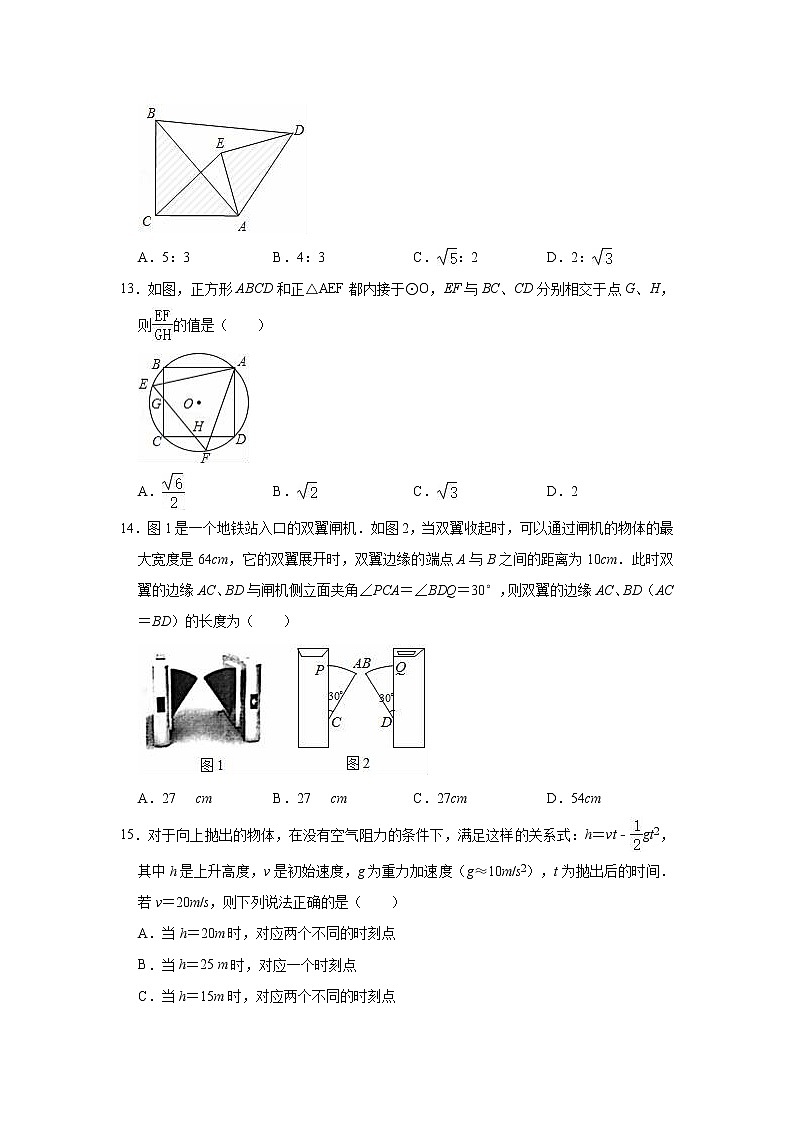
14．图1是一个地铁站入口的双翼闸机．如图2，当双翼收起时，可以通过闸机的物体的最大宽度是64cm，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm．此时双翼的边缘AC、BD与闸机侧立面夹角∠PCA＝∠BDQ＝30°，则双翼的边缘AC、BD（AC＝BD）的长度为（　　）

A．27cm B．27cm C．27cm D．54cm
15．对于向上抛出的物体，在没有空气阻力的条件下，满足这样的关系式：h＝vt﹣gt2，其中h是上升高度，v是初始速度，g为重力加速度（g≈10m/s2），t为抛出后的时间．若v＝20m/s，则下列说法正确的是（　　）
A．当h＝20m时，对应两个不同的时刻点
B．当h＝25 m时，对应一个时刻点
C．当h＝15m时，对应两个不同的时刻点
D．h取任意值，均对应两个不同的时刻点
16．如图，在矩形ABCD中，已知AB＝8，BC＝6，矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续旋转90°至图②位置，依类类推，这样连续旋转101次后顶点A在整个旋转过程中所经过的路程之和是（　　）

A．288π B．294π C．304π D．396π
二．填空题（共4小题，满分12分，每小题3分）
17．在三角形ABC中，∠C＝90°，∠A，∠B，∠C对应的边分别是a，b，c，其中a﹣b＝2，CD⊥AB于D，BD﹣AD＝2，则边c的长度为　 　．
18．如图，在△ABC中，∠A＝68°，若点O是△ABC的外心，则∠BOC＝　 　；若点O是△ABC的内心，则∠BOC＝　 　．

19．如图，已知直线l：y＝﹣x+b（b＜0）与x，y轴分别交于A，B两点，以AB为边在直线l的上方作正方形ABCD，反比例函数y1＝和y2＝的图象分别过点C和点D．若k1＝3，则k2的值为　 　．

20．如图所示，二次函数y＝ax2+bx+c的图象开口向上，图象经过点（﹣1，2）和（1，0）且与y轴交于负半轴．给出四个结论：①a+b+c＝0，②abc＜0；③2a+b＞0；④a+c＝1；
其中正确的结论的序号是　 　

三．解答题（共6小题，满分66分）
21．（10分）已知关于x的方程x2+4x+3﹣a＝0．
（1）若此方程有两个不相等的实数根，求a的取值范围；
（2）在（1）的条件下，当a取满足条件的最小整数，求此时方程的解．
22．（10分）某小区开展了“行车安全，方便居民”的活动，对地下车库作了改进．如图，这小区原地下车库的入口处有斜坡AC长为13米，它的坡度为i＝1：2.4，AB⊥BC，为了居民行车安全，现将斜坡的坡角改为13°，即∠ADC＝13°（此时点B、C、D在同一直线上）．

（1）求这个车库的高度AB；
（2）求斜坡改进后的起点D与原起点C的距离（结果精确到0.1米）．
（参考数据：sin13°≈0.225，cos13°≈0.974，tan13°≈0.231，cot13°≈4.331）
23．（10分）某中学举行“中国梦，我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学生的成绩分为A、B、C、D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题．

（1）参加比赛的学生人数共有　 　名，在扇形统计图中，表示“D等级”的扇形的圆心角为　 　度，图中m的值为　 　；
（2）补全条形统计图；
（3）组委会决定分别从本次比赛中获得A、B两个等级的学生中，各选出1名学生培训后搭档去参加市中学生演讲比赛，已知甲的等级为A，乙的等级为B，求出同时选中甲和乙的概率．
24．（12分）如图，一次函数y＝x+b的图象与y轴交于点B（0，2），与反比例函数y＝（x＜0）的图象交于点D．以BD为对角线作矩形ABCD，使顶点A、C落在x轴上（点A在点C的右边），BD与AC交于点E．
（1）求一次函数的解析式；
（2）求点D的坐标和反比例函数的解析式；
（3）求点A的坐标．

25．（12分）如图，在△ABC中，∠ABC＝∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB＝2∠BCP．
（1）求证：直线CP是⊙O的切线．
（2）若BC＝2，sin∠BCP＝，求点B到AC的距离．
（3）在第（2）的条件下，求△ACP的周长．

26．（12分）如图，已知抛物线y＝ax2+bx﹣3的图象与x轴交于点A（1，0）和B（3，0），与y轴交于点C．D是抛物线的顶点，对称轴与x轴交于E．
（1）求抛物线的解析式；
（2）如图1，在抛物线的对称轴DE上求作一点M，使△AMC的周长最小，并求出点M的坐标和周长的最小值．
（3）如图2，点P是x轴上的动点，过P点作x轴的垂线分别交抛物线和直线BC于F、G．设点P的横坐标为m．是否存在点P，使△FCG是等腰三角形？若存在，直接写出m的值；若不存在，请说明理由．


参考答案与试题解析
一．选择题（共16小题，满分42分）
1．解：方程整理得：x（x﹣4）＝0，
可得x＝0或x﹣4＝0，
解得：x1＝0，x2＝4，
故选：C．
2．解：七个数从小到大排列处在中间位置的数，
与将排序后的七个数去掉一个最大值和一个最小值而剩下的5个数中间位置的数是同一个数，
因此中位数不可能改变，
故选：A．
3．解：根据题意得：，
解得：m＝1．
故选：D．
4．解：∵二次函数y＝kx2﹣6x+3的图象与x轴有交点，
∴方程kx2﹣6x+3＝0（k≠0）有实数根，
即△＝36﹣12k≥0，k≤3，由于是二次函数，故k≠0，则k的取值范围是k≤3且k≠0．
故选：D．
5．解：从几何体左面看得到是矩形的组合体，且长方形靠左．
故选：A．
6．解：∵∠DBC＝∠A，∠C＝∠C，
∴△CBD∽△CAB，
∴，即，
∴CD＝2，
∴AD＝AC﹣CD＝3﹣2＝1．
故选：B．
7．解：∵PA是圆的切线．
∴∠OAP＝90°，
同理∠OBP＝90°，
根据四边形内角和定理可得：
∠AOB＝360°﹣∠OAP﹣∠OBP﹣∠P＝360°﹣90°﹣90°﹣40°＝140°，
∴∠ACB＝∠AOB＝70°．
故选：C．

8．解：圆锥的底面周长为2π×4＝8πcm，即为展开图扇形的弧长，
由弧长公式得＝8π，
解得，R＝12，即圆锥的母线长为12cm．
故选：B．
9．解：∵点A（﹣2020，y1），B（2021，y2）两点在双曲线y＝上，且y1＞y2，
∴3+2a＜0，
∴a＜﹣，
∴a的取值范围是a＜﹣，
故选：D．
10．解：∵抛物线y＝x2+bx+4的顶点在x轴上，
∴＝0，
解得b＝±4，
故选：D．
11．解：∵一次函数y＝x+a（a≠0），
∴一次函数图象y随x增大而增大，
故A，D不符合题意；
在B中，反比例函数过一、三象限，故a＞0，一次函数过一、三、四象限，故a＜0，不合题意；
在C中，反比例函数过一、三象限，故a＞0，一次函数过一、二、四象限，故a＞0，符合题意；
故选：C．
12．解：∵∠ACB＝∠AED＝90°，∠ABC＝∠ADE，
∴△ABC∽△ADE，
∴∠BAC＝∠DAE，，
∵∠BAC+∠BAE＝∠DAE+∠BAE，
即∠CAE＝∠BAD，
∵，
∴△ACE∽△ABD，
∴，
∵AC：BC＝3：4，∠ACB＝∠AED＝90°，
∴AC：BC：AB＝3：4：5，
∴BD：CE＝5：3，
故选：A．
13．解：如图，连接AC、BD、OF，，
设⊙O的半径是r，
则OF＝r，
∵AO是∠EAF的平分线，
∴∠OAF＝60°÷2＝30°，
∵OA＝OF，
∴∠OFA＝∠OAF＝30°，
∴∠COF＝30°+30°＝60°，
∴FI＝r•sin60°＝，
∴EF＝，
∵AO＝2OI，
∴OI＝，CI＝r﹣＝，
∴，
∴，
∴＝，
即则的值是．
故选：C．
14．解：如图，过A作AE⊥CP于E，过B作BF⊥DQ于F，

∵点A与B之间的距离为10cm，可以通过闸机的物体的最大宽度是64cm，
∴AE＝BF＝（64﹣10）÷2＝27（cm），
在Rt△ACE中，AC＝2AE＝27×2＝54（cm），
故选：D．
15．解：∵h＝vt﹣gt2，v＝20m/s，g≈10m/s2，
∴h＝20t﹣5t2
＝﹣5（t2﹣4t）
＝﹣5（t﹣2）2+20，
∴当t＝2s时，h有最大值为20m，即物体能达到的最大高度为20m，且h＝20m时，只有一个时刻，
∴A、B、D均不正确．
∵h＝20t﹣5t2为开口向下的二次函数，h有最大值为20m，
∴当h＝15m时，对应两个不同的时刻点．
∴C正确．
故选：C．
16．解：如图，

由题意可知，顶点A在连续旋转过程中，以每4次为一个循环，在一个循环中，所经过的路程之和为的长度之和，
连接A1C1，A2C1，
∵四边形ABCD是矩形，AB＝8，BC＝6，
∴∠BAD＝∠ABC＝∠BCD＝∠ADC＝90°，AD＝BC＝6，CD＝AB＝8，
由旋转的性质得：A1B＝AB＝8，A2D2＝BC1＝BC＝6，∠A1C1A2＝∠A2D2A3＝90°，
∴，
∴的长度为，的长度为，的长度为，
则在一个循环中，顶点A所经过的路程之和为4π+5π+3π＝12π，
∵101＝4×25+1，
∴所求的路程之和为25个循环的路程之和加上的长度，即25×12π+4π＝304π，
故选：C．
二．填空题（共4小题，满分12分，每小题3分）
17．解：设AB＝c，CD＝h
BD＝a×sinA＝a×，AD＝b×cosA＝b×，
BD﹣AD＝
a﹣b＝2，a+b＝（）×c
两边同时平方得：c2+2ab＝c2
∴2ab＝c2，
∵ab＝ch，
∴ab＝ch＝c2，
∴4h＝c
a2+b2﹣2ab＝8
c2﹣2ch＝8
c2﹣c2＝8
c＝4
故答案为：4

18．解：若点O是△ABC的外心，
则∠BOC＝2∠BAC＝2×68°＝136°；
若点O是△ABC的内心，
则∠BOC＝90°+∠BAC＝90°+×68°＝124°；
故答案为：136°；124°．
19．解：如图，作CH⊥y轴于点H，
∵四边形ABCD为正方形，
∴AB＝BC，∠AOB＝∠BHC＝90°，∠ABC＝90°
∴∠BAO＝90°﹣∠OBA＝∠CBH，
∴△BAO≌△CBH（AAS），
∴OA＝BH，OB＝CH，
∵直线l：y＝﹣x+b（b＜0）与x，y轴分别交于A，B两点，
∴A（3b，0），B（0，b），
∵b＜0，
∴BH＝﹣3b，CH＝﹣b，
∴点C的坐标为（﹣b，﹣2b），
同理，点D的坐标为（2b，﹣3b），
∵k1＝3，
∴（﹣b）×（﹣2b）＝3，即2b2＝3，
∴k2＝2b×（﹣3b）＝﹣6b2＝﹣9．
故答案为：﹣9．

20．解：①∵点（1，0）在二次函数图象上，
∴a+b+c＝0，结论①正确；
②∵二次函数y＝ax2+bx+c的图象开口向上，对称轴在y轴右侧，与y轴交于负半轴，
∴a＞0，﹣＞0，c＜0，
∴b＜0，
∴abc＞0，结论②错误；
③∵﹣＜1，a＞0，
∴2a＞﹣b，
∴2a+b＞0，结论③正确；
④∵二次函数y＝ax2+bx+c的图象经过点（﹣1，2）和（1，0），
∴a﹣b+c＝2，a+b+c＝0，
∴a+c＝1，结论④正确．
综上所述，正确的结论有①③④．
故答案为：①③④．
三．解答题（共6小题，满分66分）
21．解：（1）∵方程x2+4x+3﹣a＝0有两个不相等的实数根，
∴Δ＝42﹣4×1×（3﹣a）＝4+4a＞0，
解得：a＞﹣1．
（2）根据题意得：a＝0，
此时原方程为x2+4x+3＝0，即（x+1）（x+3）＝0，
解得：x1＝﹣1，x2＝﹣3．
22．解：（1）由题意，得：∠ABC＝90°，i＝1：2.4，
在Rt△ABC中，i＝＝，
设AB＝5x，则BC＝12x，
∴AB2+BC2＝AC2，
∴AC＝13x，
∵AC＝13，
∴x＝1，
∴AB＝5，
答：这个车库的高度AB为5米；

（2）由（1）得：BC＝12，
在Rt△ABD中，cot∠ADC＝，
∵∠ADC＝13°，AB＝5，
∴DB＝5cot13°≈21.655（m），
∴DC＝DB﹣BC＝21.655﹣12＝9.655≈9.7（米），
答：斜坡改进后的起点D与原起点C的距离为9.7米．
23．解：（1）根据题意得：3÷15%＝20（人），
表示“D等级”的扇形的圆心角为×360°＝72°；
C级所占的百分比为×100%＝40%，
故m＝40，
故答案为：20，72，40．

（2）等级B的人数为20﹣（3+8+4）＝5（人），
补全统计图，如图所示：
；

（3）列表如下：

乙
B
B
B
B
甲
甲、乙
甲、B
甲、B
甲、B
甲、B
A
A、乙
A、B
A、B
A、B
A、B
A
A、乙
A、B
A、B
A、B
A、B
所有等可能的结果有15种，同时选中甲和乙的情况有1种，
所以同时选中甲和乙的概率为．
24．解：（1）∵一次函数y＝x+b的图象与y轴交于点B（0，2），
∴b＝2，
∴一次函数的解析式为y＝x+2；

（2）作DF⊥x轴于F，

∵B（0，2），
∴OB＝2，
当y＝x+2＝0时，解得x＝﹣，
∴E点坐标（﹣，0），
∴OE＝，
∵四边形ABCD是矩形，
∴BE＝ED，
∵DF⊥x轴，BO⊥x轴，
∴∠DFE＝∠BOE＝90°，
∵∠DEF＝∠BEO，
∴△DEF≌△BEO（AAS），
∴OB＝DF＝2，EF＝OE＝，
∴OF＝OE+EF＝3，
∴D（﹣3，﹣2），
∵点D在反比例函数y＝的图象上，
∴k＝6，
故y＝；

（3）在Rt△BOE中，BE＝＝＝，
在矩形ABCD中，BE＝BD，AE＝AC，BD＝AC，
∴AE＝BE＝，
∴OA＝AE﹣EO＝﹣＝1，
∴A（1，0）．
25．解：（1）∵∠ABC＝∠ACB且∠CAB＝2∠BCP，在△ABC中，∠ABC+∠BAC+∠BCA＝180°
∴2∠BCP+2∠BCA＝180°，
∴∠BCP+∠BCA＝90°，
又C点在直径上，
∴直线CP是⊙O的切线．

（2）如右图，作BD⊥AC于点D，
∵PC⊥AC
∴BD∥PC
∴∠PCB＝∠DBC
∵BC＝2，sin∠BCP＝，
∴sin∠BCP＝sin∠DBC＝＝＝，
解得：DC＝2，
∴由勾股定理得：BD＝4，
∴点B到AC的距离为4．

（3）如右图，连接AN，
∵AC为直径，
∴∠ANC＝90°，
∴Rt△ACN中，AC＝＝5，
又CD＝2，
∴AD＝AC﹣CD＝5﹣2＝3．
∵BD∥CP，
∴，
∴CP＝．
在Rt△ACP中，AP＝＝，
AC+CP+AP＝5++＝20，
∴△ACP的周长为20．

26．解：（1）将点A、B的坐标代入抛物线表达式得：，
解得，
∴抛物线的解析式为：y＝﹣x2+4x﹣3；

（2）如下图，连接BC交DE于点M，此时MA+MC最小，

又因为AC是定值，所以此时△AMC的周长最小．
由题意可知OB＝OC＝3，OA＝1，
∴BC＝＝3，同理AC＝，
∴此时△AMC的周长＝AC+AM+MC＝AC+BC＝+3；
∵DE是抛物线的对称轴，与x轴交点A（1，0）和B（3，0），
∴AE＝BE＝1，对称轴为 x＝2，
由OB＝OC，∠BOC＝90°得∠OBC＝45°，
∴EB＝EM＝1，
又∵点M在第四象限，在抛物线的对称轴上，
∴M（2，﹣1）；

（3）存在这样的点P，使△FCG是等腰三角形．
∵点P的横坐标为m，故点F（m，﹣m2+4m﹣3），点G（m，m﹣3），
则FG2＝（﹣m2+4m﹣3+3﹣m）2，CF2＝（m2﹣4m）2+m2，GC2＝2m2，
当FG＝FC时，则（﹣m2+4m﹣3+3﹣m）2＝m2+（m2﹣4m）2，解得m＝0（舍去）或4；
当GF＝GC时，同理可得m＝0（舍去）或3；
当FC＝GC时，同理可得m＝0（舍去）或5或3（舍去），
综上，m＝5或m＝4或或3．