浙江省宁波市江北区2021-2022学年九年级上学期期末数学模拟试卷（word版 含答案）

这是一份浙江省宁波市江北区2021-2022学年九年级上学期期末数学模拟试卷（word版 含答案），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
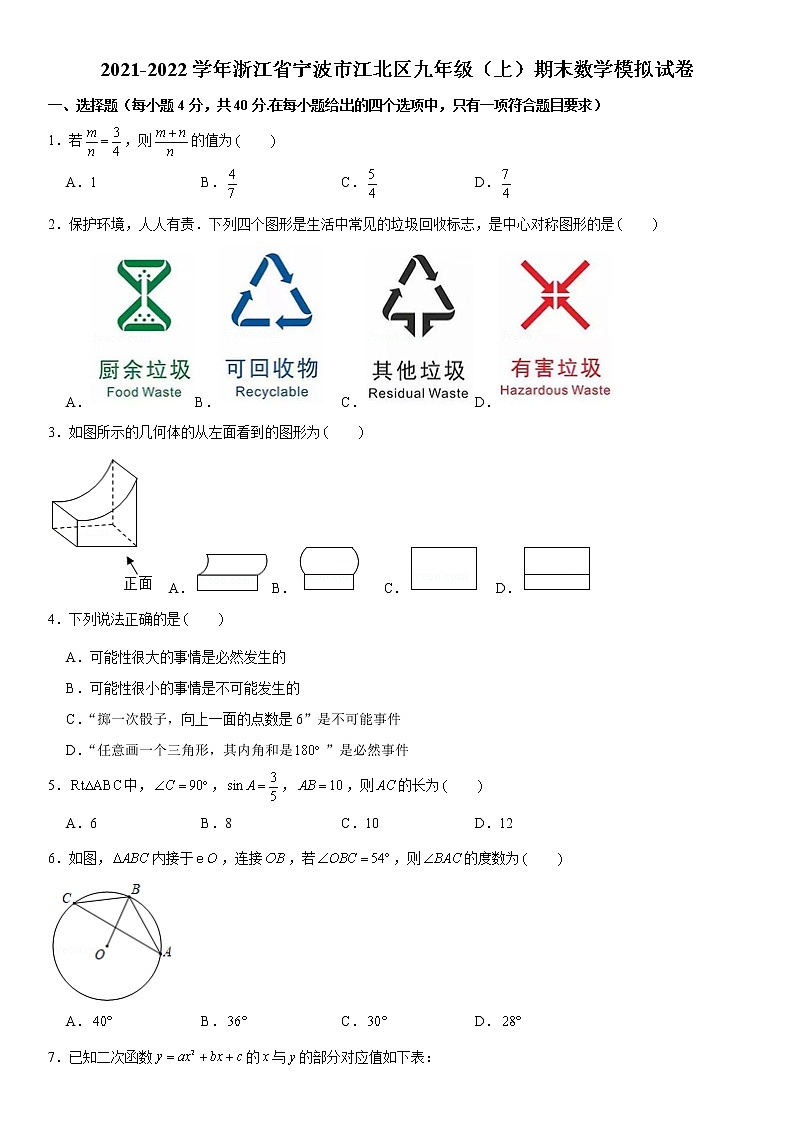
2021-2022学年浙江省宁波市江北区九年级（上）期末数学模拟试卷一、选择题（每小题4分，共40分.在每小题给出的四个选项中，只有一项符合题目要求）1．若，则的值为　　A．1 B． C． D．2．保护环境，人人有责．下列四个图形是生活中常见的垃圾回收标志，是中心对称图形的是　　A．B． C．D．3．如图所示的几何体的从左面看到的图形为　　  A． B． C． D．4．下列说法正确的是　　A．可能性很大的事情是必然发生的 B．可能性很小的事情是不可能发生的 C．“掷一次骰子，向上一面的点数是6”是不可能事件 D．“任意画一个三角形，其内角和是”是必然事件5．中，，，，则的长为　　A．6 B．8 C．10 D．126．如图，内接于，连接，若，则的度数为　　A． B． C． D．7．已知二次函数的与的部分对应值如下表：01335下列结论：①；②函数的最大值为5；③方程的解为，；④当时，．其中正确结论的个数是　　A．4 B．3 C．2 D．18．平行四边形如图所示，为上的一点，、分别为与、的交点．若，则四边形与的面积之比为　　A． B． C． D．9．如图，在中，，，，的半径为2，圆心在边上运动，当与的边恰有4个交点时，的取值范围是　　A． B．或 C． D．或10．如图，的半径为4，直径与直径垂直，是上一点，连接，分别交，于，，若，则的长为　　A． B． C． D．二、填空题（每小题5分，共30分）11．一个不透明的口袋中装有2个红球和若干个白球，它们除颜色外其它完全相同．通过多次摸球试验后发现，摸到红球的频率稳定在附近，口袋中白球最有可能有 　　个．12．某同学在数学实践活动中，制作了一个侧面积为，底面半径为6的圆锥模型（如图所示），则此圆锥的母线长为 　　．13．抛物线的对称轴是　　．14．如图，，、均为的切线，，，分别是切点，，则的周长为　 　．15．如图，在中，为的直径，，于，，则　　．16．在中，，，，点是斜边上一动点，从点向点运动，过点作，垂足为，交边（或边于点，设，当的面积为时，的值为　　．三、解答题（第17-19题各8分，第20～22题各10分，第23题12分，第24题14分，共80分）17．计算：． 18．文物探测队探测出某建筑物下面有地下文物，为了准确测出文物所在的具体位置，他们在文物上方建筑物的一侧地面上相距20米的、两处，用仪器测文物，探测线与地面的夹角分别为和．（1）求的度数；（2）求的长．19．越野汽车轮胎的质量是根据其正常使用的时间来衡量，使用时间越长，表明质量越好，且使用时间大于或等于7千小时的为优质品，否则为普通品．某汽修店对，两种不同型号的汽车轮胎做试验，各随机抽取部分产品作为样本，得到试验结果的扇形统计图和折线图如图所示：根据上述调查数据，解决下列问题：（1）现从仓库中大量的，两种型号的轮胎中各随机抽取1件产品，求其中至少有1件是优质品的概率；（2）汽修店对轮胎实行“三包”，根据多年销售经验可知，轮胎每件产品的利润（单位：元）与其使用时间（单位：千小时）的关系如下表：使用时间（单位：千小时）每件产品的利润（单位：元）200400请从平均利润角度考虑，该汽修店应选择销售哪种轮胎，说明理由．    20．图1是由六个全等且边长为2的小正五边形，以及五个全等且顶角为、腰长为2的等腰三角形镶嵌而成的一个大正五边形，正五边形和等腰三角形的顶点称为格点，连接格点而成的三角形称为格点三角形．在图2的三个图中，分别画出一个与图中已知相似但不全等的格点三角形，并注明三角形的顶点字母． 21．在平面直角坐标系中，二次函数图象的顶点为，且经过点．（1）求该二次函数的解析式；（2）将该二次函数图象向右平移使平移后所得图象经过坐标原点，请直接写出平移后所得图象与轴的另一个交点的坐标．22．如图，内接于，为直径，的平分线交于点，作交的延长线于点．（1）求证：；（2）求证：是的切线；（3）若，，求弦的长． 23．疫情期间，某销售商在网上销售、两种型号的电脑“手写板”，其进价、售价和每日销量如表所示： 进价（元个）售价（元个）销量（个日）型400600200型8001200400根据市场行情，该销售商对型手写板降价销售，同时对型手写板提高售价，此时发现型手写板每降低5元就可多卖1个，型手写板每提高5元就少卖1个．销售时保持每天销售总量不变，设其中型手写板每天多销售个，每天获得的总利润为元．（1）求与之间的函数关系式，并直接写出的取值范围；（2）要使每天的利润不低于212000元，求出的取值范围；（3）该销售商决定每销售一个型手写板，就捐助元给受“新冠疫情”影响的困难学生，若当时，每天的最大利润为203400元，求的值．    24．如图，是的直径，点是上一点，过点作弦于，点是上一点，交于点，过点作一条直线交的延长线于，交的延长线于，．（1）求证：是的切线；（2）若，试探究，，之间的关系，并说明理由；（3）在（2）的条件下，若，，求的长．
2021-2022学年浙江省宁波市江北区九年级（上）期末数学模拟试卷参考答案与试题解析一、选择题（每小题4分，共40分.在每小题给出的四个选项中，只有一项符合题目要求）1．若，则的值为　　A．1 B． C． D．【解答】解：，设，则，则．故选：．2．保护环境，人人有责．下列四个图形是生活中常见的垃圾回收标志，是中心对称图形的是　　A． B． C． D．【解答】解：、是轴对称图形，不是中心对称图形．故本选项不符合题意；、不是轴对称图形，不是中心对称图形．故本选项不符合题意；、不是轴对称图形，不是中心对称图形．故本选项不符合题意；、既是轴对称图形又是中心对称图形．故本选项符合题意．故选：．3．如图所示的几何体的从左面看到的图形为　　A． B． C． D．【解答】解：从这个几何体的左面看，所得到的图形是长方形，能看到的轮廓线用实线表示，看不见的轮廓线用虚线表示，因此，选项的图形，符合题意，故选：．4．下列说法正确的是　　A．可能性很大的事情是必然发生的 B．可能性很小的事情是不可能发生的 C．“掷一次骰子，向上一面的点数是6”是不可能事件 D．“任意画一个三角形，其内角和是”是必然事件【解答】解：、可能性很大的事情也可能不会发生，故错误，不符合题意；、可能性很小的事情是也可能发生的，故错误，不符合题意；、掷一次骰子，向上一面的点数是6”是随机事件，故错误，不符合题意；、“任意画一个三角形，其内角和是”，正确，符合题意，故选：．5．中，，，，则的长为　　A．6 B．8 C．10 D．12【解答】解：在中，，，，，，，故选：．6．如图，内接于，连接，若，则的度数为　　A． B． C． D．【解答】解：如图，连接，，，，．故选：．7．已知二次函数的与的部分对应值如下表：01335下列结论：①；②函数的最大值为5；③方程的解为，；④当时，．其中正确结论的个数是　　A．4 B．3 C．2 D．1【解答】解：由点的特征可知，故①正确；时，，，当时取到最大值，最大值为5，故②正确；时，，，对称轴为直线，当时，，，故③正确；由表格可知抛物线顶点，设抛物线，将代入，得，故，令，则，解得：，当时，，当时，，故④错误，故选：．8．平行四边形如图所示，为上的一点，、分别为与、的交点．若，则四边形与的面积之比为　　A． B． C． D．【解答】解：，，，四边形是平行四边形，，，，，设，，，，，，，，四边形与的面积之比为，故选：．9．如图，在中，，，，的半径为2，圆心在边上运动，当与的边恰有4个交点时，的取值范围是　　A． B．或 C． D．或【解答】解：，，，，如图1，当过点时，此时与的边恰有3个交点，此时，当过点时，此时与的边恰有3个交点，此时，则；如图2，当与相切于点时，此时与的边恰有3个交点，连接，，，又，，，，，当与相切于点时，此时与的边恰有3个交点，同理可求，，当与的边恰有4个交点时，的取值范围为或．故选：．10．如图，的半径为4，直径与直径垂直，是上一点，连接，分别交，于，，若，则的长为　　A． B． C． D．【解答】解：连接，过点作于．，，，，，，，，设，则，，，，，，，，，．故选：．二、填空题（每小题5分共30分）11．一个不透明的口袋中装有2个红球和若干个白球，它们除颜色外其它完全相同．通过多次摸球试验后发现，摸到红球的频率稳定在附近，口袋中白球最有可能有 　8　个．【解答】解：设口袋中白球可能有个，摸到红球的频率稳定在附近，口袋中摸到红色球的概率为，，解得：，经检验是原方程的根，故答案为：8．12．某同学在数学实践活动中，制作了一个侧面积为，底面半径为6的圆锥模型（如图所示），则此圆锥的母线长为 　10　．【解答】解：设此圆锥的母线长为，根据题意得，解得，所以此圆锥的母线长为10．故答案为10．13．抛物线的对称轴是　直线　．【解答】解：抛物线，该抛物线对称轴是直线，故答案为：直线．14．如图，，、均为的切线，，，分别是切点，，则的周长为　16　．【解答】解：，、均为的切线，，，分别是切点，，，，的周长，的周长，，的周长为16．15．如图，在中，为的直径，，于，，则　　．【解答】解：如图，连接．，，是直径，，，，，，，，，，，故答案为：．16．在中，，，，点是斜边上一动点，从点向点运动，过点作，垂足为，交边（或边于点，设，当的面积为时，的值为　或14　．【解答】解：当点在边上时，如图所示：，，，，，，解得：，（舍去）；当点在边上时，如图所示：，，，，又，，，在中，，，，，，，，，，，解得：（舍，，综上所述，的值为或14．三、解答题（第17-19题各8分，第20～22题各10分，第23题12分，第24题14分，共80分）17．计算：．【解答】解：原式．18．文物探测队探测出某建筑物下面有地下文物，为了准确测出文物所在的具体位置，他们在文物上方建筑物的一侧地面上相距20米的、两处，用仪器测文物，探测线与地面的夹角分别为和．（1）求的度数；（2）求的长．【解答】解：（1）由题意可得：； （2）过点作于点，可得：，，，，，，解得：，答：的长为．19．越野汽车轮胎的质量是根据其正常使用的时间来衡量，使用时间越长，表明质量越好，且使用时间大于或等于7千小时的为优质品，否则为普通品．某汽修店对，两种不同型号的汽车轮胎做试验，各随机抽取部分产品作为样本，得到试验结果的扇形统计图和折线图如图所示：根据上述调查数据，解决下列问题：（1）现从仓库中大量的，两种型号的轮胎中各随机抽取1件产品，求其中至少有1件是优质品的概率；（2）汽修店对轮胎实行“三包”，根据多年销售经验可知，轮胎每件产品的利润（单位：元）与其使用时间（单位：千小时）的关系如下表：使用时间（单位：千小时）每件产品的利润（单位：元）200400请从平均利润角度考虑，该汽修店应选择销售哪种轮胎，说明理由．【解答】解：（1）样本中，型轮胎为优质品的频率为，型轮胎为优质品的频率为，以此估计，各随机抽取一件，型轮胎，“优质品”和“普通品”这两个事件均为等可能事件．所以从仓库中大量，两种型号的轮胎中各随机抽取1件产品，产生以下“优优”，“优普”，“普优”，“普普”四种等可能结果，所以，至少有1件是优质品的概率为． （2）该汽修店应选择销售型轮胎，理由如下：对于型轮胎，列表如下：使用时间（单位：千小时）频率每件产品的利润（单位：元）200400可估计，一件型轮胎的平均利润为（元，对于型轮胎，列表如下：使用时间（单位：千小时）频率401050每件产品的利润（单位：元）200400可估计，一件型轮胎的平均利润为（元，，该汽修店应选择销售型轮胎．20．图1是由六个全等且边长为2的小正五边形，以及五个全等且顶角为、腰长为2的等腰三角形镶嵌而成的一个大正五边形，正五边形和等腰三角形的顶点称为格点，连接格点而成的三角形称为格点三角形．在图2的三个图中，分别画出一个与图中已知相似但不全等的格点三角形，并注明三角形的顶点字母．【解答】解：如图，，，即为所求．图①中，，，；图②中，，；图③中，，．21．在平面直角坐标系中，二次函数图象的顶点为，且经过点．（1）求该二次函数的解析式；（2）将该二次函数图象向右平移使平移后所得图象经过坐标原点，请直接写出平移后所得图象与轴的另一个交点的坐标．【解答】解：（1）二次函数图象的顶点为，设二次函数解析式为，把点代入二次函数解析式，得：，解得，二次函数解析式为，即； （2）令，得，解方程，得，．二次函数图象与轴的两个交点坐标分别为和，二次函数图象上的点向右平移3个单位后经过坐标原点或向右平移1个单位，故平移后所得图象与轴的另一个交点坐标为或．22．如图，内接于，为直径，的平分线交于点，作交的延长线于点．（1）求证：；（2）求证：是的切线；（3）若，，求弦的长．【解答】（1）证明：，，，，；（2）证明：连接，平分，，，，，，是的切线；（3）解：为直径，，，，，，，四边形内接于圆，，又，，，，，，，，，，，，，．23．疫情期间，某销售商在网上销售、两种型号的电脑“手写板”，其进价、售价和每日销量如表所示： 进价（元个）售价（元个）销量（个日）型400600200型8001200400根据市场行情，该销售商对型手写板降价销售，同时对型手写板提高售价，此时发现型手写板每降低5元就可多卖1个，型手写板每提高5元就少卖1个．销售时保持每天销售总量不变，设其中型手写板每天多销售个，每天获得的总利润为元．（1）求与之间的函数关系式，并直接写出的取值范围；（2）要使每天的利润不低于212000元，求出的取值范围；（3）该销售商决定每销售一个型手写板，就捐助元给受“新冠疫情”影响的困难学生，若当时，每天的最大利润为203400元，求的值．【解答】解：（1）由题意得，，且为整数），即与之间的函数关系式是，且为整数）；（2），当时，，解得：，，要使，则，，，即的取值范围是：；（3）设捐款后每天的利润为元，则，对称轴为，，，抛物线开口向下，当时，随的增大而增大，当时，最大，，解得，．24．如图，是的直径，点是上一点，过点作弦于，点是上一点，交于点，过点作一条直线交的延长线于，交的延长线于，．（1）求证：是的切线；（2）若，试探究，，之间的关系，并说明理由；（3）在（2）的条件下，若，，求的长．【解答】解：（1）证明：连接，如图：，，，，，，，，即，，是的切线；（2），理由如下：连接，如图：，，，，又，，，即，，；（3）连接、，如图：，，，，设，则，，，，，，，，，中，，，，解得或（舍去），，，设半径为，则，中，，，解得，，是的切线，，中，，，即，，．