2021学年第一章 三角函数1.1 任意角和弧度制教学设计

第三十六教时

教材：已知三角函数值求角（反正弦，反余弦函数）

目的：要求学生初步（了解）理解反正弦、反余弦函数的意义，会由已知角的正弦值、余弦值求出范围内的角，并能用反正弦，反余弦的符号表示角或角的集合。

过程：

一、简单理解反正弦，反余弦函数的意义。

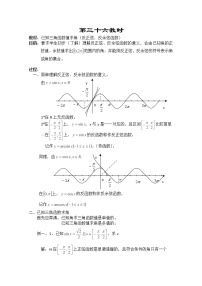
由

1在R上无反函数。

2在上， x与y是一一对应的，且区间比较简单

在上，的反函数称作反正弦函数，

记作，（奇函数）。

同理，由

在上，的反函数称作反余弦函数，

记作

二、已知三角函数求角

首先应弄清：已知角求三角函数值是单值的。

                已知三角函数值求角是多值的。

例一、1、已知，求x

解：在上正弦函数是单调递增的，且符合条件的角只有一个

          ∴（即）

2、已知

解：，是第一或第二象限角。

          即（）。

3、已知

解：x是第三或第四象限角。

（即 或 ）

这里用到是奇函数。

例二、1、已知，求

解：在上余弦函数是单调递减的，

且符合条件的角只有一个

2、已知，且，求x的值。

解：，x是第二或第三象限角。

3、已知，求x的值。

解：由上题：。

介绍：∵

∴上题

例三、（见课本P74-P75）略。

三、小结：求角的多值性

          法则：1、先决定角的象限。

                2、如果函数值是正值，则先求出对应的锐角x；

                   如果函数值是负值，则先求出与其绝对值对应的锐角x，

3、由诱导公式，求出符合条件的其它象限的角。

四、作业：P76-77 练习      3

                 习题4.11  1，2，3，4中有关部分。