必修41.5 函数y=Asin（ωx+ψ）教学设计

这是一份必修41.5 函数y=Asin（ωx+ψ）教学设计，共7页。教案主要包含了复习引入，讲授新课，典型例题，课堂练习，课堂小结，作业等内容，欢迎下载使用。
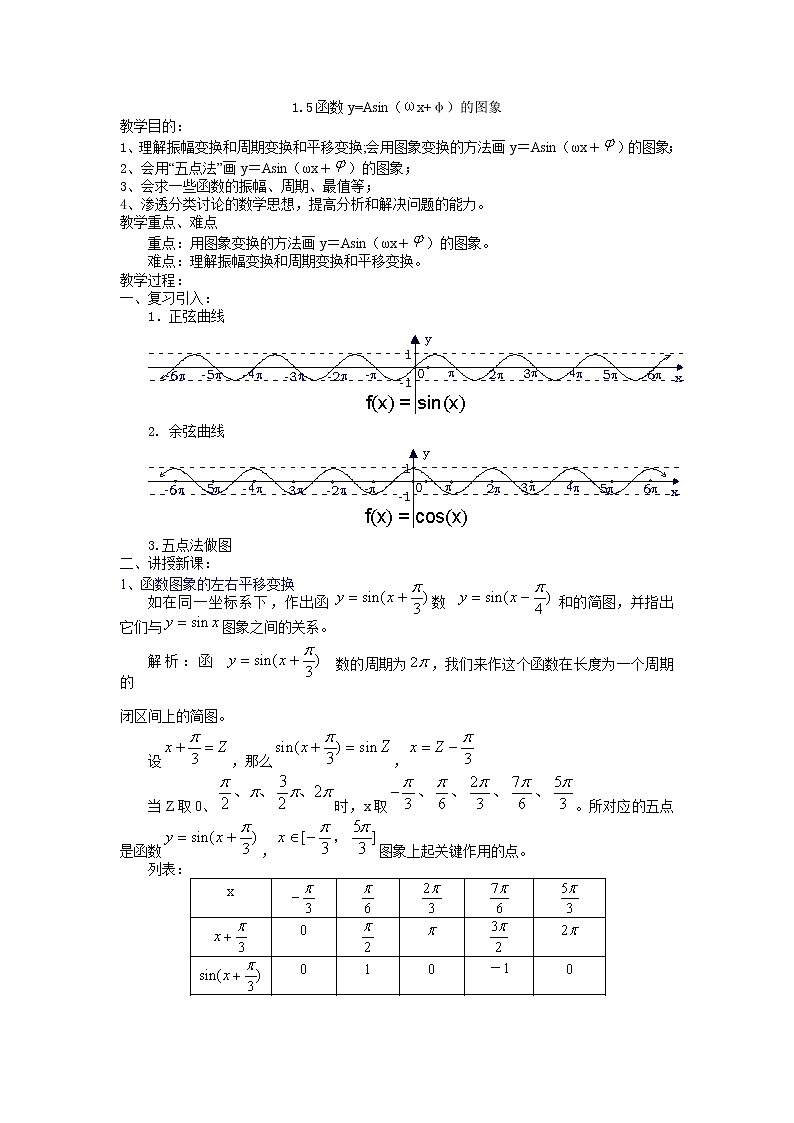
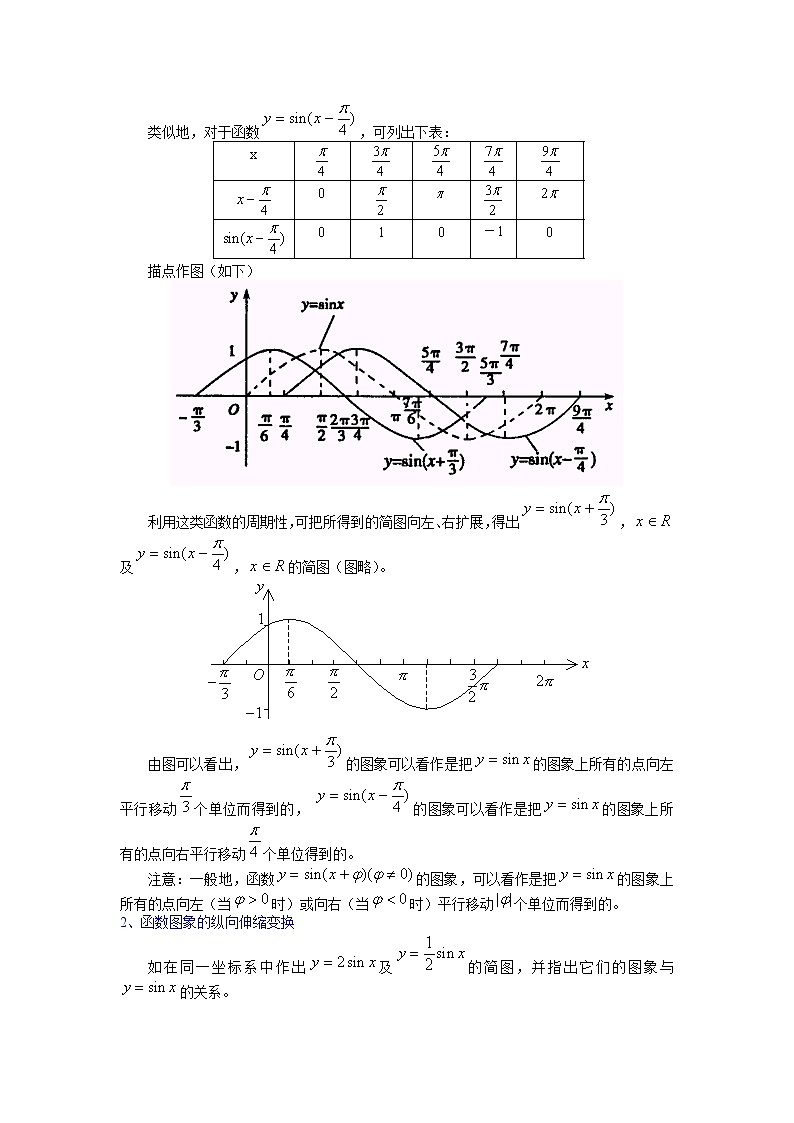
1.5函数y=Asin（ωx+φ）的图象教学目的：1、理解振幅变换和周期变换和平移变换;会用图象变换的方法画y＝Asin（ωx＋）的图象；2、会用“五点法”画y＝Asin（ωx＋）的图象；3、会求一些函数的振幅、周期、最值等；4、渗透分类讨论的数学思想，提高分析和解决问题的能力。教学重点、难点重点：用图象变换的方法画y＝Asin（ωx＋）的图象。难点：理解振幅变换和周期变换和平移变换。教学过程：一、复习引入：1．正弦曲线2. 余弦曲线3.五点法做图二、讲授新课：1、函数图象的左右平移变换    如在同一坐标系下，作出函数和的简图，并指出它们与图象之间的关系。 解析：函数的周期为，我们来作这个函数在长度为一个周期的 闭区间上的简图。    设，那么，    当Z取0、时，x取。所对应的五点是函数，图象上起关键作用的点。    列表：    类似地，对于函数，可列出下表：    描点作图（如下）    利用这类函数的周期性，可把所得到的简图向左、右扩展，得出，及，的简图（图略）。    由图可以看出，的图象可以看作是把的图象上所有的点向左平行移动个单位而得到的， 的图象可以看作是把的图象上所有的点向右平行移动个单位得到的。    注意：一般地，函数的图象，可以看作是把的图象上所有的点向左（当时）或向右（当时）平行移动个单位而得到的。2、函数图象的纵向伸缩变换    如在同一坐标系中作出及的简图，并指出它们的图象与的关系。    解析：函数及的周期，我们先来作时函数的简图。    列表：    描点作图，如图：    利用这类函数的周期性，我们可以把上图的简图向左、向右扩展，得到及的简图（图略）。    从上图可以看出，对于同一个x值，的图象上点的纵坐标等于的图象上点的纵坐标的两倍（横坐标不变），从而的值域为［－2，2］，最大值为2，最小值为－2。    类似地，的图象，可以看作是把的图象上所有点的纵坐标缩短到原来的倍（横坐标不变）而得到的，从而的值域是［］，最大值为，最小值为。    注意：对于函数（A>0且A≠1）的图象，可以看作是把的图象上所有点的纵坐标伸长（当A>1时）或缩短（当0<A<1时）到原来的A倍（横坐标不变）而得到的，的值域为［－A，A］，最大值为A，最小值为－A。3、函数图象的横向伸缩变换如作函数及的简图，并指出它们与图象间的关系。解析：函数的周期，我们来作时函数的简图。设，那么，当Z取0、时，所对应的五点是函数图象上起关键作用的五点，这里，所以当x取0、、时，所对应的五点是函数的图象上起关键作用的五点。    列表：  函数的周期，我们来作时函数的简图。     列表：    描点作图，如图：    利用这类函数的周期性，我们可以把上面的简图向左、右扩展，得出，及，的简图（图略）。    从上图可以看出，在函数的图象上横坐标为（）的点的纵坐标同上横坐标为的点的纵坐标相同（例如，当时，，）。因此，的图象可以看作是把的图象上所有点的横坐标缩短到原来的倍（纵坐标不变）而得到的。    类似地，的图象可以看作是把的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）而得到的。    注意：一般地，函数的图象，可以看作是把的图象上所有点的横坐标缩短（当时）或伸长（当时）到原来的倍（纵坐标不变）而得到的。4、函数的图象    作函数的图象主要有以下两种方法：    （1）用“五点法”作图    用“五点法”作的简图，主要是通过变量代换，设，由z取0，，，，来求出相应的x，通过列表，计算得出五点坐标，描点后得出图象。    （2）由函数的图象通过变换得到的图象，有两种主要途径：“先平移后伸缩”与“先伸缩后平移”。    法一：先平移后伸缩                法二：先伸缩后平移                可以看出，前者平移个单位，后者平移个单位。原因在于相位变换和周期变换都是针对变量x而言的。因此在用这样的变换法作图象时一定要注意平移的先后顺序，否则必然会出现错误。    当函数（A>0，，）表示一个振动量时，A就表示这个量振动时离开平衡位置的最大距离，通常把它叫做这个振动的振幅；往复振动一次所需要的时间，它叫做振动的周期；单位时间内往复振动的次数，它叫做振动的频率；叫做相位，叫做初相（即当x＝0时的相位）。三、典型例题  例1. 用两种方法将函数的图象变换为函数的图象。    分析1：    解法1：            分析2：    解法2：           注意：在解法1中，先伸缩，后平移；在解法2中，先平移，后伸缩，表面上看来，两种变换方法中的平移是不同的（即和），但由于平移时平移的对象已有所变化，所以得到的结果是一致的。   例2. 用五点法作出函数的图象，并指出函数的单调区间。       解：（1）列表    列表时取值为0、、、、，再求出相应的x值和y值。    （2）描点    （3）用平滑的曲线顺次连结各点所得图象如图所示：    利用这类函数的周期性，我们可以把上面所得到的简图向左、右扩展，得到，的简图（图略）。可见在一个周期内，函数在［］上递减，又因函数的周期为，所以函数的递减区间为。同理，增区间为。例3. 如图是函数的图象，确定A、、的值。    解：显然A＝2                解法1：由图知当时，y＝0    故有，    所求函数解析式为    解法2：由图象可知将的图象向左移    即得，即    四、课堂练习：课本62页练习第1、2、3、4、题五、课堂小结略六、作业课本第65页习题A组第1、3题     B组第2、3题