人教版新课标A必修41.4 三角函数的图象与性质学案

这是一份人教版新课标A必修41.4 三角函数的图象与性质学案，共4页。
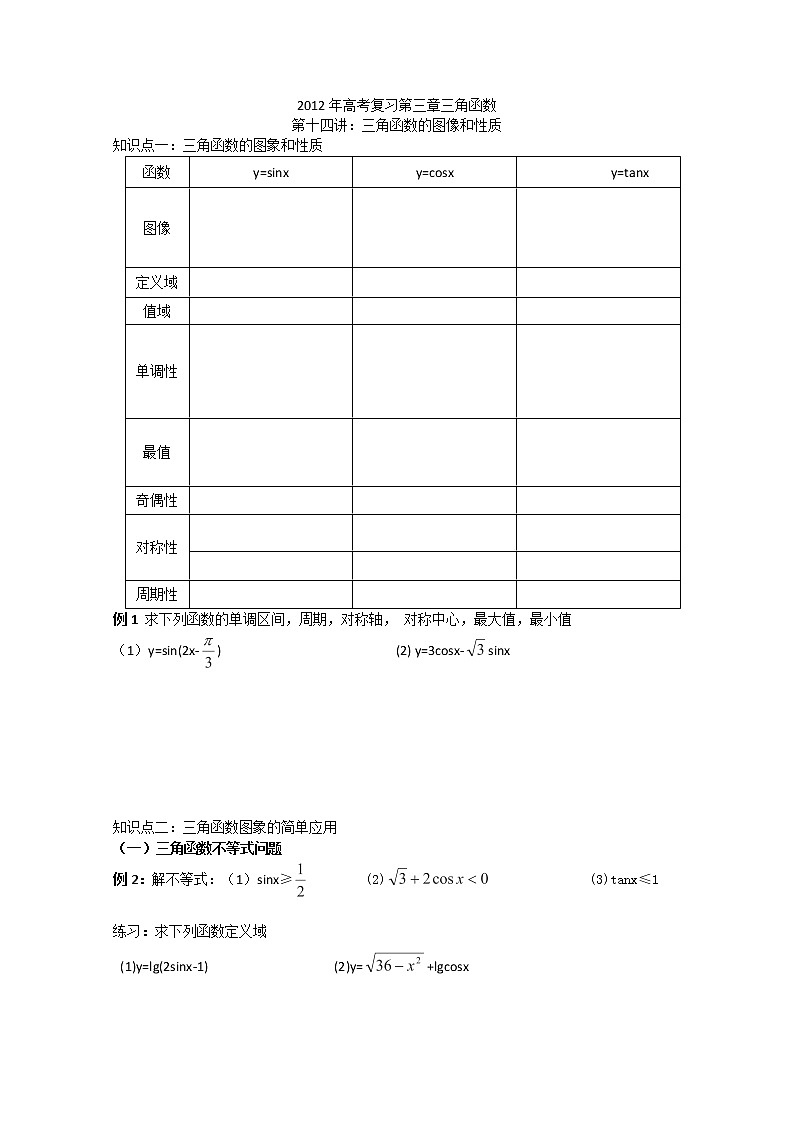
2012年高考复习第三章三角函数第十四讲：三角函数的图像和性质知识点一：三角函数的图象和性质函数y=sinxy=cosxy=tanx图像   定义域   值域   单调性   最值   奇偶性   对称性       周期性   例1 求下列函数的单调区间，周期，对称轴， 对称中心，最大值，最小值（1）y=sin(2x-)                         (2) y=3cosx-sinx       知识点二：三角函数图象的简单应用（一）三角函数不等式问题例2：解不等式：（1）sinx≥        (2)              (3)tanx≤1 练习：求下列函数定义域(1)y=lg(2sinx-1)                  (2)y=+lgcosx     （二）三角函数值域问题例3：求下列函数的最大值和最小值(1)y=2sinx+1      (2) y=-2cosx  x∈[,    (3) y=2sin(2x) +3  x∈[0,]       练习（1）求函数f(x)＝sin x +sin(+x)的最大值。    （2）函数在区间上的最大值是                 例4：函数y=sin2x+sinx-1的值域为                     练习：函数f(x)=cos2x+sinx在区间[]上的最小值是                例5： 函数的最大值和最小值      练习：求函数y=(sinx-2)(cosx-2)的值域     （三）三角函数单调性例6：求下列函数的单调区间（1）y=                          (2)y=-|cos(x+)|     例7：比较大小：sin（sin）和sin（cos）   练习：在ABC中，C>,若函数y=f(x)在[0,1]上为单调递减函数，则下列命题正确的是（   ）A f(cosA)>f (cosB)  B f(sinA)>f(sinB)  C f(sinA)>f(cosB)  D f(sinA)<f(cosB)     (四)三角函数的对称性和周期性例7 下列函数是偶函数的是                                         （    ）A   y=sinx   B  y=-sin2x   C   y=sin︱x︳D   y=sinx+1练习1 若函数f(x)=sin(2x+)是偶函数，则的一个值为                  (    )A  =     B  =-    C  =     D  =练习2：如果f(x)=sin(x+)+2cos(x+)是奇函数，则tan=               练习3 函数y=sin(2x+ ) 的图像一条对称轴方程是                     (   )A    x=-   B       C         D     例8：y=（sinx+cosx）2-1是最小正周期为           的           （奇、偶）函数练习1.函数的最小正周期是        。(五)三角函数性质的综合应用例9 已知函数f(x)是定义在R上的偶函数，且在区间[0,+∞]上是增函数，令a=f(sin)b=f(cos) c=f(tan),则a，b，c的大小关系                例10：已知函数f(x)=Asinwx+Bcoswx（A，B，w是实常数，w>0）的最小正周期为2，并且当x=时，f(x)取得最大值2.（1）求f(x)的解析式；（2）在闭区间上是否存在f(x)的对称轴？如果存在，求出其对称轴方程，如果不存在，请说明理由。         练习：已知函数f(x)= 2sinx(sinx+cosx)-1, x∈R.(1)    求函数f(x)的单调减区间  （2）求函数f(x)在区间上的最大值和最小值