人教版新课标A必修53.3 二元一次不等式（组）与简单的线性学案

巧用线性规划思想解题

　　当约束条件或目标函数不是线性规划问题，但其几何意义明显时，仍可利用线性规划的思想来解决问题，从而使解题思路拓宽，提高解题能力．

一、          函数问题转化为线性规划问题

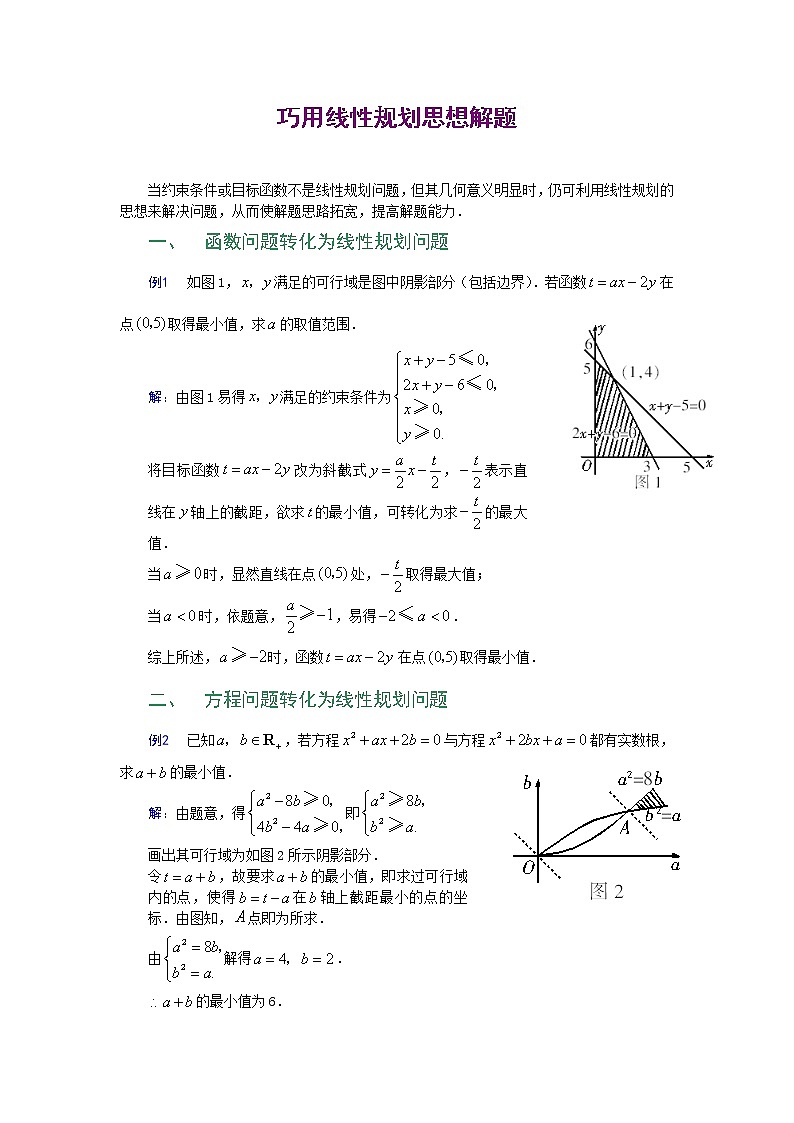
例1         如图1，满足的可行域是图中阴影部分（包括边界）．若函数在

点取得最小值，求的取值范围．

解：由图1易得满足的约束条件为

将目标函数改为斜截式，表示直线在轴上的截距，欲求的最小值，可转化为求的最大值．

当时，显然直线在点处，取得最大值；

当时，依题意，，易得．

综上所述，时，函数在点取得最小值．

二、          方程问题转化为线性规划问题

例2         已知，若方程与方程都有实数根，

求的最小值．

解：由题意，得即

画出其可行域为如图2所示阴影部分．

令，故要求的最小值，即求过可行域内的点，使得在轴上截距最小的点的坐标．由图知，点即为所求．

由解得．

的最小值为6．

三、          不等式问题转化为线性规划问题

例3         已知，且，，求的取值范围．

解：如图3，作出不等式组

所表示的平面区域，即可行域．

作直线，把直线向右下方平移过，即直线与

的交点时，；

再把直线向右下方平移过即直线与的交点时，，．

说明：本题还可运用整体代换法，先用与的一次组合表示，找出它们之间

的线性关系，然后利用不等式的性质加以解决．

四、          多元问题转化为线性规划问题

例4         已知的三边长满足，，求的取值范围．

解：由题意，应用

令，

上述不等式可化为

求出的范围即可．

作出可行域如图4，易得，

于是的范围为．

实 际 问 题 中 的 易 错 点

　　在解决线性规划中的一些实际问题时，我们对整数点往往寻找的不正确．出现这种子错误的原因是由于我们画图不准确或都是没有考虑到实际问题的特殊性．下面，我们就一道例题来剖析在解决实际问题时容易出现的一些错误及如何寻找整数点．

　　例　有一批钢管，长度都是4000mm，要截成500mm和600mm两种毛坯，且这两种数量比大于，要使钢管截得的毛坯最多，问怎样截最合理？

　　误：设截500mm的根，600mm的根，则满足的约束条件为

即

其中均为整数．

作出可行域，如图1中阴影部分所示．

目标函数为．作一组平行直线，经过可行域内的点且和原点距离最远的直线为过点的直线，先求出点的坐标．

解得．

即为，又由于均为正整数，故调整为．

经检验满足条件，所以每根钢管截500mm的毛坯两根，600mm的毛坯五根最合理．

析：本题的错误主要是在作一组平行直线时，没能准确作出，而得到可行域内的点且和原点距离最远的直线为过点的直线．

此错误可检验如下：

如果直线通过点时是可行域内的点到原点的距离最远的直线，那么，即．由于为整数，因此点不是最优解，则需调整点，但在可行域内除点外不可能再有其它点满足，只能在可行域内找满足的整数点．但我们知道满足题意．这样，就会出现矛盾，从而判断解法错误，即通过点心并不是可行域内的点且和原点距离最远的直线．

　　正：设截500mm的毛坯根，600mm根的毛坯根．

　　根据题意，得且均为正整数．

　　作出可行域，如图2中阴影部分．

　　目标函数为，作一组平行直线，经过可行域为的点且和原点距离最远的直线必为过点的直线（在此时，有的同学由于没有考虑到实际问题的特殊性，所以会误认为是最优整数解）．

　　这时．

　　为正整数，不是最优解．

　　在可行域内找整点，使．

　　经验证，可知点均为最优解．

　　答：每根钢管截500mm的两根600mm的五根，或截500mm的三根600mm的四根，或截500mm的四根，600mm的三根，或截500mm的五根600mm的两根，或截500mm的六根600mm的一根最合理．

　　评注：在可行域内找整点最优解，一般采用平移找解法，即打网格、描整点、平移直线，找出最优解．