人教版八年级上册第十三章 轴对称综合与测试复习课件ppt

这是一份人教版八年级上册第十三章 轴对称综合与测试复习课件ppt，共42页。PPT课件主要包含了二线段的垂直平分线，x1x2，y22n-y1，利用轴对称变换作图，课堂练习等内容，欢迎下载使用。
把一个图形沿着一条直线折叠，如果直线两旁的部分能够互相重合，那么这个图形就叫做轴对称图形。这条直线就是它的对称轴。这时我们也说这个图形关于这条直线（成轴）对称。 把一个图形沿着某一条直线折叠，如果它能与另一个图形重合，那么就说这两个图形关于这条直线（成轴）对称。这条直线叫做对称轴。折叠后重合的点是对应点,叫做对称点.
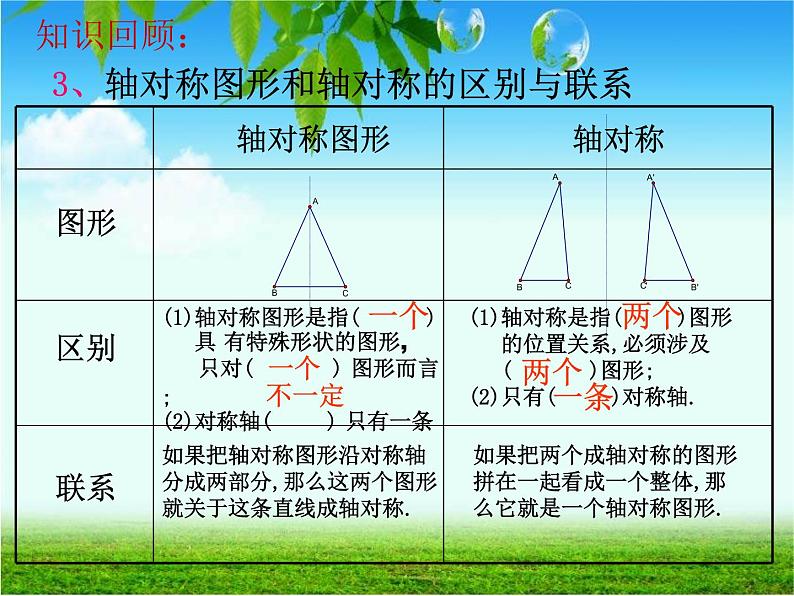
3、轴对称图形和轴对称的区别与联系
(1)轴对称图形是指( ) 具 有特殊形状的图形, 只对( ) 图形而言;(2)对称轴( ) 只有一条
(1)轴对称是指( )图形 的位置关系,必须涉及 ( )图形;(2)只有( )对称轴.
如果把轴对称图形沿对称轴 分成两部分,那么这两个图形 就关于这条直线成轴对称.
如果把两个成轴对称的图形 拼在一起看成一个整体,那么它就是一个轴对称图形.
①关于某直线对称的两个图形是全等形。 ②如果两个图形关于某条直线对称，那么对称轴是 任何一对对应点所连线段的垂直平分线。 ③轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。 ④如果两个图形的对应点连线被同条直线垂直平分，那么这两个图形关于这条直线对称。
练习：1、国旗是一个国家的象征，观察下面的国旗，是轴对称图形的是（ ）A.加拿大、韩国、乌拉圭 B.加拿大、瑞典、澳大利亚C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士
加拿大 韩国 澳大利亚 乌拉圭 瑞典 瑞士
2、小明照镜子的时候，发现T恤上的英文单词在镜子中呈现“ ”的样子，请你判断这个英文单词是（ ）
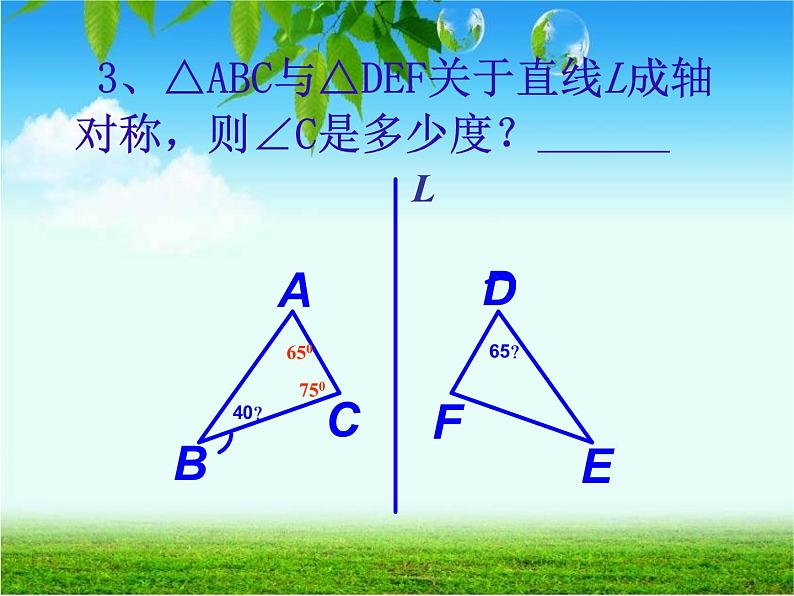
3、△ABC与△DEF关于直线L成轴对称，则∠C是多少度？
1、什么叫线段垂直平分线？
经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫中垂线。
2、线段垂直平分线有什么性质？
线段垂直平分线上的点与这条线段的两个端点的距离相等 （纯粹性）。
3.逆定理：与一条线段两个端点距离相等的点，在线段的垂直平分线上。（完备性）
4.线段垂直平分线的集合定义：
线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合。
三.用坐标表示轴对称小结： 在平面直角坐标系中，关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
点（x, y）关于x轴对称的点的坐标为______.点（x, y）关于y轴对称的点的坐标为______.
2、已知点P(2a+b,-3a)与点P’(8,b+2).若点p与点p’关于x轴对称，则a=_____ b=_______.若点p与点p’关于y轴对称，则a=_____ b=_______.
例：已知△ABC的三个顶点的坐标分别为A (-3，5),B(- 4，1),C(-1，3)，作出△ABC关于y轴对称的图形。
解：点A(-3,5),B(-4,1),C(-1,3)，关于y轴对称点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
归纳:（P44）先求出已知图形中的 特殊点(如多边形的顶点或端点)的对应点的坐标,描出并连接这些点,就可 得到这个图形的轴对称图形.
思考：如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗?
点（x, y）关于直线x=1对称的点的坐标为（2-x, y）
如图，分别作出△ABC关于直线x=1（记为m) 和直线y=-1（记为n）对称的图形，它们的对应点的坐标之间分别有什么关系？
点（x, y）关于直线x=1对称的点的坐标为（2-x, y）关于直线y=-1对称的点的坐标为（x, -2-y）点（x, y）关于直线x=m对称的点的坐标为（2m-x, y）,关于直线y=n对称的点的坐标为（x, 2n-y）
类似: 若两点(x1，y1)、(x2，y2)关于 直线y=n对称，则 ;
归纳:若两点(x1，y1)、(x2，y2)关于 直线x=m对称，则;
(m= )
(n= )
1.如图，△ABC中，边AB、BC的垂直平分线交于点P。（1）求证：PA=PB=PC。（2）点P是否也在边AC的垂直平分线上呢？由此你能得出什么结论？
结论：三角形三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等。
4.利用轴对称变换作图：
如图：要在燃气管道L上修建一个泵站，分别向A、B两镇供气，泵站修在管道什么地方，可使所用的输气管道线最短？
1.有A、B、C三个村庄，现准备要建一所学校，要求学校到三个村庄的距离相等，请你确定学校的位置。
1. 如图，A.B两地在一条河的两岸，现要在河上建一座桥MN，桥造在何处才能使从A到B的路径AMNB最短？（假设河的两岸是平行的直线，桥要与河垂直）
作法：1.将点B沿垂直与河岸的方向平移一个河宽到E， 2.连接AE交河对岸与点M, 则点M为建桥的位置，MN为所建的桥。证明：由平移的性质，得 BN∥EM 且BN=EM, MN=CD, BD∥CE, BD=CE,所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN,若桥的位置建在CD处，连接,则AB两地的距离为：AC+CD+DB=AC+CD+CE=AC+CE+MN,在△ACE中，∵AC+CE＞AE, ∴AC+CE+MN＞AE+MN,即AC+CD+DB ＞AM+MN+BN所以桥的位置建在CD处，AB两地的路程最短。
2. 如图，A、B是两个蓄水池，都在河流a的同侧，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A、B两地，问该站建在河边什么地方，可使所修的渠道最短，试在图中确定该点，作法：作点B关于直线 a 的对称点点C,连接AC交直线a于点D，则点D为建抽水站的位置。证明：在直线 a 上另外任取一点E，连接,∵点B.C关于直线 a 对称,点D.E在直线 a上，∴DB=DC,EB=EC,∴AD+DB=AD+DC=AC, AE+EB=AE+EC在△ACE中，AE+EC＞AC,即 AE+EC＞AD+DB 所以抽水站应建在河边的点D处，
某中学七（4）班举行文艺晚会，桌子摆成两直条(如图中的AO，BO)，AO桌面上摆满了桔子，OB桌面上摆满了糖果，坐在C处的学生小明先拿桔子再拿糖果，然后回到座位，请你帮助他设计一条行走路线，使其所走的总路程最短？　作法：1.作点C关于直线 OA 的 对称点点D, 2. 作点C关于直线 OB 的对称点点E, 3.连接DE分别交直线OA.OB于点M.N，则CM+MN+CN最短
　证明：在直线OA 上另外任取一点G，连接…∵点D,点C关于直线OA对称， 点G.H在OA上，∴DG=CG, DM=CM, 同理NC=NE，HC=HE,∴CM+CN+MN=DM+EN+MN=DE,CG+GH+HC=DG+GH+HE,∵DG+GH+HE＞DE（两点之间，线段最短），即CG+GH+HC＞CM+CN+MN 即CM+CN+MN最短
4. 如图：C为马厩，D为帐篷，牧马人某一天要从马厩牵出马，先到草地边某一处牧马，再到河边饮马，然后回到帐篷，请你帮他确定这一天的最短路线，作法：1.作点C关于直线 OA 的 对称点点F, 2. 作点D关于直线 OB 的对称点点E, 3.连接EF分别交直线OA.OB于点G.H，则CG+GH+DH最短
证明：在直线OA 上另外任取一点G，连接…∵点F,点C关于直线OA对称，点G.M在OA上，∴GF=GC,FM=CM, 同理HD=HE，ND=NE,∴CM+MN+ND=FM+MN+NE=FE,CG+GH+HD=FG+GH+HE,在四边形EFGH中，∵FG+GH+HE＞FE（两点之间，线段最短），即CG+GH+HD＞CM+MN+ND 即CM+MN+ND最短
4、如图，在等腰直角三角形ABC中，∠ACB=90°，点D为BC的中点，DE⊥AB，垂足为点E，过点B作BF∥AC交DE的延长线于点F，连接CF， （1）求证：AD ⊥CF （2）连接AF，试判断△ACF的形状，并说明理由。
5.如图，在Rt△ABC中，∠C=90，DE是AB的垂直平分线，连接AE，∠CAE：∠DAE=1：2，求∠B的度数。
6.如下图△ABC中，AC=16cm，DE为AB的垂直平分线， △BCE的周长为26cm，求BC的长。
7.如图：在△ABC中，DE是AC的垂直平分线，AC=5厘米，△ABD的周长等于13厘米，则△ABC的周长是 。
三.（等腰三角形)知识点回顾
1.等腰三角形的性质①.等腰三角形的两个底角相等，（简写成“等边对等角”）②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（简写成“三线合一”）2、等腰三角形的判定： 如果一个三角形有两个角相等，那么这两个角所对的边也相等。（简写成“等角对等边”）
四.（等边三角形)知识点回顾
1.等边三角形的性质： 等边三角形的三个角都相等，并且每一个角都等于600 。2、等边三角形的判定： ①三个角都相等的三角形是等边三角形。 ②有一个角是600的等腰三角形是等边三角形。3.在直角三角形中，如果一个锐角等于300，那么它所对的直角边等于斜边的一半。
1、如图，在△ABC中，AB=AC时，(1)∵AD⊥BC∴∠ ____= ∠_____;____=____(2) ∵AD是中线∴____⊥____; ∠_____= ∠_____(3) ∵ AD是角平分线∵____ ⊥____;_____=____
2、“有一个等腰三角形的两条边长分别是4cm和8cm，则周长为
3、若等腰三角形的一个角为400，则另外两个角的度数为
700,700 或 400，1000
4、已知，如图: AB=AC AD=DC=BC 则∠A=
5、已知，如图AB=AB=CD AD=BD 则∠BAC=
1、哪个在镜子中的像跟原来的一样？(直线表示进镜子、垂直放置在纸条前)
口 木 E 目 人 晶 S N 中 田
★ ★ ★ ★ ★ ★ ★
6、如图，在△ABC中，AB=AC=16cm，AB的垂直平分线交AC于D，如果BC=10cm，那么△BCD的周长是_______cm.
7、如图，P、Q是△ABC边上的两点，BP=PQ=QC=AP=AQ，求∠BAC的度数。
6、等腰三角形的一个角为100°，底角为_____
7、等腰三角形的周长为16cm，腰比底长2cm，则腰长为_______
8、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
9、如下图△ABC中，AC=16cm，DE为AB的垂直平分线， △BCE的周长为26cm，求BC的长。