北师大版八年级上册1 平均数教课内容课件ppt

这是一份北师大版八年级上册1 平均数教课内容课件ppt，共19页。

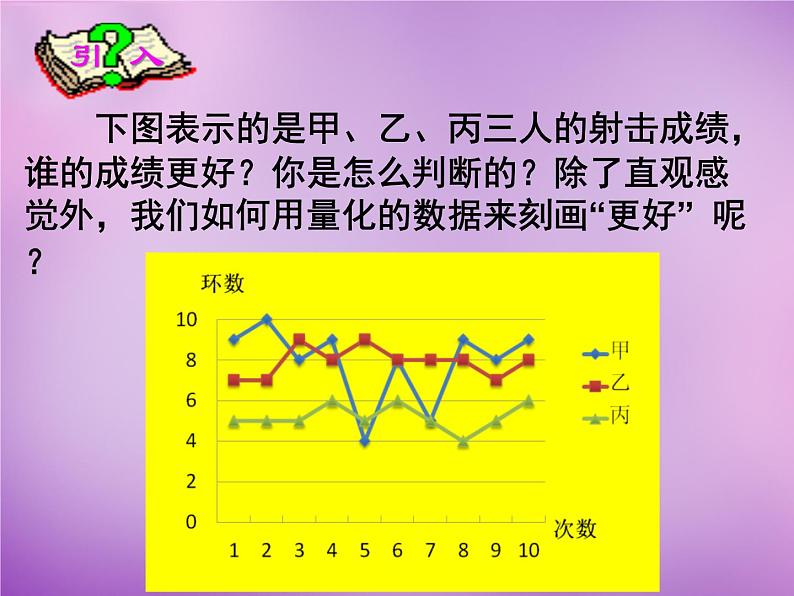
下图表示的是甲、乙、丙三人的射击成绩，谁的成绩更好？你是怎么判断的？除了直观感觉外，我们如何用量化的数据来刻画“更好” 呢？
数学上，我们常借助平均数、中位数、众数、方差等来对数据进行分析和刻画.
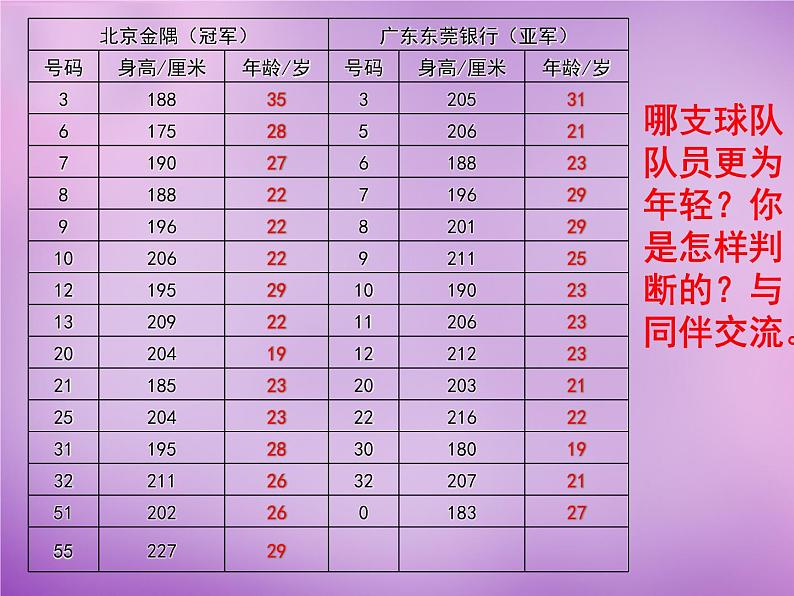
哪支球队队员更为年轻？你是怎样判断的？与同伴交流。
　　已知一组数据x1，x2，x3，x4的平均数是3，则3x1+3，x2+3，x3+3，x4+3的平均数为（ ）。
　　已知一组数据x1，x2，x3的平均数是a，则2x1-1,2x2-1，2x3-1的平均数为 (　　)
（1） 如果根据三项测试的平均成绩决定录用人选，那么谁将被录用？
例1 某广告公司欲招聘广告策划人员一名，对A ，B，C 三名候选人进行了三项素质测试，他们的各项测试成绩如下表所示：
解:(1)A的平均成绩为(72+50+88)÷3=70(分) B的平均成绩为(85+74+45)÷3=68(分) C的平均成绩为(67+70+67)÷3=68(分) 因此候选人 A 将被录用。
（2）根据实际需要，公司将创新、综合知识和语言三项测试得分按 4∶3∶1 的比例确定各人的测试成绩，此时谁将被录用？
(2)根据题意，三人的测试成绩如下： A的测试成绩为(72×4+50×3+88×1) ÷(4+3+1)=65.75(分) B的测试成绩为(85×4+74×3+45×1) ÷ (4+3+1)=75.875(分) C的测试成绩为(67×4+70×3+67×1) ÷(4+3+1)=68.125(分) 因此候选人B 将被录用。
（1）（2）的结果不一样说明了什么?
在实际问题中，一组数据里的各个数据的“重要程度” 未必相同。因而，在计算这组数据的平均数时，往往给每个数据一个“权 ”。
加权平均数的计算方法：各数据与权的积的和，除以权的和。
算术平均数是加权平均数各项的权都相等 的一种特殊情况，即算术平均数是一种特殊的加权平均数,而加权平均数不一定是算术平均数。
算术平均数与加权平均数的关系
1.小明骑自行车的速度是15千米/时， 步行的速度是5千米/时。(1)如果小明先骑自行车1小时，然后又步行了1小时，那么他的平均速度是多少？(2)如果小明先骑自行车2小时，然后步行了3小时，那么他的平均速度是多少？
解：小颖这学期的体育成绩是（92×20%+80×30%+84×50%） ÷（20%+30%+ 50% ） = 84.4（分）答：小颖这学期的体育成绩是84.4分。
2.某校规定学生的体育成绩由三部分组成：早锻炼及体育课外活动占成绩的20%，体育理论测试占30%，体育技能测试占50%。小颖的上述三项成绩依次为 92分、80 分、84 分，则小颖这学期的体育成绩是多少分？
（1）若将服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%，20%，30%，40%的比例计算各班的广播操比赛成绩，那么哪个班的成绩最高？（2）你认为上述四项中，哪一项更为重要？请你按自己的想法设计一个评分方案。根据你的评分方案，哪一个班的广播操比赛成绩最高？与同伴进行交流。
某学校进行广播操比赛，比赛打分包括以下几 项：服装统一、进退场有序、动作规范、动作整齐 (每项满分10分),其中三个班级的成绩分别如下：
解:(1)一班的广播操成绩为： （9×10%＋8×20%＋9×30%＋8×40%） ÷ （10%+20%+30%+40%）=8.4(分) 二班的广播操成绩为： （10×10%＋9×20%＋7×30%＋8×40% ）÷ （10%+20%+30%+40%） =8.1(分) 三班的广播操成绩为： （8×10%＋9×20%＋8×30%＋9×40% ）÷ （10%+20%+30%+40%） =8.6(分) 因此，三班的广播操成绩最高。(2) 权有差异，得出的结果就会不同，也就是说 权的差异对结果有影响。
本节课“我知道了…”， “我发现了…”， “我学会了…”， “我想我以后将…”