福建省泉州市石狮市2020-2021学年七年级上学期期末数学试卷（word版 含答案）

这是一份福建省泉州市石狮市2020-2021学年七年级上学期期末数学试卷（word版 含答案），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年福建省泉州市石狮市七年级（上）期末数学试卷
(附参考答案与试题解析)

一、选择题（本题共10小题，每小题4分，共40分）
1．（4分）﹣的倒数是（　　）
A． B．﹣3 C．3 D．﹣
2．（4分）据相关报道，开展精准扶贫工作五年以来，我国约有56000000人摆脱贫困，将数据56000000用科学记数法表示是（　　）
A．5.6×106 B．0.56×108 C．5.6×107 D．56×106
3．（4分）与﹣a2b3是同类项的是（　　）
A． B．﹣a3b2 C．2ab3 D．﹣2b3a2
4．（4分）“a，b两数的平方和”用代数式表示为（　　）
A．a2+b2 B．（a+b）2 C．a+b2 D．a2+b
5．（4分）若∠α＝55°，则∠α的余角是（　　）
A．35° B．45° C．135° D．145°
6．（4分）下列图形都是由六个相同的正方形组成的，经过折叠不能围成正方体的是（　　）
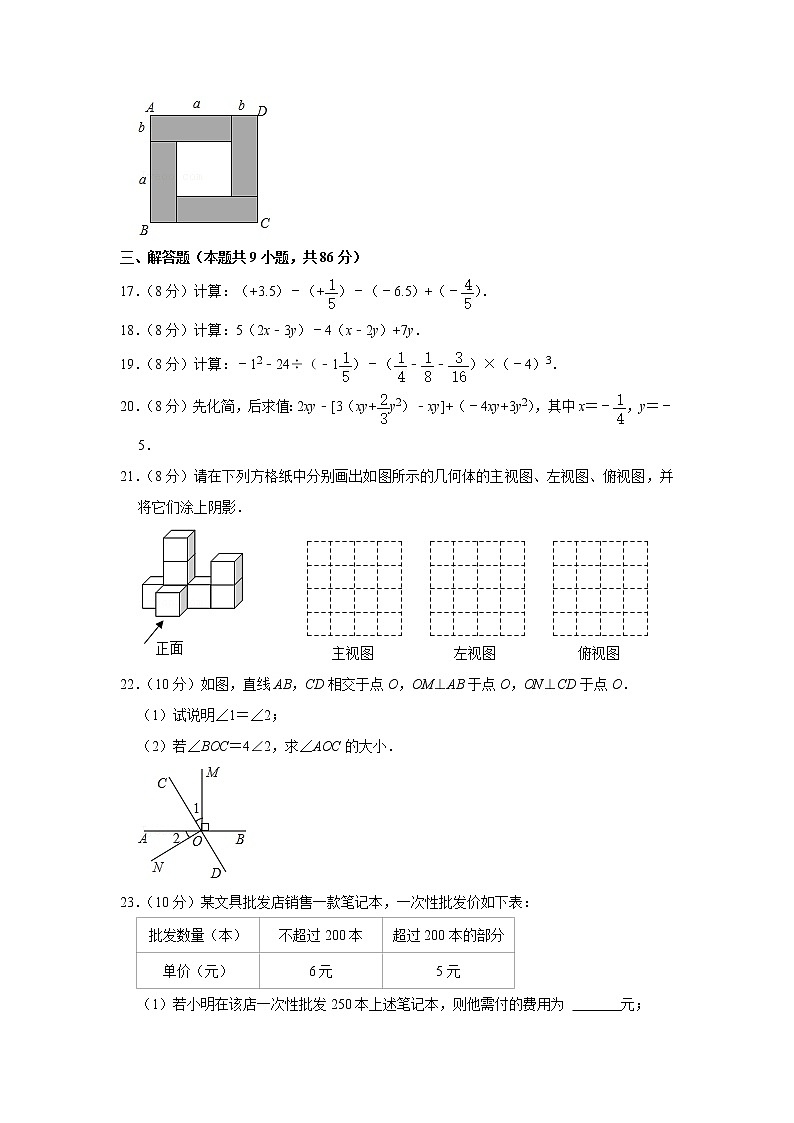
A． B．
C． D．
7．（4分）在一次植树活动中，小明说“只要定出两棵树的位置，就能确定同一行树所在的直线”，其数学依据是（　　）
A．两点之间，线段最短
B．垂线段最短
C．两点确定一条直线
D．过直线外一点有且只有一条直线与这条直线平行
8．（4分）已知代数式M＝2x2﹣7x﹣1，N＝x2﹣7x﹣2，则无论x取何值，它们的大小关系是（　　）
A．M＝N
B．M＞N
C．M＜N
D．M，N的大小关系与x的取值有关
9．（4分）已知多项式﹣7ambn+5ab2﹣1（m，n为正整数）是按a的降幂排列的四次三项式，则（﹣n）m的值为（　　）
A．﹣1 B．3或﹣4 C．﹣1或4 D．﹣3或4
10．（4分）已知∠α的两边分别平行于∠β的两边．若∠α＝60°，则∠β的大小为（　　）
A．30° B．60° C．30°或60° D．60°或120°
二、填空题（本题共6小题，每小题4分，共24分）
11．（4分）﹣|﹣2|＝　 　．
12．（4分）比较大小：　 　（填“＞”或“＜”）
13．（4分）如图，已知线段AB＝10cm，点C为线段AB上的一点，点D，E分别为线段AC，BC的中点．若CD＝2cm，则线段AE的长为 　 　cm．

14．（4分）如图，AB∥CD，∠EGB＝50°，则∠CHG的大小为 　 　．

15．（4分）已知代数式x2﹣2x+1的值为2，则代数式2020x2﹣4040x+1的值为 　 　．
16．（4分）如图，正方形ABCD是由四个长都为a，宽都为b（a＞b）的小长方形拼接围成的．已知每个小长方形的周长为18，面积为，我们可以通过计算正方形ABCD面积的方法求出代数式a﹣b的值，则这个值为 　 　．

三、解答题（本题共9小题，共86分）
17．（8分）计算：（+3.5）﹣（+）﹣（﹣6.5）+（﹣）．
18．（8分）计算：5（2x﹣3y）﹣4（x﹣2y）+7y．
19．（8分）计算：﹣12﹣24÷（﹣1）﹣（﹣﹣）×（﹣4）3．
20．（8分）先化简，后求值：2xy﹣[3（xy+y2）﹣xy]+（﹣4xy+3y2），其中x＝﹣，y＝﹣5．
21．（8分）请在下列方格纸中分别画出如图所示的几何体的主视图、左视图、俯视图，并将它们涂上阴影．

22．（10分）如图，直线AB，CD相交于点O，OM⊥AB于点O，ON⊥CD于点O．
（1）试说明∠1＝∠2；
（2）若∠BOC＝4∠2，求∠AOC的大小．

23．（10分）某文具批发店销售一款笔记本，一次性批发价如下表：
批发数量（本）
不超过200本
超过200本的部分
单价（元）
6元
5元
（1）若小明在该店一次性批发250本上述笔记本，则他需付的费用为 　 　元；
（2）某零售店店主小强分两次向该批发店共批发1200本该款笔记本，第一次批发m本，且第二次批发的数量超过第一次批发的数量，则小强两次批发笔记本共付费多少元？（用含m的代数式表示）
24．（13分）如图，将一块直角三角板ABC按如图所示放置，点A，B在数轴上，AB＝5，点B在点A右边，点A表示的数是﹣3．
（1）直接填空：点B表示的数是 　 　；
（2）将三角板ABC沿数轴正方向移动至三角板A'B'C'的位置，点A，B，C的对应点分别是点A'，B'，C'．
①连结CA'，若CA'恰好将三角板ABC的面积分成2：3的两部分，求这时点A'表示的数；
②设三角板ABC的移动速度为每秒2个单位长度，点E为线段AA'的中点，点F在线段BB'上，且BB'＝4BF．设三角板ABC移动的时间为t（秒）．试探索：是否存在某一时刻t，使点E与点F表示的两个数互为相反数？若存在，试求出t的值；若不存在，请说明理由．

25．（13分）已知AB∥CD，点E是AB，CD之间的一点．
（1）如图1，试探索∠AEC，∠BAE，∠DCE之间的数量关系；
以下是小明同学的探索过程，请你结合图形仔细阅读，并完成填空（理由或数学式）：
解：过点E作PE∥AB（过直线外一点有且只有一条直线与这条直线平行）．
∵AB∥CD（已知），
∴PE∥CD（ 　 　），
∴∠BAE＝∠1，∠DCE＝∠2（ 　 　），
∴∠BAE+∠DCE＝　 　+　 　（等式的性质）．
即∠AEC，∠BAE，∠DCE之间的数量关系是 　 　．
（2）如图2，点F是AB，CD之间的一点，AF平分∠BAE，CF平分∠DCE．
①若∠AEC＝74°，求∠AFC的大小；
②若CG⊥AF，垂足为点G，CE平分∠DCG，∠AEC+∠AFC＝126°，求∠BAE的大小．



2020-2021学年福建省泉州市石狮市七年级（上）期末数学试卷
参考答案与试题解析
一、选择题（本题共10小题，每小题4分，共40分）
1．（4分）﹣的倒数是（　　）
A． B．﹣3 C．3 D．﹣
【分析】依据倒数的定义解答即可．
【解答】解：﹣的倒数是﹣3．
故选：B．
2．（4分）据相关报道，开展精准扶贫工作五年以来，我国约有56000000人摆脱贫困，将数据56000000用科学记数法表示是（　　）
A．5.6×106 B．0.56×108 C．5.6×107 D．56×106
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值小于1时，n是负整数．
【解答】解：56000000＝5.6×107，
故选：C．
3．（4分）与﹣a2b3是同类项的是（　　）
A． B．﹣a3b2 C．2ab3 D．﹣2b3a2
【分析】所含字母相同，并且相同字母的指数也相同，这样的项叫做同类项．据此判断即可．
【解答】解：A、字母a、b的次数不相同，不是同类项，故本选项不符合题意；
B、字母a、b的次数不相同，不是同类项，故本选项不符合题意；
C、字母a的次数不相同，不是同类项，故本选项不符合题意；
D、有相同的字母，相同字母的指数也相同，是同类项，故本选项符合题意；
故选：D．
4．（4分）“a，b两数的平方和”用代数式表示为（　　）
A．a2+b2 B．（a+b）2 C．a+b2 D．a2+b
【分析】“a，b两数的平方和”是先平方再相加．
【解答】解：“a，b两数的平方和”代数式表示为用a2+b2．故选A．
5．（4分）若∠α＝55°，则∠α的余角是（　　）
A．35° B．45° C．135° D．145°
【分析】由余角定义得∠α的余角为90°减去55°即可．
【解答】解：由余角定义得∠α的余角等于90°﹣55°＝35°．
故选：A．
6．（4分）下列图形都是由六个相同的正方形组成的，经过折叠不能围成正方体的是（　　）
A． B．
C． D．
【分析】根据正方体展开图的特征，逐一判断即可．
【解答】解：A．经过折叠能围成正方体，故正确；
B．经过折叠能围成正方体，故正确；
C．经过折叠后，有两个面重叠，不能围成正方体，故错误；
D．经过折叠能围成正方体，故正确；
故选：C．
7．（4分）在一次植树活动中，小明说“只要定出两棵树的位置，就能确定同一行树所在的直线”，其数学依据是（　　）
A．两点之间，线段最短
B．垂线段最短
C．两点确定一条直线
D．过直线外一点有且只有一条直线与这条直线平行
【分析】两棵树的位置相当于两个点，要确定同一行树所在的直线，即两点确定一条直线．
【解答】解：由题意得：
两点确定一条直线，
故选：C．
8．（4分）已知代数式M＝2x2﹣7x﹣1，N＝x2﹣7x﹣2，则无论x取何值，它们的大小关系是（　　）
A．M＝N
B．M＞N
C．M＜N
D．M，N的大小关系与x的取值有关
【分析】用作差法比较大小．
【解答】解：M﹣N＝（2x2﹣7x﹣1）﹣（x2﹣7x﹣2）
＝2x2﹣7x﹣1﹣x2+7x+2
＝x2+1，
∵x2≥0，
∴x2+1＞0，
∴M＞N，
故选：B．
9．（4分）已知多项式﹣7ambn+5ab2﹣1（m，n为正整数）是按a的降幂排列的四次三项式，则（﹣n）m的值为（　　）
A．﹣1 B．3或﹣4 C．﹣1或4 D．﹣3或4
【分析】根据多项式及降幂排列的定义可得m＞1，m+n＝4，即可求解m，n的值，再分别代入计算可求解．
【解答】解：由题意得：m＞1，m+n＝4，
∴m＝2，n＝2或m＝3，n＝1，
当m＝2，n＝2时，（﹣n）m＝（﹣2）2＝4；
当m＝3，n＝1时，（﹣n）m＝（﹣1）3＝﹣1．
故选：C．
10．（4分）已知∠α的两边分别平行于∠β的两边．若∠α＝60°，则∠β的大小为（　　）
A．30° B．60° C．30°或60° D．60°或120°
【分析】根据题意画图如图（1），根据平行线性质两直线平行，同位角相等，即可得出∠α＝∠1＝∠β，即可得出答案，如图（2）根据平行线性质，两直线平行，同旁内角互补，∠α+∠2＝180°，再根据两直线平行，内错角相等，∠2＝∠β，即可得出答案．
【解答】解：如图1，
∵a∥b，
∴∠1＝∠α，
∵c∥d，
∴∠β＝∠1＝∠α＝60°；
如图（2），
∵a∥b，
∴∠α+∠2＝180°，
∵c∥d，
∴∠2＝∠β，
∴∠β+∠α＝180°，
∵∠α＝60°，
∴∠β＝120°．
综上，∠β＝60°或120°．
故选：D．


二、填空题（本题共6小题，每小题4分，共24分）
11．（4分）﹣|﹣2|＝　﹣2　．
【分析】计算绝对值要根据绝对值的定义求解|﹣2|，然后根据相反数的性质得出结果．
【解答】解：﹣|﹣2|表示﹣2的绝对值的相反数，|﹣2|＝2，所以﹣|﹣2|＝﹣2．
12．（4分）比较大小：　＞　（填“＞”或“＜”）
【分析】先把各数化为小数的形式，再根据负数比较大小的法则进行比较即可．
【解答】解：∵﹣＝﹣0.75＜0，﹣＝﹣0.8＜0，
∵|﹣0.75|＝0.75，|﹣0.8|＝0.8，0.75＜0.8，
∴﹣0.75＞﹣0.8，
∴﹣＞﹣．
故答案为：＞．
13．（4分）如图，已知线段AB＝10cm，点C为线段AB上的一点，点D，E分别为线段AC，BC的中点．若CD＝2cm，则线段AE的长为 　7　cm．

【分析】根据线段中点的性质，可得DC、EC的长，根据线段的和差，可得DE的长．
【解答】解：由点D是线段AC的中点，点E是线段BC的中点，得
AD＝DC＝AC，CE＝BC．
∵CD＝2cm，
∴AD＝2cm，
由线段的和差，得
DE＝DC+CE＝AC+BC＝（AC+BC）＝AB＝×10＝5cm，
∴AE＝AD+DE＝2+5＝7cm，
故答案为：7cm．
14．（4分）如图，AB∥CD，∠EGB＝50°，则∠CHG的大小为 　130°　．

【分析】根据平行线的性质可得∠EHD＝∠EGB＝50°，再利用邻补角的性质可求解．
【解答】解：∵AB∥CD，∠EGB＝50°，
∴∠EHD＝∠EGB＝50°，
∴∠CHG＝180°﹣∠EHD＝130°．
故答案为：130°．
15．（4分）已知代数式x2﹣2x+1的值为2，则代数式2020x2﹣4040x+1的值为 　2021　．
【分析】由已知代数式的值求出x2﹣2x的值，原式变形后代入计算即可求出值．
【解答】解：∵x2﹣2x+1＝2，
∴x2﹣2x＝1，
则原式＝2020（x2﹣2x）+1＝2020+1＝2021．
故答案为：2021．
16．（4分）如图，正方形ABCD是由四个长都为a，宽都为b（a＞b）的小长方形拼接围成的．已知每个小长方形的周长为18，面积为，我们可以通过计算正方形ABCD面积的方法求出代数式a﹣b的值，则这个值为 　6　．

【分析】用大正方形的面积减去4个长方形的面积，然后进行计算即可．
【解答】解：由题意得：2（a+b）＝18，ab＝，
∴a+b＝9，
∴（a﹣b）2
＝（a+b）2﹣4ab
＝81﹣45
＝36，
又∵a＞b，
∴a﹣b＝6，
故答案为：6．
三、解答题（本题共9小题，共86分）
17．（8分）计算：（+3.5）﹣（+）﹣（﹣6.5）+（﹣）．
【分析】先将有理数的加减混合运算统一成加法，再运用加法的交换律、加法的结合律进行计算．
【解答】解：（+3.5）﹣（+）﹣（﹣6.5）+（﹣）
＝
＝（3.5+6.5）﹣（+）
＝10﹣1
＝9．
18．（8分）计算：5（2x﹣3y）﹣4（x﹣2y）+7y．
【分析】原式去括号，合并同类项进行化简．
【解答】解：原式＝10x﹣15y﹣4x+8y+7y
＝6x．
19．（8分）计算：﹣12﹣24÷（﹣1）﹣（﹣﹣）×（﹣4）3．
【分析】先算乘方和括号内的式子，然后计算括号外的乘除法、最后算加减法即可．
【解答】解：﹣12﹣24÷（﹣1）﹣（﹣﹣）×（﹣4）3
＝﹣1﹣24÷（﹣）﹣（﹣﹣）×（﹣64）
＝﹣1+24×﹣×（﹣64）+×（﹣64）+×（﹣64）
＝﹣1+20+16+（﹣8）+（﹣12）
＝15．
20．（8分）先化简，后求值：2xy﹣[3（xy+y2）﹣xy]+（﹣4xy+3y2），其中x＝﹣，y＝﹣5．
【分析】先根据整式的运算法则进行化简，然后将x与y的值代入原式即可求出答案．
【解答】解：原式＝2xy﹣（3xy+2y2﹣xy）+（﹣4xy+3y2）
＝2xy﹣3xy﹣2y2+xy﹣4xy+3y2
＝﹣4xy+y2．
当，y＝﹣5时，
原式＝．
21．（8分）请在下列方格纸中分别画出如图所示的几何体的主视图、左视图、俯视图，并将它们涂上阴影．

【分析】根据题意分别作出主视图、左视图、俯视图，涂上阴影即可．
【解答】解：作图如下：

22．（10分）如图，直线AB，CD相交于点O，OM⊥AB于点O，ON⊥CD于点O．
（1）试说明∠1＝∠2；
（2）若∠BOC＝4∠2，求∠AOC的大小．

【分析】（1）利用同角的余角相等解答即可得出结论；
（2）利用（1）的结论，等量代换可得∠BOC＝4∠1，利用∠BOM＝90°＝3∠1，求得∠1的度数，则∠AOC＝90°﹣∠1．
【解答】解：（1）∵OM⊥AB，ON⊥CD，
∴∠AOC+∠1＝90°，∠AOC+∠2＝90°，
∴∠1＝∠2．
（2）∵OM⊥AB，
∴∠BOM＝90°．
∵∠1＝∠2，∠BOC＝4∠2，
∴∠BOC＝4∠1．
∴∠BOM＝∠BOC﹣∠1＝4∠1﹣∠1＝3∠1，
即3∠1＝90°，
∴∠1＝30°．
∴∠AOC＝∠CON﹣∠1＝90°﹣30°＝60°．
23．（10分）某文具批发店销售一款笔记本，一次性批发价如下表：
批发数量（本）
不超过200本
超过200本的部分
单价（元）
6元
5元
（1）若小明在该店一次性批发250本上述笔记本，则他需付的费用为 　1450　元；
（2）某零售店店主小强分两次向该批发店共批发1200本该款笔记本，第一次批发m本，且第二次批发的数量超过第一次批发的数量，则小强两次批发笔记本共付费多少元？（用含m的代数式表示）
【分析】（1）根据题意，总费用＝200本的费用+50本的费用，可得答案；
（2）根据第二次批发的数量超过第一次批发的数量，可知1200﹣m＞m，则m＜600，分两种情况分别计算：①当0＜m≤200时，1200﹣m≥1000，②当200＜m＜600时，600＜1200﹣m＜1000．
【解答】解：（1）200×6+5（250﹣200）＝1450，
答：他需付的费用为1450元；
故答案为：1450；
（2）由题意得：1200﹣m＞m，
∴m＜600，
①当0＜m≤200时，1200﹣m≥1000，
依题意，得
小强两次批发笔记本共付费为：6m+[200×6+5（1200﹣m﹣200）]＝6m+1200+5000﹣5m＝m+6200．
②当200＜m＜600时，600＜1200﹣m＜1000，依题意，得
小强两次批发笔记本共付费为：[200×6+5（m﹣200）]+[200×6+5（1200﹣m﹣200）]＝1200+5m﹣1000+1200+5000﹣5m＝6400．
综上所述，当0＜m≤200时，小强两次批发笔记本共付费（m+6200）元；
当200＜m＜600时，小强两次批发笔记本共付费6400元．
24．（13分）如图，将一块直角三角板ABC按如图所示放置，点A，B在数轴上，AB＝5，点B在点A右边，点A表示的数是﹣3．
（1）直接填空：点B表示的数是 　2　；
（2）将三角板ABC沿数轴正方向移动至三角板A'B'C'的位置，点A，B，C的对应点分别是点A'，B'，C'．
①连结CA'，若CA'恰好将三角板ABC的面积分成2：3的两部分，求这时点A'表示的数；
②设三角板ABC的移动速度为每秒2个单位长度，点E为线段AA'的中点，点F在线段BB'上，且BB'＝4BF．设三角板ABC移动的时间为t（秒）．试探索：是否存在某一时刻t，使点E与点F表示的两个数互为相反数？若存在，试求出t的值；若不存在，请说明理由．

【分析】（1）设数轴的原点为O，利用已知条件求得线段OB即可得出结论；
（2）利用高相等的三角形的面积比等于底的比可得AA'：A'B＝2：3或AA'：A'B＝3：2，根据AB＝A′B′＝5可求AA'＝2，A'B＝3或AA'＝3，A'B＝2，结合数轴即可得出结论；
（3）存在某一时刻t，使点E与点F表示的两个数互为相反数．依据题意画出图形，用t的代数式表示出点F，E对应的数字，利用点E与点F表示的两个数互为相反数列出方程，解方程即可求得结论．
【解答】解：（1）设数轴的原点为O，如图，

∵点A表示的数是﹣3，
∴OA＝3．
∵AB＝5，
∴OB＝AB﹣OA＝5﹣3＝2．
∴点B表示的数是：2．
故答案为：2．
（2）①如图1，

∵CA'恰好将三角板ABC的面积分成2：3的两部分，
∴AA'：A'B＝2：3或AA'：A'B＝3：2．
∵AB＝5，
∴AA'＝2，A'B＝3或AA'＝3，A'B＝2．
∵点A表示的数是﹣3，
∴点A'表示的数是﹣1或0．
②存在某一时刻t，使点E与点F表示的两个数互为相反数．如图2，

AA'＝BB'＝2t．
∵点E为AA'的中点，
∴，
∴点E表示的数是﹣3+t．
∵BB'＝4BF，
∴．
∴点F表示的数是．
∵点E表示的数与点F表示的数是互为相反数，
∴，
解得 ．
即当时，点E与点F表示的两个数互为相反数．
25．（13分）已知AB∥CD，点E是AB，CD之间的一点．
（1）如图1，试探索∠AEC，∠BAE，∠DCE之间的数量关系；
以下是小明同学的探索过程，请你结合图形仔细阅读，并完成填空（理由或数学式）：
解：过点E作PE∥AB（过直线外一点有且只有一条直线与这条直线平行）．
∵AB∥CD（已知），
∴PE∥CD（ 　平行于同一条直线的两条直线平行　），
∴∠BAE＝∠1，∠DCE＝∠2（ 　两直线平行，内错角相等　），
∴∠BAE+∠DCE＝　∠1　+　∠2　（等式的性质）．
即∠AEC，∠BAE，∠DCE之间的数量关系是 　∠AEC＝∠BAE+∠DCE　．
（2）如图2，点F是AB，CD之间的一点，AF平分∠BAE，CF平分∠DCE．
①若∠AEC＝74°，求∠AFC的大小；
②若CG⊥AF，垂足为点G，CE平分∠DCG，∠AEC+∠AFC＝126°，求∠BAE的大小．


【分析】（1）结合图形利用平行线的性质填空即可；
（2）①利用图1的结论来解决即可；
②利用①的结论先求∠AEC，∠AFC的度数，然后再利用图1的结论解答即可．
【解答】解：（1）平行于同一条直线的两条直线平行，
两直线平行，内错角相等，
∠1，∠2，
∠AEC＝∠BAE+∠DCE，
故答案为：平行于同一条直线的两条直线平行，
两直线平行，内错角相等，
∠1，∠2，
∠AEC＝∠BAE+∠DCE，
（2）①由（1）得：
∠AEC＝∠BAE+∠DCE，
∠AFC＝∠BAF+∠DCF，
∵AF平分∠BAE，CF平分∠DCE，
∴∠BAF＝∠BAE，∠DCF＝∠DCE，
∴∠AFC＝∠BAF+∠DCF
＝∠BAE+∠DCE
＝∠AEC
＝×74°
＝37°；
②由①得：∠AEC＝2∠AFC，
∵∠AEC+∠AFC＝126°，
∴∠AFC＝42°，∠AEC＝82°，
∵CG⊥AF，
∴∠CGF＝90°，
∴∠GCF＝48°，
∵CE平分∠DCG，
∴∠GCE＝∠ECD，
∵CF平分∠DCE，
∴∠DCE＝2∠DCF＝2∠ECF，
∴∠GCF＝3∠DCF，
∴∠DCF＝16°，
∴∠DCE＝32°，
∴∠BAE＝∠AEC﹣∠DCE＝52°．

声明：试题解析著作权属所有，未经书面同意，不得复制发布
日期：2021/12/31 5:11:42；用户：卫爸爸；邮箱：orFmNt5l7iMnhOwiAimBepsd0gQc@weixin.jyeoo.com；学号：41536311