人教版新课标A必修4第一章三角函数1.4 三角函数的图象与性质背景图ppt课件

展开

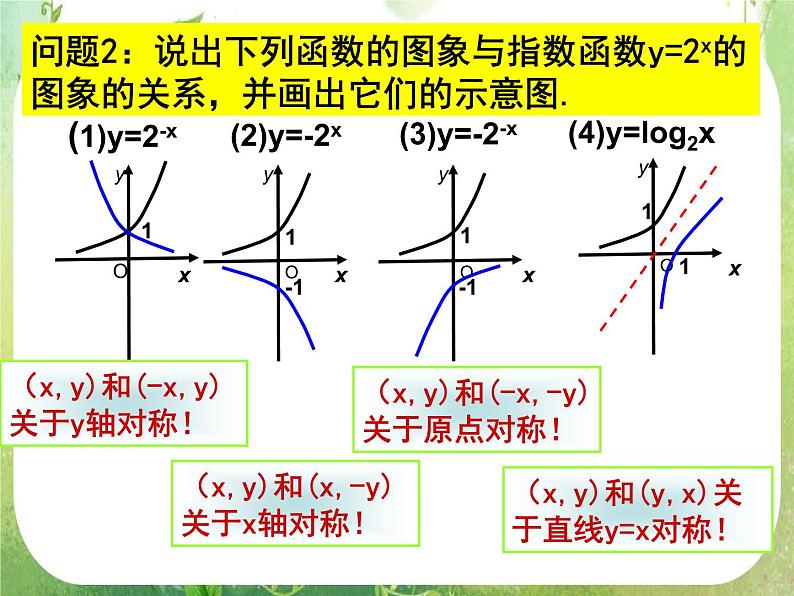
这是一份人教版新课标A必修4第一章三角函数1.4 三角函数的图象与性质背景图ppt课件

函数的图象要求:熟练掌握一次函数,二次函数,指数函数,对数函数,幂函数,反比例函数的图象.基本初等函数的图象作图函数图象的作法有两种常见的方法：一是描点法；二是图象变换法1.描点法：描点法作函数图象是根据函数解析式，列出函数中x,y的一些对应值表，在坐标系内描出点，最后用平滑的曲线将这些点连接起来.利用这种方法作图时，要与研究函数的性质结合起来 2.图象变换法：常用变换方法有四种，即平移变换、对称变换、翻折变换、伸缩变换。步骤：（1）确定定义域；（2）列表；（3）描点；（4）连线成图问题1：如何由f(x)=x2的图象得到下列各函数的图象？（1）f(x-1)=(x-1)2（2）f(x+1)=(x+1)2（3）f(x)+1=x2+1（4）f(x) -1=x2-1Oyxy=f(x-1)y=f(x+1)y=f(x)-1y=f(x)+111-1-1向左平移a个单位向右平移a个单位上移a下移ay=f（x）+ay=f（x）-ay=f(x)y=f(x-a)y=f(x+a)1、函数图象的平移变换：（设a>0)问题2：说出下列函数的图象与指数函数y=2x的图象的关系，并画出它们的示意图.(1)y=2-x(2)y=-2x(4)y=log2x(3)y=-2-xOyOyOyOy11-11-111（x,y)和(-x,y)关于y轴对称！（x,y)和(x,-y)关于x轴对称！（x,y)和(-x,-y)关于原点对称！（x,y)和(y,x)关于直线y=x对称！xxxx C1 :y=f(x) y=f(x) 关于y 轴对称关于x 轴对称C2 :y=f(-x) y=f(x)关于直线 x=a对称 y=f(x)关于直线 y = x对称关于原点对称2、对称变换：两个图象之间的对称C1:y=ax (0＜a≠1)C3 :y=-f(-x)C4 :y= -f(x)C6 : y=f(2a-x) C5:y=logax(0＜a≠1) y=f(x)关于点（a，0）对称y=-f(2a-x) 区别：一个函数图象自身的对称①偶函数的图象关于y轴对称；②奇函数的图象关于原点对称；③若函数f(x)满足：对于任意x∈R都有f(a+x)=f(a-x),则f(x)的图象关于直线x=a对称.问题3：分别在同一坐标系中作出下列各组函数的图象，并说明它们之间有什么关系？（1）y=2x与y=2|x|（2）y=log2x与y=|log2x|OxyOxy由y=f(x)的图象作y=f(|x|)的图象：由y=f(x)的图象作y=|f(x)|的图象：y=2x 保留y=f(x)中y轴右侧部分，再加上这部分关于y轴对称的图形. 保留y=f(x)中x轴上方部分，再加上下方部分关于x轴对称的图形.11y=2|x|y=log2xy=|log2x|3、翻折变换（含绝对值的函数的图象）（1）作函数f（| x |）的图象:①作出 f（x）当x≥0时的图象；②作①的关于y轴对称的图象.（2）作函数| f（x）|的图象：①作出 f（x）的图象；②把①的在x轴上方的图象保留不变，在x轴下方的图象关于x轴对称翻到x轴上方.（利用偶函数的性质）右留翻左上留下翻4.伸缩变换：y=f(x)y=f(wx)01，纵坐标伸长到原来的A倍y=f(x)y=Af(x)例1.将函数y=lgx的图象向左平移1个单位，再作关于原点对称的图形后.求所得图象对应的函数解析式.y=lgxy=lg(x+1)-y=lg(-x+1)y =-lg(-x+1)向左平移1个单位关于原点对称x换成-xy换成-yx 换成 x+1解：函数图象的应用题型1、图象变换练习. 说明由函数y=2x的图象经过怎样的图象变换可得到函数y=2-x-3+1的图象.解:(1)作出函数y=2x的图象关于y轴的对称图形，得y=2-x的图象；（2）把函数y=2-x的图象向左平移3个单位得到函数y=2-x-3的图象；（3）把函数y=2-x-3的图象向上平移1个单位得到函数y=2-x-3+1的图象. 分析:y=2x→y=2-x→y=2-x-3→y=2-x-3+1练习.y=lg(2x+6)的图象可看成是由y=lg(2x)的图象向平行移动个单位而得到. 2x→2x+6=2(x+3) x→x+3左3 y=lg(2x) →y=lg(2x+6)x的系数不为1，先提后移x换成x-1向下平移1个单位Oyx-11向右平移1个单位（1，-1）解：题型2、作图例3.已知函数y=|2x-2| （1）作出函数的图象；（2）指出函数的单调区间；（3）指出x取何值时，函数有最值。 Oxy3211-1y=2x y=2x-2 y=|2x-2| y=|2x-2|解：练习：分别画出下列函数的图象：(1)y＝2x＋2－1；(4)y＝x2－2|x|－1 (3)y＝sin|x|；(5)y＝|log2(x＋1)|.由图象可知f(x)的单调减区间为[0,1)和(1,+∞).xyo1.数形结合求参数的值或范围题型3、用图[小结] 有关方程实根个数问题，可以转化为函数图象交点问题.利用数形结合法进行求解.Oyx-414-1y=a(a=0)有两个交点y=a(04)有二个交点y=a(a<0)没有交点(3)关于x的方程|x2-4x+3|-a=x有三个不相等的实根，求实数a的值.（4）. 若直线y=2a与函数y=|ax-1|(0

相关课件更多