点和圆的位置关系PPT课件免费下载

人教版初中数学九年级上册课文《点和圆的位置关系》,完整版PPT课件免费下载，优秀PPT背景图搭配，精美的免费ppt模板。轻松备课，欢迎免费下载使用。

一、【知识回顾】

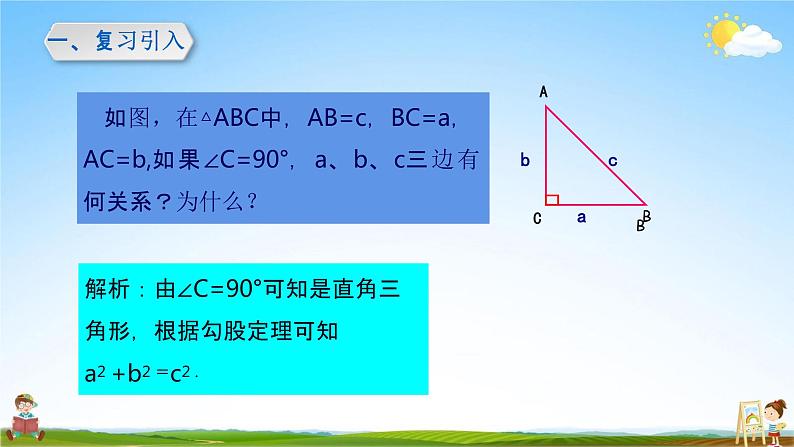
解析：由∠C=90°可知是直角三 角形，根据勾股定理可知a2 +b2 ＝c2 .如图，在△ABC中，AB=c，BC=a， AC=b,如果∠C=90°，a、b、c三边有 何关系？为什么？ACabcBB一、复习引入探究：假设a2 +b2 ＝c2，由勾股定理可知三角形ABC是直角三角 形，且∠C=90°，这与已知条件∠C≠90°矛盾。假设不成立，从 而说明原结论a2 +b2 ≠ c2 成立。ACB

二、【合作探究】

若将上面的条件改为“在△ABC中，AB=c，BC=a， 问结论a2 +b2 ≠ c2AC=b,∠C≠90°”，请 成立吗？请说明理由。

三、【课程主要内容】

这种证明方法与前面的证明方法不同，它是首先假设结论的反面 成立，然后经过正确的；逻辑推理得出与已知、定理、公理矛盾的 结论，从而得到原结论的正确。象这样的证明方法叫做反证法。发现知识：ABC则 （这与矛盾．假设不成立．∴ ．AB＝AC等角对等边 ）已知AB≠AC∠B ≠ ∠ C小结：反证法的步骤：假设结论的反面不成立→逻辑推理得出矛盾→肯定原结论正确。例１ 在△ABC中，AB≠AC,求证：∠B ≠ ∠ C 证明：假设_∠_B ＝ ∠_C_，三、应用新知A证明：假设a与b不平行，则可设它们相交于点A。那么过点A 就有两条直线a、b与直线c平行，这与“过直线 外一点有且只有一条直线与已知直线平行矛盾,假设不成立。∴a//b.已知：如图有a、b、c三条直线，且a//c,b//c.求证：a//ba b c例2小结：根据假设推出结论除了可以与已知条件矛盾以外， 还可以与我们学过的定理、公理矛盾例3 求证：在一个三角形中，至少有一个内角小于或等于60°。已知： △ ABC求证： △ ABC中至少有一个内角小于或等于60°.证明：假设。，．△ ABC中没有一个内角小于或等于60，°则 ∠A>60°,∠B>60°,∠C>60°∴ ∠A+∠B+∠C>60°+60°+60°=180°即 ∠A+∠B+∠C>180° 。这与 三角形的内角和为180度 矛盾．假设不成立．∴ △ ABC中至少有一个内角小于或等于60°.点拨：至少的反面是没有！

四、【随堂演练】

1、试说出下列命题的反面：（1）a是实数。 a不是实数 （2 )a大于2。（3）a小于2。 a大于或等于２ （4）至少有2个a小于或等于２ 没有两个（5）最多有一个 一个也没有 （6）两条直线平行。两直线相交

2、用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 假设a=b 。

3、用反证法证明“如果一个三角形没有两个相等的角，那么这 个三角形不是等腰三角形”的第一步假设这个三角形是等腰三角形已知：在梯形ABCD中，AB//CD，∠C≠∠D求证：梯形ABCD不是等腰梯形.证明：假设梯形ABCD是等腰梯形。∴∠C=∠D（等腰梯形同一底上的两内角相等）这与已知条件∠C≠∠D矛盾, 假设不成立。∴梯形ABCD不是等腰梯形.

五、【课堂小结】

总结用反证法证明”在同一平面内,垂直于同一 条直线的两条直线互相平行.”