初中数学苏科版九年级上册第2章 对称图形——圆综合与测试同步达标检测题
展开圆--章节提优练习
一、选择题
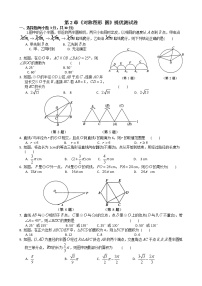
1. 如图,在菱形 ABCD 中,∠BAC=60∘,以顶点 B 为圆心,以 AB 长为半径画圆,延长 DC 交 ⊙B 于点 E,则 CE 的度数等于
A. 120∘ B. 90∘ C. 60∘ D. 30∘
2. 已知 ⊙O 的直径 CD=10 cm,AB 是 ⊙O 的弦,AB⊥CD,垂足为 M,且 AB=8 cm,则 AC 的长为
A.25 cm B.45 cm
C.25 cm 或 45 cm D.23 cm 或 43 cm
3. 如图,圆内接正六边形的边长为 4,以其各边为直径作半圆,则图中阴影部分的面积为
A. 243−4π B. 123+4π C. 243+8π D. 243+4π
4. 如图所示,⊙O 的半径为 13,弦 AB 的长度是 24,ON⊥AB,垂足为 N,则 ON=
A. 5 B. 7 C. 9 D. 11
5. 对于题目:“如图(1),平面上,正方形内有一长为 12 、宽为 6 的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数 n.”甲、乙、丙作了自认为边长最小的正方形,先求出该边长,再取最小整数 n.
甲:如图(2),思路是当 x 为矩形对角线长时就可移转过去;结果取 n=13.
乙:如图(3),思路是当 x 为矩形外接圆直径长时就可移转过去;结果取 n=14.
丙:如图(4),思路是当 x 为矩形的长与宽之和的 22 倍时就可移转过去;结果取 n=13.
下列正确的是
A.甲的思路错,他的 n 值对 B.乙的思路和他的 n 值都对
C.甲和丙的 n 值都对 D.甲、乙的思路都错,而丙的思路对
6. 如图,在四边形 ABCD 中,AB∥CD,AB=CD,∠B=60∘,AD=83,分别以 B 和 C 为圆心,以大于 12BC 的长为半径作弧,两弧相交于点 P 和 Q,直线 PQ 与 BA 延长线交于点 E,连接 CE,则 △BCE 的内切圆半径是
A. 4 B. 43 C. 2 D. 23
7. 如图,△ABC 是等腰直角三角形,AC=BC=a,以斜边 AB 上的点 O 为圆心的圆分别与 AC,BC 相切于点 E,F,与 AB 分别相交于点 G,H,且 EH 的延长线与 CB 的延长线交于点 D,则 CD 的长为
A. 22−12a B. 2+12a C. 2a D. 2−14a
8. 如图,矩形 ABCD 中,G 是 BC 的中点,过 A,D,G 三点的 ⊙O 与边 AB,CD 分别交于点 E,点 F,下列说法:① AC 与 BD 的交点是 ⊙O 的圆心;② AF 与 DE 的交点是 ⊙O 的圆心;③ BC 与 ⊙O 相切,其中正确说法的个数是
A. 0 B. 1 C. 2 D. 3
9. 如图,在等腰 △ABC 中,AB=AC=25,BC=8,按下列步骤作图:
①以点 A 为圆心,适当的长度为半径作弧,分别交 AB,AC 于点 E,F,再分别以点 E,F 为圆心,大于 12EF 的长为半径作弧相交于点 H,作射线 AH;
②分别以点 A,B 为圆心,大于 12AB 的长为半径作弧相交于点 M,N,作直线 MN,交射线 AH 于点 O;
③以点 O 为圆心,线段 OA 长为半径作圆.
则 ⊙O 的半径为
A. 25 B. 10 C. 4 D. 5
10. 如图所示,AB 是 ⊙O 的直径,弦 CD⊥AB,∠CDB=30∘,CD=23,则阴影部分图形的面积为
A.4π B.2π C.π D.2π3
二、填空题
11. 如图所示,若用半径为 8,圆心角为 120∘ 的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是 .
12. 如图,半圆的圆心与坐标原点重合,半圆的半径 1,直线 l 的解析式为 y=x+t.若直线 l 与半圆只有一个交点,则 t 的取值范围是 .
13. 如图是由两个长方形组成的工件平面图(单位:mm),直线 l 是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 mm.
14. 如图,等边三角形 ABC 内接于 ⊙O,点 D 在 ⊙O 上,∠ABD=25∘,则 ∠BAD= .
15. 已知 △ABC 的直角边 BC=1,斜边 AB=2,在直线 l 上如图所示位置开始滚动,第一次滚动绕 A 点旋转至线段 AB 与直线 l 重合,第二次绕 B 点滚动至线段 BC 与直线 l 重合,依此类推.当 △ABC 滚动一周时,点 B 移动的路程为 ,当 △ABC 滚动 2019 次时点 A 距它初始位置的长度为 .
16. 在 △ABC 中,若 AB=6,∠ACB=45∘.则 △ABC 的面积的最大值为 .
17. 如图直线 y=−x+mm>0 与 x 轴、 y 轴分别交于点 A,B,C 是 AB 的中点,点 D 在直线 y=−2 上,以 CD 为直径的圆与直线 AB 的另一交点为 E,交 y 轴于点 F,G,已知 CE+DE=62,FG=25,则 CD 的长是 .
18. 如图,在 △ABC 中,AC:BC:AB=5:12:13,⊙O 在 △ABC 内自由移动,若 ⊙O 的半径为 1,且圆心 O 在 △ABC 内所能到达的区域的面积为 152,则 △ABC 的周长为 .
三、解答题
19. 在 ⊙O 中,AB 为直径,C 为 ⊙O 上一点.
(1) 如图①,过点 C 作 ⊙O 的切线,与 AB 的延长线相交于点 P,若 ∠CAB=32∘,求 ∠P 的大小;
(2) 如图②,D 为优弧 ADC 上一点,且 DO 的延长线经过 AC 的中点 E,连接 DC 与 AB,相交于点 P,若 ∠CAB=16∘,求 ∠DPA 的大小.
20. 如图,AB 为 ⊙O 的直径,C 为 ⊙O 上一点,AD 和过 C 点的直线互相垂直,垂足为 D,且 AC 平分 ∠DAB.
(1) 求证:DC 为 ⊙O 的切线;
(2) 若 ⊙O 的半径为 3,AD=4,求 AC 的长.
21. 如图 1,AB 为 ⊙O 的直径,点 C 为 ⊙O 上一点,CD 平分 ∠ACB 交 ⊙O 于点 D,交 AB 于点 E.
(1) 求证:△ABD 为等腰直角三角形.
(2) 如图 2,ED 绕点 D 顺时针旋转 90∘,得到 DEʹ,连接 BEʹ,证明:BEʹ 为 ⊙O 的切线.
(3) 如图 3,点 F 为弧 BD 的中点,连接 AF,交 BD 于点 G,若 DF=1,求 AG 的长.
22. 如图,已知 AB 是 ⊙O 的直径,BC 是弦,弦 BD 平分 ∠ABC 交 AC 于 F,弦 DE⊥AB 于 H,交 AC于G.
(1) 求证:AG=GD;
(2) 当 ∠ABC 满足什么条件时,△DFG 是等边三角形?并说明理由.
23. 对于平面直角坐标系 xOy 中的点 P 和 ⊙C,给出如下定义:若 ⊙C 上存在点 A,使得 ∠APC=30∘,则称 P 为 ⊙C 的半角关联点.
当 ⊙O 的半径为 1 时,
(1) 在点 D12,−12,E2,0,F0,23 中,⊙O 的半角关联点是 ;
(2) 直线 l:y=−33x−2 交 x 轴于点 M,交 y 轴于点 N,若直线 l 上的点 Pm,n 是 ⊙O 的半角关联点,求 m 的取值范围.
24. 如图,在边长为 8 的正方形 ABCD 中,点 O 为 AD 上一动点 4
(1) 求证:△ODE∽△ECF.
(2) 在点 O 的运动过程中,设 DE=x:
①求 OD⋅CF 的最大值,并求此时 ⊙O 的半径长;
②判断 △CEF 的周长是否为定值?若是,求出 △CEF 的周长;否则,请说明理由.
25. 如图,抛物线 y=ax2+bx+ca≠0 与 x 轴交于点 A−4,0,B2,0,与 y 轴交于点 C0,4,线段 BC 的中垂线与对称轴 l 交于点 D,与 x 轴交于点 F,与 BC 交于点 E,对称轴 l 与 x 轴交于点 H.
(1) 求抛物线的函数表达式.
(2) 求点 D 的坐标.
(3) 点 P 为 x 轴上一点,⊙P 与直线 BC 相切于点 Q,与直线 DE 相切于点 R.求点 P 的坐标.
(4) 点 M 为 x 轴上方抛物线上的点,在对称轴 l 上是否存在一点 N,使得以点 D,P,M,N 为顶点的四边形是平行四边形?若存在,则直接写出 N 点坐标.若不存在,请说明理由.
26. 如图 1,点 E 是 △ABC 的内心,AE 的延长线交 BC 于点 F,交 △ABC 的外接圆 ⊙O 于点 D,连接 BD,过点 D 作直线 DM,使 ∠BDM=∠DAC.
(1) 求证:BC∥MD.
(2) 求证,直线 DM 是 ⊙O 的切线.
(3) 如图 2,若 AB 过圆心 O,BD=5,BC=8,求 △ABC 内切圆的半径长.
27. 已知:AB 是 ⊙O 的直径,PB 切 ⊙O 于点 B,AP 交 ⊙O 于点 C,D 是 ⊙O 上一点,连接 AD,CD.
(1) 如图 1,求证:∠APB=∠ADC;
(2) 如图 2,点 G 在 CD 上,∠CGB=∠BAD,OF⊥AC 于点 F,求证:BG=2OF;
(3) 如图 3,在(2)的条件下,连接 AG 并延长交 ⊙O 于点 H,若 CD 为 ⊙O 直径,当 ∠CGB=∠HGB,OF=3 时,求线段 GH 的长.
28. 对于平面直角坐标系 xOy 中的点 P 和 ⊙O,给出如下定义:若存在过点 P 的直线 l 交 ⊙O 于异于点 P 的 A,B 两点,在 P,A,B 三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点 P 为 ⊙O 的相邻点,直线 l 为 ⊙O 关于点 P 的相邻线.
(1) 当 ⊙O 的半径为 1 时,
① 分别判断在点 D12,14,E0,−3,F4,0 中,是 ⊙O 的相邻点有 ;
②请从 ① 中的答案中,任选一个相邻点,在图 1 中做出 ⊙O 关于它的一条相邻线,并说明你的作图过程.
③ 点 P 在直线 y=−x+3 上,若点 P 为 ⊙O 的相邻点,求点 P 横坐标的取值范围;
(2) ⊙O 的圆心在 x 轴上,半径为 1,直线 y=−33x+23 与 x 轴,y 轴分别交于点 M,N,若线段 MN 上存在 ⊙O 的相邻点 P,直接写出圆心 O 的横坐标的取值范围.
答案
一、选择题
1. 【答案】C
【知识点】弧、弦、圆心角的关系定理
2. 【答案】C
【解析】连接 AC,AO.
∵⊙O 的直径 CD=10 cm,AB⊥CD,AB=8 cm,
∴AM=12AB=12×8=4 cm,OD=OC=5 cm,
当 C 点位置如图所示时,
∵OA=5 cm,AM=4 cm,CD⊥AB,
∴OM=OA2−AM2=52−42=3 cm,
∴CM=OC+OM=5+3=8 cm,
∴AC=AM2+CM2=42+82=45 cm;
当 C 点位置如图所示时,同理可得 OM=3 cm,
∵OC=5 cm,
∴MC=5−3=2 cm,
在 Rt△AMC 中,AC=AM2+MC2=42+22=25 cm.
【知识点】垂径定理
3. 【答案】A
【知识点】扇形面积的计算
4. 【答案】A
【解析】由题意可得,ON⊥AB,OA=13,AB=24,
∴AN=12,
∴ON=OA2−AN2=132−122=5.
【知识点】垂径定理、勾股定理
5. 【答案】B
【知识点】勾股定理、三角形的外接圆与外心、矩形的性质
6. 【答案】A
【解析】 ∵ 在四边形 ABCD 中,AB∥CD,AB=CD,
∴ 四边形 ABCD 是平行四边形,
∴BC=AD=83,
由作图过程可得 EB=EC,
∵∠B=60∘,
∴△EBC 是等边三角形,
∴△BCE 的内切圆半径是 13×83×12×3=4.
【知识点】三角形的内切圆,内心
7. 【答案】B
【解析】 ∵△ABC 是等腰直角三角形,AC=BC=a,以斜边 AB 上的点 O 为圆心的圆分别与 AC,BC 相切于点 E,F,与 AB 分别相交于点 G,H,且 EH 的延长线与 CB 的延长线交于点 D,
∴ 连接 OE,OF,
由切线的性质可得 OE=OF=⊙O 的半径,∠OEC=∠OFC=∠C=90∘,
∴OECF 是正方形,
∵ 由 △ABC 的面积可知 12×AC×BC=12×AC×OE+12×BC×OF,
∴OE=OF=12a=EC=CF,BF=BC−CF=0.5a,GH=2OE=a,
∵ 由切割线定理可得 BF2=BH⋅BG,
∴14a2=BHBH+a,
∴BH=−1+22a 或 BH=−1−22a(舍去),
∵OE∥DB,OE=OH,
∴△OEH∽△BDH,
∴OEOH=BDBH,
∴BH=BD,CD=BC+BD=a+−1+22a=1+22a.
【知识点】切线的性质、基本定理、两角分别相等
8. 【答案】C
【解析】连接 DG,AG,作 GH⊥AD 于点 H,连接 OD,EF,如图.
∵G 是 BC 的中点,
∴AG=DG,
∴GH 垂直平分 AD,
∴ 点 O 在 HG 上.
∵AD∥BC,
∴HG⊥BC,
∴BC 与 ⊙O 相切,故③正确.
∵OG=OD,
∴O 不是 HG 的中点,
∴ 圆心 O 不是 AC 与 BD 的交点,故①不正确.
∵∠ADF=∠DAE=90∘,
∴∠AEF=90∘,
∴ 四边形 AEFD 为 ⊙O 的内接矩形,
∴AF 与 DE 的交点是 ⊙O 的圆心,故②正确.
【知识点】圆周角定理推论、切线的判定
9. 【答案】D
【解析】如图,设 OA 交 BC 于 T.
∵AB=AC=25,AO 平分 ∠BAC,
∴AO⊥BC,BT=TC=4,
∴AT=AC2−CT2=252−42=2,
在 Rt△OCT 中,则有 r2=r−22+42,解得 r=5.
【知识点】垂径定理
10. 【答案】D
【解析】设弦 CD 和直径 AB 相交于点 E,
因为弦 CD⊥AB,
所以 ∠OEC=∠BED=90∘,CE=DE=12CD=3.
又 ∠CDB=30∘,
所以 ∠COB=60∘,∠OCE=30∘,
所以 ∠OCE=∠BDE,
所以 △COE≌△DBE,
所以 S△COE=S△DBE,则阴影部分的面积等于扇形 OBC 的面积.
在 △COE 中,由勾股定理可得 OC=2,
所以 S阴影=S扇形OBC=60π×22360=2π3.
【知识点】垂径定理、弧长面积的计算、圆周角定理
二、填空题
11. 【答案】 83
【知识点】圆锥的计算
12. 【答案】 t=2 或 −1≤t<1
【解析】若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点 C 或从直线过点 A 开始到直线过点 B 结束(不包括直线过点 A).
直线 y=x+t 与 x 轴所形成的锐角是 45∘.
当直线和半圆相切于点 C 时,则 OC 垂直于直线,∠COD=45∘.
又 OC=1,则 CD=OD=22,即点 C−22,22,
把点 C 的坐标代入直线解析式,得 t=y−x=2,
当直线过点 A 时,把点 A−1,0 代入直线解析式,得 t=y−x=1.
当直线过点 B 时,把点 B1,0 代入直线解析式,得 t=y−x=−1.
即当 t=2 或 −1≤t<1 时,直线和圆只有一个公共点.
【知识点】勾股定理、切线的性质、一次函数的图象与性质
13. 【答案】 50
【解析】如图,设圆心为 O,连接 AO,CO,
∵ 直线 l 是它的对称轴,
∴CM=30,AN=40.
∵CM2+OM2=AN2+ON2,
∴302+OM2=402+70−OM2.
解得 OM=40.
∴OC=302+402=50.
∴ 能完全覆盖这个平面图形的圆面的最小半径是 50 mm.
【知识点】勾股定理、垂径定理
14. 【答案】 95°
【解析】 ∵△ABC 是等边三角形,
∴∠ABC=∠BAC=60∘.
∵∠ABD=25∘,
∴∠CBD=35∘.
∵CD=CD,
∴∠DAC=∠CBD=35∘.
∴∠BAD=60∘+35∘=95∘.
【知识点】等边三角形三个角相等,都等于60°、圆周角定理及其推理
15. 【答案】 136π ; 2019+6733
【解析】在 Rt△ACB 中,AB=2,BC=1,∠ACB=90∘,
∴AC=AB2−BC2=3,
∴sin∠BAC=BCAB=12,
∴∠BAC=30∘,
∴ 第一次旋转,点 B 移动的路程为 180−30π⋅AB180=5π×26=5π3,
第二次旋转以点 B 为旋转中心,
故点 B 没有移动,
第二次旋转以点 C 为旋转中心,旋转 90∘,
∴ 点 B 移动的路程为 90π⋅BC180=π2,
∴ 当 △ABC 滚动一周时,点 B 运动的路程为:5π3+π2=10π6+3π2=13π6,
∵△ABC 滚动一周需要滚动 3 次,
∴ 每滚动 3 次,点 A 距它的初始位置的长度为 1+2+3=3+3,
∵2019÷3=673.
∴ 当 △ABC 滚动 2019 次时,△ABC 向右滚动了 673 次,
∴673×3+3=2019+6733,
∴ 当 △ABC 滚动 2019 次时,点 A 距它初始位置的长度为 2019+6733.
【知识点】弧长的计算
16. 【答案】 92+9
【解析】作 △ABC 的外接圆 ⊙O,过 C 作 CM⊥AB 于 M.
∵ 弦 AB 已确定,
∴ 要使 △ABC 的面积最大,只要 CM 取最大值即可,
如图所示,当 CM 过圆心 O 时,CM 最大,
∵CM⊥AB,CM 过 O,
∴AM=BM(垂径定理),
∴AC=BC,
∵∠AOB=2∠ACB=2×45∘=90∘,
∴OM=AM=12AB=12×6=3,
∴OA=OM2+AM2=32,
∴CM=OC+OM=32+3,
∴S△ABC=12AB⋅CM=12×6×32+3=92+9.
【知识点】垂径定理、三角形的外接圆与外心、勾股定理
17. 【答案】 35
【解析】如图,设 CD 的中点为 Oʹ,设直线 BA 交直线 y=−2 于 M,直线 y=−2 交 y 轴于 P,作 CH⊥OB 于 H,连接 OʹF,作 AJ⊥DM 于 J,OʹN⊥FG 于 N.
∵CD 是 ⊙Oʹ 的直径,
∴∠CED=90∘,
∵ 直线 y=−x+mm>0 与 x 轴、 y 轴分别交于点 A,B,
∴Am,0,B0,m,
∴OA=OB,
∴∠OAB=45∘,
∵OA∥DM,
∴∠EMD=∠OAB=45∘,
∵∠DEM=90∘,
∴ED=EM,
∴EC+ED=EC+EM=CM=62,
∵JA⊥DM,
∴∠AJM=90∘,
∴AJ=JM=2,
AM=22,
∴BC=CA=42,
∴AB=82,
∴BO=AO=8,
∴A8,0,B0,8,C4,4,
设 Dm,−2,则 Oʹ12m+4,1,
∴OʹN=12m+4,OʹF=12CD=12m−42+62,
∵OʹN⊥FG,
∴FN=12FG=5.
在 Rt△OʹFN 中,由勾股定理,得:52+14m+42=14m−42+62.
解得:m=1.
∴CD=1−42+62=35.
【知识点】勾股定理、一次函数的解析式、圆周角定理及其推理
18. 【答案】 30
【解析】如图,由题意点 O 所能到达的区域是 △EFG,连接 AE,延长 AE 交 BC 于 H,作 HM⊥AB 于 M,EK⊥AC 于 K,作 FJ⊥AC 于 J.
因为 EG∥AB,EF∥AC,FG∥BC,
所以 ∠EGF=∠ABC,∠FEG=∠CAB,
所以 △EFG∽△ACB,
所以 EF:FG:EG=AC:BC:AB=5:12:13,
设 EF=5k,FG=12k,
因为 12×5k×12k=152,
所以 k=12或−12(舍弃),
所以 EF=52,
因为四边形 EKJF 是矩形,
所以 KJ=EF=52,
设 AC=5m,BC=12m,AB=13m,
因为 ∠ACH=∠AMH=90∘,∠HAC=∠HAM,AH=AH,
所以 △HAC≌△HAMAAS,
所以 AM=AC=5m,CH=HM,BM=8m,设 CH=HM=x,
在 Rt△BHM 中,则有 x2+8m2=12m−x2,
所以 x=103m,
因为 EK∥CH,
所以 EKCH=AKAC,
所以 1103m=AK5m,
所以 AK=32,
所以 AC=AK+KJ+CJ=32+52+1=5,
所以 BC=15×5×12=12,AB=15×5×13=13,
所以 △ABC 的周长 =AC+BC+AB=5+12+13=30.
【知识点】性质与判定综合(D)、切线的性质、性质与判定综合(D)
三、解答题
19. 【答案】
(1) 连接 OC,如图①,
∵PC 为切线,
∴OC⊥PC,
∴∠OCP=90∘,
∵OA=OC,
∴∠OCA=∠CAB=32∘,
∴∠POC=∠OCA+∠CAB=64∘,
∴∠P=90∘−∠POC=90∘−64∘=26∘.
(2) 如图②,
∵ 点 E 为 AC 的中点,
∴OD⊥AC,
∴∠OEA=90∘,
∴∠AOD=∠CAB+∠OEA=16∘+90∘=106∘,
∴∠C=12∠AOD=53∘,
∴∠DPA=∠BAC+∠C=16∘+53∘=69∘.
【知识点】切线的性质、三角形的外角及外角性质、垂径定理
20. 【答案】
(1) 如图,连接 OC,
∵ OA=OC,
∴ ∠OAC=∠OCA.
∵ AC 平分 ∠DAB,
∴ ∠DAC=∠OAC.
∴ ∠DAC=∠OCA.
∴ OC∥AD.
∵ AD⊥CD,
∴ OC⊥CD.
∵ OC 是 ⊙O 的半径,
∴ DC 为 ⊙O 的切线;
(2) 如图,连接 BC,则 ∠ACB=90∘,
∵ ∠DAC=∠OAC,∠ADC=∠ACB=90∘,
∴ △ADC∽△ACB.
∴ ADAC=ACAB.
∴ AC2=AD⋅AB.
∵ ⊙O 的半径为 3,AD=4,
∴ AB=6.
∴ AC=26.
【知识点】圆周角定理推论、两角分别相等、切线的判定
21. 【答案】
(1) ∵AB 是 ⊙O 的直径,
∴∠ADB=∠ADB=90∘,
∵CD 平分 ∠ACB,
∴AD=BD,
∴AD=BD,
∴△ABD 是等腰直角三角形.
(2) 由旋转的性质得,∠EDEʹ=90∘,DE=DEʹ,
∵∠ADB=90∘,
∴∠ADE=∠BDEʹ,
∵AD=BD,
∴△ADE≌△BDEʹSAS,
∴∠DAE=∠DBEʹ,
∵∠EAD=∠DCB=45∘,∠ABD=∠DCA=45∘,
∴∠OBE=∠ABD+∠DBEʹ=90∘,
∴BEʹ 为 ⊙O 的切线.
(3) ∵ 点 F 为 BD 的中点,
∴∠FAD=12∠DAB=22.5∘,
取 AG 的中点 H,连接 DH,
∵∠ADB=90∘,
∴DH=AH=GH,
∴∠ADH=∠FAD=22.5∘,
∴∠DHF=∠ADH+∠FAD=45∘,
∵∠AFD=∠ACD=45∘,
∴∠DHF=∠AFD,
∴DH=DF=1,
∴AG=2DH=2.
【知识点】弧、弦、圆心角的关系定理、切线的判定、边角边、圆周角定理及其推理、直角三角形斜边的中线、等腰直角三角形
22. 【答案】
(1) 连接 AD,
∵ DE⊥AB,AB 是 ⊙O 的直径,
∴ AD=AE,
∴ ∠ADE=∠ABD.
∵ 弦 BD 平分 ∠ABC,
∴ ∠DBC=∠ABD.
∵ ∠DBC=∠DAC,
∴ ∠ADE=∠DAC,
∴ AG=GD.
(2) 当 ∠ABC=60∘ 时,△DFG 是等边三角形.
理由:
∵ 弦 BD 平分 ∠ABC,
∴ ∠DBC=∠ABD=30∘.
∵ AB 是 ⊙O 的直径,
∴ ∠ACB=90∘,
∴ ∠CAB=90∘−∠ABC=30∘,
∴ ∠DFG=∠FAB+∠DBA=60∘.
∵ DE⊥AB,
∴ ∠DGF=∠AGH=90∘−∠CAB=60∘,
∴ △DGF 是等边三角形.
【知识点】垂径定理、圆周角定理、等边三角形
23. 【答案】
(1) D,E
(2) 由直线 l 的解析式得 M−23,0,N0,−2,
以 O 为圆心,ON 长为半径画圆,交直线 MN 于点 G,
可得 m≤0,
设小圆 ⊙O 与 y 轴负半轴的交点为 H,
连接 OG,HG,
∵M−23,0,N0,−2,
∴OM=23,ON=2,
∴tan∠OMN=33,
∴∠OMN=30∘,∠ONM=60∘,
∴△OGN 是等边三角形,
∴GH⊥y 轴,
∴ 点 G 的纵坐标为 −1,代入 y=−33x−2 可得,横坐标为 −3,
∴m≥−3,
∴−3≤m≤0.
【知识点】圆的定义、特殊角的正切值、30度所对的直角边等于斜边的一半、一次函数与一元一次方程的关系
24. 【答案】
(1) ∵EF 切 ⊙O 于点 E,
∴∠OEF=90∘,
∴∠OED+∠CEF=90∘,
∵∠C=90∘,
∴∠CEF+∠CFE=90∘,
∴∠OED=∠EFC,
∵∠D=∠C=90∘ ,
∴△ODE∽△ECF.
(2) ①由(1):△ODE∽△ECF,
∴ODEC=DECF,
∴OD⋅CF=DE⋅EC,
∵DE=x,
∴EC=8−x,
∴OD⋅CF=x8−x=−x2+8x=−x−42+16,
当 x=4 时,OD⋅CF 的值最大,最大值为 16,
设此时半径为 r,则 OA=OE=r,OD=8−r,
在 Rt△ODE 中,
∵OD2+DE2=OE2,
∴8−r2+42=r2,
解得 r=5.
即此时半径长为5.
② △CEF 的周长为定值,△CEF 的周长 =16,
在 Rt△ODE 中,OD2+DE2=OE2,OA=OE,
即:8−OE2+x2=OE2,
∴OE=4+x216,OD=8−OE=4−x216,
∵Rt△DOE∽Rt△CEF,
即 ODEC=DECF=OEEF,
∴4−x2168−x=xCF=4+x216EF,
解得 CF=16x8+x,EF=64+x28+x,
∴△CEF 的周长 =CE+CF+EF=8−x+16x8+x+64+x28+x=16.
【知识点】相似三角形的性质、切线的性质、两角分别相等、勾股定理
25. 【答案】
(1) ∵ 抛物线过点 A−4,0,B2,0,
∴ 设抛物线表达式为:y=ax+4x−2,
把 C0,4 代入得,
4=a0+40−2,
∴a=−12,
∴ 抛物线表达式为:y=−12x+4x−2=−12x2−x+4.
(2) 由(1)抛物线对称轴为直线 x=−b2a=−1,
∵ 线段 BC 的中垂线与对称轴 l 交于点 D,
∴ 点 D 在对称轴上,
设点 D 坐标为 −1,m,
过点 C 作 CG⊥l 于 G,连 DC,DB,
∴DC=DB,
在 Rt△DCG 和 Rt△DBH 中,
∵DC2=12+4−m2,DB2=m2+2+12,
∴12+4−m2=m2+2+12,
解得:m=1,
∴ 点 D 坐标为 −1,1.
(3) ∵ 点 B 坐标为 2,0,C 点坐标为 0,4,
∴BC=22+42=25,
∵EF 为 BC 中垂线,
∴BE=5,
在 Rt△BEF 和 Rt△BOC 中,
cos∠CBF=BEBF=OBBC,
∴5BF=225,
∴BF=5,EF=BF2−BE2=25,OF=3,
设 ⊙P 的半径为 r,⊙P 与直线 BC 和 EF 都相切,
如图:
①当圆心 P1 在直线 BC 左侧时,连 P1Q1,P1R1,则 P1Q1=P1R1=r1,
∴∠P1Q1E=∠P1R1E=∠R1EQ1=90∘,
∴ 四边形 P1Q1ER1 是正方形,
∴ER1=P1Q1=r1,
在 Rt△BEF 和 Rt△FR1P1 中,
tan∠1=BEBF=P1R1FR1,
∴525=r125−r1,
∴r1=253,
∵sin∠1=BEBF=P1R1FP1,
∴FP1=103,OP1=13,
∴ 点 P1 坐标为 13,0.
②同理,当圆心 P2 在直线 BC 右侧时,
可求 r2=25,OP2=7,
∴P2 坐标为 7,0,
∴ 点 P 坐标为 13,0 或 7,0.
(4) −1,8318,−1,4718,−1,−4718.
【解析】
(4) 存在.
当点 P 坐标为 13,0 时,
①若 DN 和 MP 为平行四边形对边,则有 DN=MP,
当 x=13 时,y=−12132−13+4=6518,
∴DN=MP=6518,
∴ 点 N 坐标为 −1,8318.
②若 MN,DP 为平行四边形对边时,M,P 点到 ND 距离相等,
则点 M 横坐标为 −73,
则 M 纵坐标为 −12×−322+73+4=6518,
由平行四边形中心对称性可知,点 M 到 N 的垂直距离等于点 P 到点 D 的垂直距离,
当点 N 在 D 点上方时,点 N 纵坐标为 6518−1=4718,
此时点 N 坐标为 −1,4718,
当点 N 在 x 轴下方时,点 N 坐标为 −1,−4718,
当点 P 坐标为 7,0 时,所求 N 点不存在.
【知识点】切线的性质、平行四边形及其性质、二次函数的解析式、勾股定理
26. 【答案】
(1) ∵∠BDM=∠DAC,
∠DAC=∠DBC,
∴∠BDM=∠DBC,
∴BC∥MD.
(2) 连接 OD,OB,OC,DC.
∵ 点 E 是 △ABC 的内心,
∴AF 平分 ∠BAC,
∴∠BAD=∠CAD,
∴BD=CD,
∴BD=CD,
又 OB=OC,
∴OD 垂直平分 BC,
∴OD⊥BC,
∵BC∥MD,
∴OD⊥MD,
∴ 直线 DM 是 ⊙O 的切线.
(3) 设 OD 与 BC 交于 G.
∵OD⊥BC,BC=8,
∴BG=12BC=4,
∵BD=5,
∴DG=BD2−BG2=52−42=3,
设 ⊙O 的半径为 r,则 OB=r,OG=r−3,
Rt△OBG 中,OB2=BG2+OG2,
∴r2=42+r−32,解得 r=256,
∴AB=2r=253,
OG=256−3=76,
∵OA=OB,BG=CG,
∴AC=2OG=73,
∵AB 为直径,
∴∠C=90∘,
∴Rt△ABC 内切圆的半径长为 BC+AC−AB2=8+73−2532=1.
【知识点】圆周角定理推论、垂径定理、切线的判定
27. 【答案】
(1) 如图 1 中,连接 BC.
∵PB 是 ⊙O 的切线,
∴AB⊥PB,
∴∠ABP=90∘,
∵AB 是直径,
∴∠ACB=90∘,
∵∠P+∠PBC=90∘,∠PBC+∠ABC=90∘,
∴∠P=∠ABC,
∵∠ADC=∠ABC,
∴∠P=∠ADC.
(2) 如图 2 中,连接 BC.
∵OF⊥AC,
∴AF=CF,
∵OA=OB,
∴BC=2OF,
∵∠CGB=∠BAD,∠BCD=∠BAD,
∴∠BCG=∠BGC,
∴BG=BC=2OF.
(3) 如图 3 中,连接 BC,BH,作 BM⊥CD 于 M,AN⊥CD 于 N.
∵CD,AB 是直径,
∴OA=OD=OC=OB,
∵∠AOD=∠BOC,
∴△AOD≌△BOCSAS,
∴AD=BC=2OF=6,
∵OA=OB,∠AON=∠BOM,∠ANO=∠BMO=90∘,
∴△AON≌△BOMAAS,
∴OM=ON,AN=BM,设 OM=ON=a,
∵∠CGB=∠HGB,
∴∠OGH=2∠CGB,
∵∠BOG=∠OCB+∠OBC=2∠GCB,∠GCB=∠BGC,
∴∠BOG=∠OGH,
∴∠AOG=∠AGO,
∴AO=AG,
∵AN⊥OG,
∴ON=NG=a,
∵BG=AD,BM=AN,∠AND=∠BMG=90∘,
∴Rt△BMG≌Rt△ANDHL,
∴MG=DN=3a,OD=OA=OB=OC=4a,
∴BM=OB2−OM2=15a,
在 Rt△CBM 中,
∵BC2=BM2+CM2,
∴36=15a2+9a2,
∵a>0,
∴a=62,
∴MG=3a=362,
∵∠BGH=∠BGM,∠BMG=∠H=90∘,BG=BG,
∴△BGH≌△BGMAAS,
∴GH=MG=362.
【知识点】圆周角定理及其推理、等腰三角形的判定、切线的性质、垂径定理
28. 【答案】
(1) ① D,E
②连接 OD,过 D 作 OD 的垂线交 ⊙O 于 A,B 两点.
③因为 ⊙O 的半径为 1,所以点 P 到 ⊙O 的距离小于等于 3,且不等于 1 时时,符合题意.
因为点 P 在直线 y=−x+3 上,
所以 0≤xp≤3.
(2) 0≤xo≤9
【知识点】一次函数的解析式、圆的相关元素
苏科版九年级上册第2章 对称图形——圆综合与测试达标测试: 这是一份苏科版九年级上册第2章 对称图形——圆综合与测试达标测试,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学苏科版九年级上册第2章 对称图形——圆综合与测试练习题: 这是一份初中数学苏科版九年级上册第2章 对称图形——圆综合与测试练习题,共36页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学苏科版九年级上册第2章 对称图形——圆综合与测试同步达标检测题: 这是一份初中数学苏科版九年级上册第2章 对称图形——圆综合与测试同步达标检测题,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。