数学北师大版 (2019)4.1 函数的奇偶性学案

函数的奇偶性

【学习目标】

（1）理解、掌握函数奇偶性的概念、图象特征和性质；

（2）能够根据定义和图像判断简单函数的奇偶性；

（3）能够应用定义证明和解决与函数的奇偶性有关的问题。

【学习重难点】

（1）函数奇偶性的概念、图象特征和性质；

（2）根据定义和图像判断简单函数的奇偶性；

（3）用定义证明和解决与函数的奇偶性有关的问题。

【学习过程】

一、知识引入

在日常生活中，我们经常会看到一些具有对称性的图片，如美丽的蝴蝶、精彩的剪纸等等。

思考讨论：

（1）上列各图，分别是怎样的对称图形？

（2）在我们学习的函数中，有些函数的图象也具有对称性，请举出几个这样的函数；

例1.画出函数的图象，并观察它的对称性.

（3）上例函数的图象是关于原点中心对称的，你能说出函数解析式是怎样体现这个性质的吗？

二、新知识

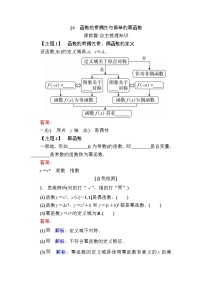
一般地，设函数定义域为.

如果当时,有，且，那么就称函数为奇函数；

如果当时,有，且，那么就称函数为偶函数。

如：函数、等等

注意：

①当函数是奇函数或偶函数时，称函数具有奇偶性。

奇函数图象关于原点中心对称，反之亦然；

偶函数图象关于轴对称,反之亦然。

②函数具有奇偶性的前提是：定义域关于原点对称；

③若奇函数是在处有定义，则有；

④如果已知了一个函数的奇偶性，那么在研究它的性质时，可以先研究其在非负区间上的性质，然后利用对称性可得在轴另一侧函数的性质.

例2.根据定义，判断下列函数的奇偶性：

（1）；

（2）；

（3）；

（4）.

思考讨论（综合练习）

（1）根据定义，判断下列函数的奇偶性：

①

②

③

④

（2）已知函数是定义在上的奇函数，且当时，.

①求函数的解析式；

②若函数在上单调递增，求实数的取值范围.

注意：

①奇偶性的定义是判断函数奇偶性的基本方法，某些函数，如果不易直接看出的关系，可以通过验证或来判断函数的奇偶性；

②奇函数如果在处有定义，必有；

③函数在定义域内，如果满足，则函数图象关于直线对称；如果满足，则函数图象关于直线对称.