数学必修 第一册3 函数的单调性和最值学案设计
展开函数的单调性和最值
【第一课时】
【学习目标】
(1)利用图象判断函数的单调性、寻找函数的单调区间;
(2)掌握函数的单调性的定义,用定义证明函数的单调性,及作差结果符号的判断方法;
(3)熟悉常见函数(绝对值函数、二次函数、分段函数等)的单调性及简单应用。
【学习重难点】
(1)利用函数的图象判断单调性、寻找函数单调区间;
(2)函数的单调性的定义,用定义证明函数的单调性的方法,及作差结果符号的判断方法;
(3)常见函数(绝对值函数、二次函数、分段函数等)的单调性及简单应用。
【学习过程】
一、知识引入
初中学习了一次函数的图象和性质.
当时,直线是向右上,即函数值随的增大而__________,
当时,直线向右下,即函数值随的增大而__________。
思考讨论:
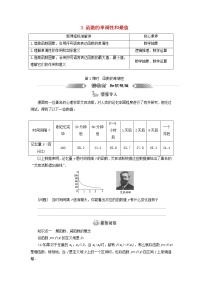
(1)如图,是某位同学从高一到高三上学期的考试成绩的统计图,从图中,你可以得出该同学成绩是怎样变化的呢?
(2)如图,是函数的图象,说出在各个区间函数值随的值的变化情况.
二、新知识
一般地,在函数定义域内的一个区间上.
如果对于任意的,当时,都有___________,那么就称函数在区间上是增函数或递增的;
如果对于任意的,当时,都有____________,那么就称函数在区间上是减函数或递减的。
注意:
①函数在区间上是增函数(减函数),那么就称函数在区间上是单调函数,或称在区间上具有单调性,区间称为函数的单调区间。
如:一元二次函数在区间上是__________(单调递增),区间是函数的__________区间;
②增函数的图象是上升的,减函数的图象是下降的;
③“函数在区间上单增”与“函数的单增区间是”两种叙述含义是不同的.
如:函数的单调递增区间为,则对称轴__________;
函数在区间上单调递增,则对称轴__________.
④函数的定义域为,由函数图象可知,在两个区间上函数都是单调递减的,但不能说成“函数在定义域内递减”或“函数的单调递减区间是”,而只能说“函数在区间和区间上都是递减的”.
例1.设,画出函数的图象,并通过图象直观判断它的单调性.
例2.根据函数图象直观判断的单调性.
例3.判断函数的单调性,并给出证明.
思考讨论(综合练习)
(1)二次函数在区间上单调,则实数的取值范围;
(2)设函数,证明:当时,函数在区间上是减函数;
(3)已知,函数是区间上的单调函数,求实数的取值范围;
(4)设实数,函数在区间上的最小值是,求并画出的图象.
【第二课时】
【学习目标】
(1)利用函数的单调性定义证明函数的单调性;
(2)复杂函数(双曲函数、分式函数、复合函数等)单调性的分析和证明;
(3)熟练利用函数的单调性解决函数、不等式等问题。
【学习重难点】
(1)利用定义证明函数的单调性;
(2)复杂函数(双曲函数、分式函数、复合函数等)单调性的分析和证明;
(3)利用函数的单调性解决函数、不等式等问题。
【学习过程】
思考讨论:
(1)增函数和减函数的定义是什么?
(2)如果有两个函数和,在同一个区间上都是单增(单减)函数,那么函数的具有怎样的单调性?能不能判断函数的单调性呢?
例4.判断函数的单调性,并给出证明.
例5.试用定义证明:函数在区间上是减函数,在区间上是增函数.
注意:
①函数在区间上是减函数,在区间上是增函数.
时,由函数的单调性或由均值不等式,可得当时,函数取得最小值,同理也可以得到时函数的单调性。画出该函数的图象,如图,该函数又叫双曲函数.
形如的函数,在区间上也具有类似的性质,根据均值不等式,可得当__________时,函数取得最小值__________,函数在区间上是__________,在区间上是__________;
②设是的函数,是的函数,其中函数的值域是函数的定义域或子集,则函数称为函数与函数的复合函数。
复合函数单调性常采用分层分析的方法:
如:函数,令,则
当时,,所以函数在时单减,
当时,,所以函数在时单增,
其中“”代表增大,“”代表减小.
③有些函数问题中(如求值域、求最值等),如果要用到函数的单调性,而又不需证明,可以通过分析的方法,得到函数的单调性.
如:求函数在区间上的最值.
____________________________________,
当时,随着,,所以函数,即函数单增.
所以____________________,____________________。
思考讨论(综合练习)
(1)如果函数,对任意实数都有,试比较、、的大小;
(2)函数在上单调递增,求实数的取值范围
(3)求函数的单调区间;
(4)已知定义在区间上的函数,满足:i)对任意,都有;ii)当时,.
①判断并证明单调性;
②解关于的不等式.
高中数学北师大版 (2019)必修 第一册3 函数的单调性和最值导学案: 这是一份高中数学北师大版 (2019)必修 第一册3 函数的单调性和最值导学案,共10页。
湘教版(2019)必修 第一册3.2 函数的基本性质学案设计: 这是一份湘教版(2019)必修 第一册3.2 函数的基本性质学案设计,共8页。
高中北师大版 (2019)第二章 函数3 函数的单调性和最值第2课时导学案: 这是一份高中北师大版 (2019)第二章 函数3 函数的单调性和最值第2课时导学案,共6页。