第六章统计单元测试题-2020-2021学年高一数学新教材配套学案（北师大2019版必修第一册）

第六章统计单元测试题

第I卷（选择题）

请点击修改第I卷的文字说明

一、单选题

1．为了解某地参加计算机水平测试的5000名学生的成绩，从中抽取了200名学生的成绩进行统计分析，在这个问题中，5000名学生成绩的全体是（  ）

A．总体 B．个体 C．从总体中抽取的一个样本 D．样本的容量

2．在某技能测试中，甲乙两人的成绩（单位：分）记录在如下的茎叶图中，其中甲的某次成绩不清晰，用字母代替．已知甲乙成绩的平均数相等，那么甲乙成绩的中位数分别为（    ）

A．20    20 B．21    20 C．20    21 D．21    21

3．从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分步直方图如图，则用电度数的中位数约为（    ）

A．150 B．177.8 C．183.3 D．200

4．清远市教育教学研究院想了解清远市某所中学的学生是否赞成该学校的某个新政策，由于条件限制，教学研究院不能询问每位学生的意见，所以需要选择一个合适的样本.最好的方法是询问(    )

A．由该学校推选的学生

B．在课间遇见的学生

C．在图书馆学习的学生

D．从学校名单中随机选取的学生

5．为了解某种轮胎的性能，随机抽取了8个进行测试，其最远里程数（单位：）为：96，102，99，108，99，114，88，97，则他们的中位数是（    ）

A．100 B．99 C．98.5 D．98

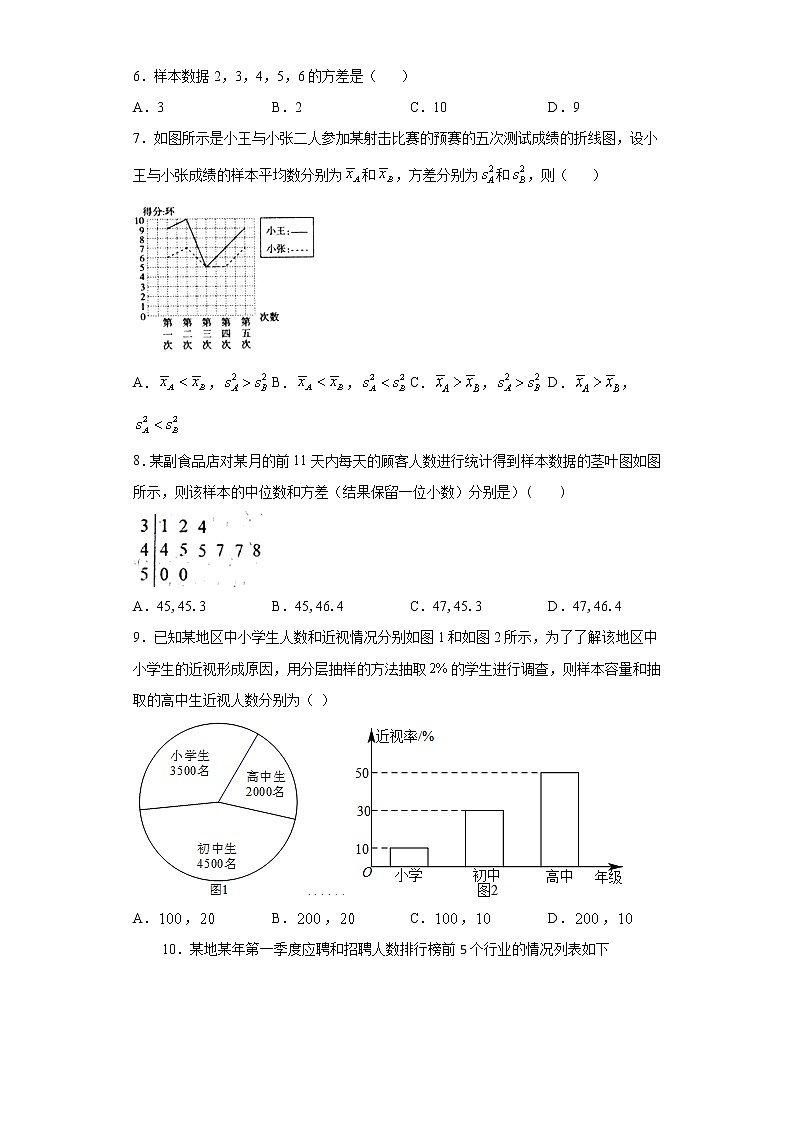
6．样本数据2，3，4，5，6的方差是（    ）

A．3 B．2 C．10 D．9

7．如图所示是小王与小张二人参加某射击比赛的预赛的五次测试成绩的折线图，设小王与小张成绩的样本平均数分别为和，方差分别为和，则（    ）

A．， B．， C．， D．，

8．某副食品店对某月的前11天内每天的顾客人数进行统计得到样本数据的茎叶图如图所示，则该样本的中位数和方差（结果保留一位小数）分别是）(    )

A．45,45.3 B．45,46.4 C．47,45.3 D．47,46.4

9．已知某地区中小学生人数和近视情况分别如图1和如图2所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取的学生进行调查，则样本容量和抽取的高中生近视人数分别为（ ）

A．， B．， C．， D．，

10．某地某年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下

若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是(    )

A．计算机行业好于化工行业. B．建筑行业好于物流行业.

C．机械行业最紧张. D．营销行业比贸易行业紧张.

11．若某位同学次数学成绩和次语文成绩的茎叶图如图，则该同学的数学成绩平均分与语文成绩的中位数分别为（    ）

A． B． C． D．

12．已知一组数据、、、、的平均数是，方差是，那么另一组数、、、、的平均数，方差分别是（    ）

A． B． C． D．

第II卷（非选择题）

请点击修改第II卷的文字说明

二、填空题

13．已知样本2，，，4，6的平均数为4，则标准差的最小值为______．

14．对某商店一个月（天）内每天的顾客人数进行了统计，得到样本的茎叶图（如图所示），则该样本的众数是______.

15．采用简单随机抽样从含10个个体的总体中抽取一个容量为4的样本,若个体a前两次未被抽到,则第三次被抽到的概率为_____.

16．图是甲、乙两人在次综合测评中的成绩的茎叶图，其中一个数字被污损；则甲的平均成绩超过乙的平均成绩的概率为       .

三、解答题

17．某校从参加某次知识竞赛测试得学生中随机抽取60名学生，将其成绩（百分制均为整数）分成6段，，…，后得到如下部分频率直方分布图，观察图形得信息，回答下列问题：

（1）求分数在内的频率；

（2）若用样本估计总体，已知该校参加知识竞赛一共有300人，请估计本次考试成绩不低于80分的人数；

（3）统计方法中，同一组数据常用该组区间中点值作为代表，据此估计本次考试的平均分.

18．某良种培育基地正在培育一种小麦新品种A.将其与原有的一个优良品种B进行对照试验．两种小麦各种植了25亩，所得亩产数据(单位：千克)如下：

品种A：357,359,367,368,375,388,392,399,400,405,412, 414,415,421,423,423,427,430,430,434,443,445,445,451,454

品种B：363,371,374,383,385,386,391,392,394,394,395, 397,397,400,401,401,403,406,407,410,412,415,416,422,430

(1)作出茎叶图；

(2)通过观察茎叶图，对品种A与B的亩产量及其稳定性进行比较，写出统计结论．

19．从一批产品中随机抽取件测量其内径，将测得数据进行统计整理后得到如下图所示的频率分布直方图.

（Ⅰ）求这件产品中，内径在内的产品数量；

（Ⅱ）试估计这批产品内径的中位数；

（Ⅲ）直接比较这批产品内径的平均数与（单位毫米）的大小关系，不必说明理由.

20．从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量表得如下频数分布表：

（I）在答题卡上作出这些数据的频率分布直方图：

（II）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）；

（III）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？

21．某蛋糕店计划按天生产一种面包，每天生产量相同，生产成本每个6元，售价每个8元，未售出的面包降价处理，以每个5元的价格当天全部处理完.

（1）若该蛋糕店一天生产30个这种面包，求当天的利润y（单位：元）关于当天需求量n（单位：个，）的函数解析式；

（2）蛋糕店记录了30天这种面包的日需求量（单位：个），整理得表：

假设蛋糕店在这30天内每天生产30个这种面包，求这30天的日利润（单位：元）的平均数及方差；

（3）蛋糕店规定：若连续10天的日需求量都不超过10个，则立即停止这种面包的生产，现给出连续10天日需求量的统计数据为“平均数为6，方差为2”，试根据该统计数据决策是否一定要停止这种面包的生产？并给出理由.

22．某学校因为寒假延期开学，根据教育部停课不停学的指示，该学校组织学生线上教学，高一年级在线上教学一个月后，为了了解线上教学的效果，在线上组织了数学学科考试，随机抽取50名学生的成绩并制成频率分布直方图如图所示.

（1）求m的值，并估计高一年级所有学生数学成绩在分的学生所占的百分比；

（2）分别估计这50名学生数学成绩的平均数和中位数.（同一组中的数据以该组区间的中点值作代表，结果精确到0.1）

参考答案

1．A

【解析】

试题分析：由题意得，根据抽样的概念可知，这名学生成绩的全体是样本的总体，故选A.

考点：抽样的概念.

2．B

【解析】

【分析】

先由题中数据，根据题意，求出，将甲乙的成绩都从小到大排序，即可得出中位数.

【详解】

由题中数据可得：甲的平均数为，

乙的平均数为，

因为甲乙成绩的平均数相等，所以，解得：，

所以甲的成绩为：，其中位数为，

乙的成绩为：，其中位数为.

故选：B.

【点睛】

本题主要考查由茎叶图计算中位数，属于基础题型.

3．C

【解析】

【分析】

确定出用电量从少到多频率和为0.5所在的区间，再求出占该区间的比例，即可求解.

【详解】

因有50%的个体小于或等于中位数，

小于150的个体频率为，

150-200之间的频率，

所以中位数为150-200之间的处，即.

故选：C.

【点睛】

本题考查由频率直方图求中位数，属于基础题.

4．D

【解析】

【分析】

根据抽样的原则，确定正确选项.

【详解】

按照随机的原则，即保证总体中每一个对象都有已知的、非零的概率被选入作为研究的对象，保证样本的代表性。随机抽样法就是调查对象总体中每个部分都有同等被抽中的可能，是一种完全依照机会均等的原则进行的抽样调查，被称为是一种“等概率”。ABC三个抽样方法，不能保证等可能，D选项可以保证等可能，所以最好的方法是D.

故选：D

【点睛】

本小题主要考查随机抽样的等可能性，属于基础题.

5．B

【解析】

【分析】

根据中位数的定义即可求出．

【详解】

将题目中8个数据按照从小到大的顺序排列，得到88，96，97，99，99，102，108，114，

按照中位数的定义可知，最中间的两个数据99，99的平均数99即为中位数.

故选：B.

【点睛】

本题主要考查中位数的定义的理解和应用，属于容易题．

6．B

【解析】

【分析】

根据题目中的数据可以求得这组数据的平均数，然后根据方差计算公式可以解答本题．

【详解】

，.

故选：B．

【点睛】

本题考查方差，解题的关键是明确题意，会利用方差公式计算一组数据的方差．

7．C

【解析】

【分析】

根据图形分析数据的整体水平和分散程度.

【详解】

观察题图可知，实线中的数据都大于或等于虚线中的数据，所以小王成绩的平均数大于小张成绩的平均数，即；

显然实线中的数据波动都大于或等于虚线中的数据波动，所以小王成绩的方差大于小张成绩的方差，即.

故选：C.

【点睛】

此题考查根据数据特征辨析平均数和方差，关键在于准确分析图形反映的数据特征而并非计算.

8．B

【解析】

【分析】

根据茎叶图中数据及中位数,方差的概念进行计算可得答案.

【详解】

由题中茎叶图共有11个数据,所以中位数为45,平均数为,求得方差为46.4.

故选:B.

【点睛】

本题主要考查茎叶图的相关知识,及中位数,方差的相关概念,考查学生的计算能力,难度一般.

9．B

【解析】

【分析】

【详解】

试题分析：由题意知，样本容量为，其中高中生人数为，

高中生的近视人数为，故选B.

【考点定位】

本题考查分层抽样与统计图，属于中等题.

10．B

【解析】

∵用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况，

∴建筑行业招聘人数是76516，而应聘人数没有排在前五位，小于65280，

建筑行业人才是供不应求，

∵物流行业应聘人数是74570，

而招聘人数不在前五位，要小于70436，

∴物流行业是供大于求，

∴就业形势是建筑行业好于物流行业，

故选B.

11．C

【解析】

【分析】

根据茎叶图提供的数据分别计算数学成绩的平均值、语文成绩的中位数即可.

【详解】

由茎叶图知，

5次数学成绩的平均分为(分)，

语文成绩的中位数为

故选：C

【点睛】

本题主要考查了茎叶图，平均数，中位数，属于容易题.

12．C

【解析】

【分析】

利用平均数和方差公式可得出结果.

【详解】

由题意可得，

，

则新数据的平均数为，

方差为.

故选：C.

【点睛】

本题考查平均数与方差的计算，熟练利用公式是解答的关键，考查计算能力，属于基础题.

13．

【解析】

【分析】

由已知可得，先求标准差的平方即方差的最小值，根据方差公式，用表示，转化为求关于的二次函数最小值，即可求解.

【详解】

样本2，，，4，6的平均数为4，

所以，设标准差为，

,

当时，取最小值为，

所以标准差的最小值为.

故答案为:.

【点睛】

本题考查样本的平均数、标准差，考查二次函数的最值，属于基础题.

14．45

【解析】

【分析】

直接利用茎叶图，求出该样本的众数即可.

【详解】

由题意可知茎叶图共有30个数值，出现次数最多的数是45，

故众数是45，

故答案为：45.

【点睛】

本题考查该样本的众数的概念，茎叶图的应用，考查了学生的识图能力，属于基础题.

15．

【解析】

【分析】

【详解】

第一-次没有抽到且第二次没有抽到第三次被抽到的概率是

16．

【解析】

试题分析：由图可知，甲的5次成绩分别是88、89、90、91、92，易知甲的平均分为90.乙的成绩分别是83、83、87、99，其中被污损的那次成绩为90到99中的某一个.设被污损的那次成绩为，由甲的平均成绩超过乙的平均成绩，得.所以.又是90到99的十个整数中的其中一个，其中有8个整数小于98，所以的概率.

考点：茎叶图、随机事件的概率

17．（1）0.3；（2）90；（3）71

【解析】

【分析】

（1）根据频率之和为1可得小矩形面积之和为1，由此可求出答案；

（2）根据“频数=样本容量×频率”可求得答案；

（3）直接根据平均数的计算公式计算即可．

【详解】

解：（1）设分数在内的频率为x.根据频率直方分布，则有

，

解得，

∴分数在内的频率为；

（2）数学成绩大于80分的人数为（人）；

（3）估计本次考试的平均分为．

【点睛】

本题主要考查根据频率分布直方图估计总体的分布，属于基础题．

18．（1）见详解；（2）见详解．

【解析】

【分析】

（1）根据茎叶图的概念及画法，可得结果.

（2）根据（1）通过比较品种A，品种B，数据集中情况，可得平均数大小，通过茎叶图看两个品种的分散程度，可得结果.

【详解】

（1）

(2)结合茎叶图可知：

①品种A的亩产平均数比品种B高；

②品种A的亩产标准差(或方差)比品种B大，

故品种A的亩产稳定性较差．

【点睛】

本题主要考查茎叶图的作法以及通过茎叶图来比较统计量的大小，属基础题.

19．（Ⅰ）3125, （Ⅱ）26, （Ⅲ）

【解析】

【分析】

（Ⅰ）根据所有的频率和为1，求出内径介于的频率，即可求解；

（Ⅱ）由频率分布直方图，即可求解；

（Ⅲ）根据频率分布直方图可判断结果.

【详解】

（Ⅰ）依题意，得内径介于的频率为，

所以所求产品数量为.

前个小矩形的面积，

第个小矩形的高度为.

所以所求中位数为.

（Ⅲ）.

【点睛】

本题考查频率分布直方图、样本的数字特征，考查运算求解能力、推理论证能力以及化归与转化思想，属于基础题.

20．（1）见解析；（2）平均数100，方差为104；（3）不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.

【解析】

【分析】

【详解】

（1）直方图如图，

（2）质量指标值的样本平均数为

.

质量指标值的样本方差为

.

（3）质量指标值不低于95的产品所占比例的估计值为

，

由于该估计值小于0.8，故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.

21．（1），；（2）平均数为（元），方差为；（3）一定要停止，理由见解析

【解析】

【分析】

（1）当天需求量时，当天的利润，当天需求量时，当天的利润，由此能求出当天的利润y关于当天需求量n的函数解析式.

（2）由题意，利用平均数和方差的公式，即可求出这30天的日利润的平均数和方差.

（3）根据该统计数据，一定要停止这种面包的生产.推导出连续10天的日需求量都不超过10个，由此说明一定要停止这种面包的生产.

【详解】

（1）由题意可知，当天需求量时，当天的利润，

当天需求量时，当天的利润.

故当天的利润y关于当天需求量n的函数解析式为:，.

（2）由题意可得：

所以这30天的日利润的平均数为（元），

方差为.

（3）根据该统计数据，一定要停止这种面包的生产.理由如下：

由，

可得，

所以（，，），所以，

由此可以说明连续10天的日需求量都不超过10个，即说明一定要停止这种面包的生产.

【点睛】

本题主要考查了函数解析式、平均数、方差的求法，考查函数性质、平均数、方差公式等基础知识综合应用，考查运算求解能力.

22．（1），70%.（2）平均数为76.2，中位数为76.7

【解析】

【分析】

（1）由各组频率和为1即可求得，再求出的频率即可估计高一年级数学成绩在分的学生所占的百分比；

（2）同一组中的数据以该组区间的中点值作代表，分别乘以对应频率，求和即可得平均数；根据中位数两侧频率和均为0.5，列方程即可求得中位数.

【详解】

（1）由题意，

解得，

则由频率分布直方图可估计高一年级数学成绩分的学生所占的百分比为：.

（2）估计成绩的平均数为，中位数为y，

则

，

由频率分布直方图可知，

则，解得.

所以这50名学生数学成绩的平均数为76.2，中位数约为.

【点睛】

本题考查了频率分布直方图的应用，考查了利用频率分布直方图求数据的中位数和平均数，属于中档题.