高中数学北师大版 (2019)必修 第二册6.1 柱、锥、台的侧面展开与面积备课ppt课件

这是一份高中数学北师大版 (2019)必修 第二册6.1 柱、锥、台的侧面展开与面积备课ppt课件，共60页。PPT课件主要包含了提示长方形，长方形，特别提醒，提示扇形，注意转化，圆柱的表面积为，圆锥的表面积为，圆台的表面积为，简单几何体的侧面积，πrl等内容，欢迎下载使用。

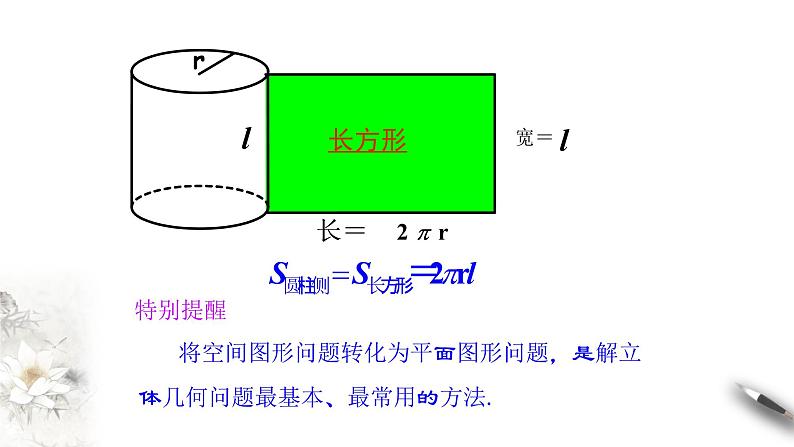
思考1: 把圆柱的侧面沿着一条母线展开，得到什么图形?展开的图形与原图有什么关系？
长方形的面积等于圆柱的侧面积
探究点1 圆柱、圆锥、圆台的侧面积
柱、锥、台的侧面展开与面积
将空间图形问题转化为平面图形问题，是解立体几何问题最基本、最常用的方法.
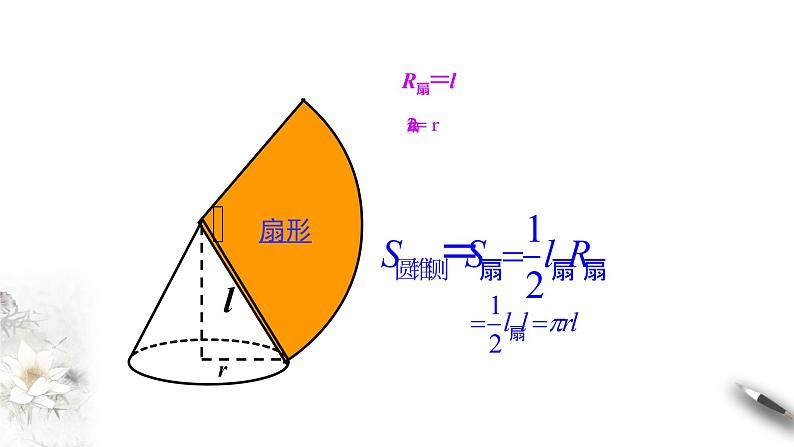
思考2:把圆锥的侧面沿着一条母线展开，得到什么图形?展开的图形与原图有什么关系？
扇形的面积等于圆锥的侧面积
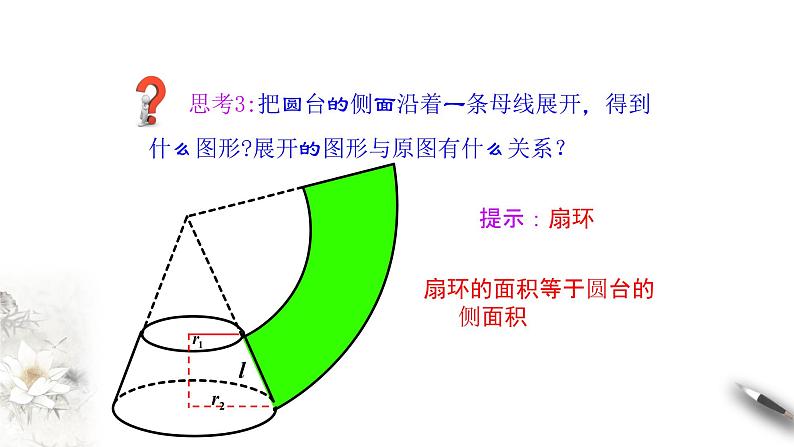
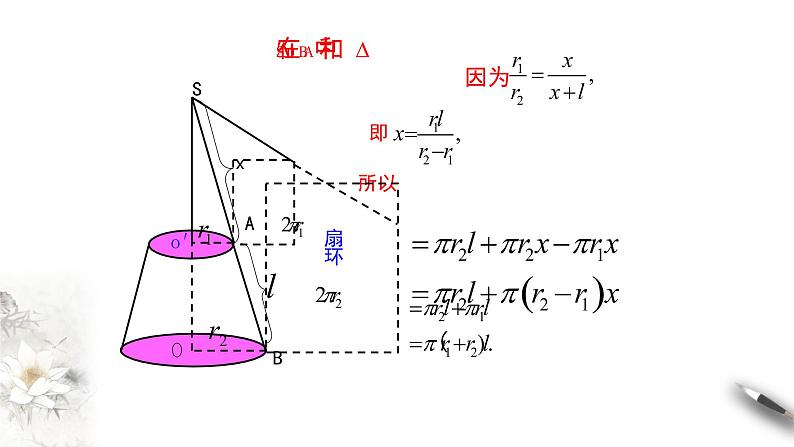
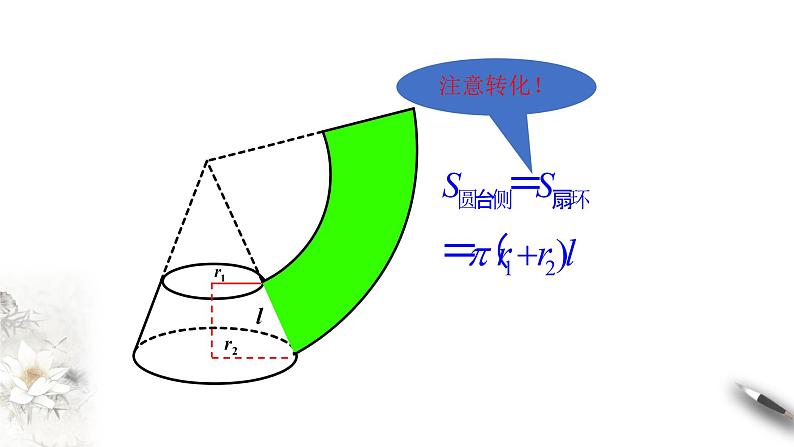
思考3:把圆台的侧面沿着一条母线展开，得到什么图形?展开的图形与原图有什么关系？
提示：扇环
扇环的面积等于圆台的 侧面积
思考4：将圆柱、圆锥、圆台的侧面积公式进行比较，你能发现它们的联系和区别吗？
例1.一个圆柱形的锅炉，底面直径 高 求锅炉的表面积（保留2个有效数字）
例2 圆台的上下底面半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是180°，那么圆台的侧面积是多少？（结果中保留 ）
解 如图，设上底面周长为c,因为扇环的圆心角是180°，所以c= ·SA又因为c=2 ×10=20 ,所以SA=20.同理SB=40.所以，AB=SB-SA=20,S圆台侧=
答：圆台的侧面积为600 cm2
【提升总结】圆柱、圆台、圆锥表面积公式
思考1：把直棱柱、正棱锥、正棱台的侧面分别沿着一条侧棱展开，分别得到什么图形？侧面积是多少？
类比圆柱、圆锥、圆台！
探究点2 直棱柱、正棱锥、正棱台的侧面积
思考2：将直棱柱、正棱锥、正棱台的侧面积公式进行比较,你能发现它们的联系和区别吗？
例3：一个正三棱台的上、下底面边长分别是3cm和6cm，高是3/2cm，求三棱台的侧面积.
分析：关键是求出斜高，注意图中的直角梯形
1．(2014·陕西高考)将边长为1的正方形以其一边所在的直线为旋转轴旋转一周,所得几何体的侧面积是(　　)A.4π B.8π C.2π D.π
2.正四棱锥底面边长为6 ,高是4，中截面把棱锥截成一个小棱锥和一个棱台，则棱台的侧面积为______.
3.一个直角梯形上底、下底和高之比是1:2: ，将此直角梯形以垂直于底的腰所在直线为旋转轴，旋转一周形成一个圆台，则这个圆台上底面积、下底面积和侧面积的比是________.
4. 某几何体的三视图如图所示,该几何体的表面积是_____.
【解析】由三视图可知,原几何体是一个底面是直角梯形,高为4的直四棱柱,其底面积为 28 ,侧面积为64,故表面积为92.
5．一个圆柱的侧面展开图是一个正方形，求这个圆柱的表面积与侧面积的比．
【解析】设底面圆半径为r，母线即高为h．所以h＝2πr．
瞧，多么宏伟壮观的金字塔！你能求出它的体积吗？
看，这不是原来的世贸大厦吗？它们的体积怎么求？
几何体占有空间部分的大小叫做它的体积
几何体的体积是单位体积的多少倍，这个倍数就是这个几何体的体积的数值。
长方体的体积等于它的长、宽、高的积
长方体的体积等于它的底面积s和高h的积
正方体的体积等于它的棱长a 的立方
思考：取一些书堆放在桌面上(如图所示) ，并改变它们的放置方法，观察改变前后的体积是否发生变化？
定理 柱体（棱柱、圆柱）的体积等于它的底 面 积s和高h的积。
类似的,底面积相等,高也相等的两个锥体的体积也相等.
等底面积、等高的锥体间的体积有何关系?
如果一个锥体（棱锥、圆锥）的底面积是Ｓ，高是ｈ，那么它的体积是：
如果圆锥的底面半径是ｒ，高是ｈ，那么它的体积是：　　
Ｖ圆锥＝ πｒ２ｈ
六、圆台的体积：六、圆台的体积：
思考：柱体、锥体、台体的体积公式之间有什么关系？
S为底面积，h为锥体高
S，S'分别为上、下底面面积，h 为台体高
S为底面积，h为柱体高
例1.埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.金字塔高约146.6 m,底面边长约230.4 m. 问这座金字塔的侧面积和体积各是多少?
解:如图,AC为高,BC为底面的边心距,则AC=146.6 m,BC=115.2 m,底面周长 c=4×230.4 m.
答:金字塔的侧面积约是 ,体积约是 .
例2.已知一正四棱台的上底边长为4 cm,下底边长为8 cm,高为3 cm,求其体积.
答：正四棱台的体积为112 cm3.
1.已知一个圆柱底面直径和母线长均为4，则该圆柱的体积为 ( )
C.
2. 一个几何体的三视图如图所示,则该几何体的体积为_______.
【解析】由三视图可知该几何体为一个长方体和一个等高的圆柱的组合体,其中长方体的长、宽、高分别为4、3、1,圆柱的底面直径为2,高为1,所以该几何体的体积为 .
3. 某几何体的三视图如图所示，则该几何体的体积等于__________.
【解析】该几何体是底面是直角梯形，高为4的直四棱柱，则该几何体的体积是V= ×(2+5)×4×4=56.
4.如图，已知正四棱锥P-ABCD的底边长为6、侧棱长为5．求正四棱锥P-ABCD的体积和侧面积．
解：设底面ABCD的中心为O，边BC中点为E， 连接PO，PE，OE. 在Rt△PEB中，PB=5， BE=3，则斜高PE=4. 在Rt△POE中，PE=4，OE=3，则高PO=
柱体、锥体、台体的体积
如果用油漆去涂一个乒乓球和一个篮球，且涂的油漆厚度相同，问哪一个球所用的油漆多？为什么？
只需要求出它们的表面积
一个充满空气的足球和一个充满空气的篮球，球内的气压相同，若忽略球内部材料的厚度，则哪一个球充入的气体较多？为什么？
那如何求球的表面积和体积呢？请进入本节课的学习！
问题2：把直线换成平面，圆换成球，即用一个平面去截球，情况又怎样呢？
问题1：一条直线与圆相交，在圆内的部分是什么图形？提示：弦（线段）.
2.球心到截面的距离d与球的半径R和截面半径r有下面的关系:
1.球心和截面圆心的连线垂直于该截面．
截面：用一个平面去截一个球,截面是圆面(黄色圆面).截面圆：平面截球面所得图形是圆.
1.大圆：球面被经过球心的平面截得的圆叫做大圆.如⊙O(浅蓝色圆面）.
2.小圆：球面被不经过球心的平面截得的圆叫做小圆.如⊙O′(黄色圆面）.
探究点2 球的切线
直线与球相切：当直线与球有唯一交点时，称直线与球相切，其中它们的交点称为直线与球的切点.
问题：过球外一点P，有无数条切线，那么所有切线长都相等吗？所有切点组成什么图形？
提示：如图 ① 可知 ，AP为定值，这说明，过球外一点的所有切线长都相等，这些切点的集合是一个圆.
探究点3 球的表面积和体积
实验：排液法测小球的体积
小球的体积 等于它排开液体的体积
都是以R为自变量的函数
这样可以求出球体体积为
观察球的体积与表面积公式，思考下列问题：思考1:计算球的表面积与体积，关键需要确定哪个量？提示：要计算球的表面积与体积，关键需要确定球的半径R.
思考3.若两球的半径之比为R1∶R2，那么两球的表面积之比及体积之比分别是多少？提示：所以两球的表面积之比为 两球的体积之比为
例1.如图，一个圆锥形的空杯子上面放着一个半球形的冰激凌，如果冰激凌融化了，会溢出杯子吗？（假设冰激凌融化前后体积不变）
所以，冰激凌融化了，不会溢出杯子.
例2.一个圆柱形的玻璃瓶的内半径为3 cm，瓶里所装的水深为8 cm，将一个钢球完全浸入水中，瓶中水的高度上升到8.5 cm，求钢球的半径.
1.填空(1)球的表面积变为原来的2倍,则半径变为原来的 倍.(2)球半径变为原来的2倍，则表面积变为原来的 倍.(3)两球表面积之比为1︰2，则其体积之比是 .(4)两球体积之比是1︰2，则其表面积之比是 .
注意:影响球的表面积及体积的只有一个元素，就是球的半径.
2. 某几何体的三视图如图所示,它的体积为( )A. B. C. D.
【解析】选C.该几何体下部分是半径为3,高为4的圆锥,体积为 ,上部分是半球,体积为 ,所以体积为 .
（2012辽宁理16） 已知正三棱锥 P-ABC，点P，A，B，C都在半径为 的球面上，若PA，PB，PC两两互相垂直，则球心到截面ABC的距离为________.
球的体积和表面积公式已知：球的半径为R.结论：体积V=______， 表面积S=______.