数学1.2 空间几何体的三视图和直观图学案及答案

空间几何体的直观图

学习目标

1、掌握斜二测画法及其步骤；

2、能用斜二测画法画空间几何体的直观图

一、课前准备

学习目标

复习 1：中心投影的投影线            ；平行投影的            ；平行投影又分     投影和    投影

复习 2：物体在正投影下的三视图是      、      、      ；画三视图的要点是       、       、    

引入：空间几何体除了用三视图表示外，更多的是用直观图来表示 用来表示空间图形的平面图叫空间图形的直观图要画空间几何体的直观图，先要学会水平放置的平面图形的画法 我们将学习用斜二测画法来画出它们你知道怎么画吗？

二、新课导学

※ 探索新知

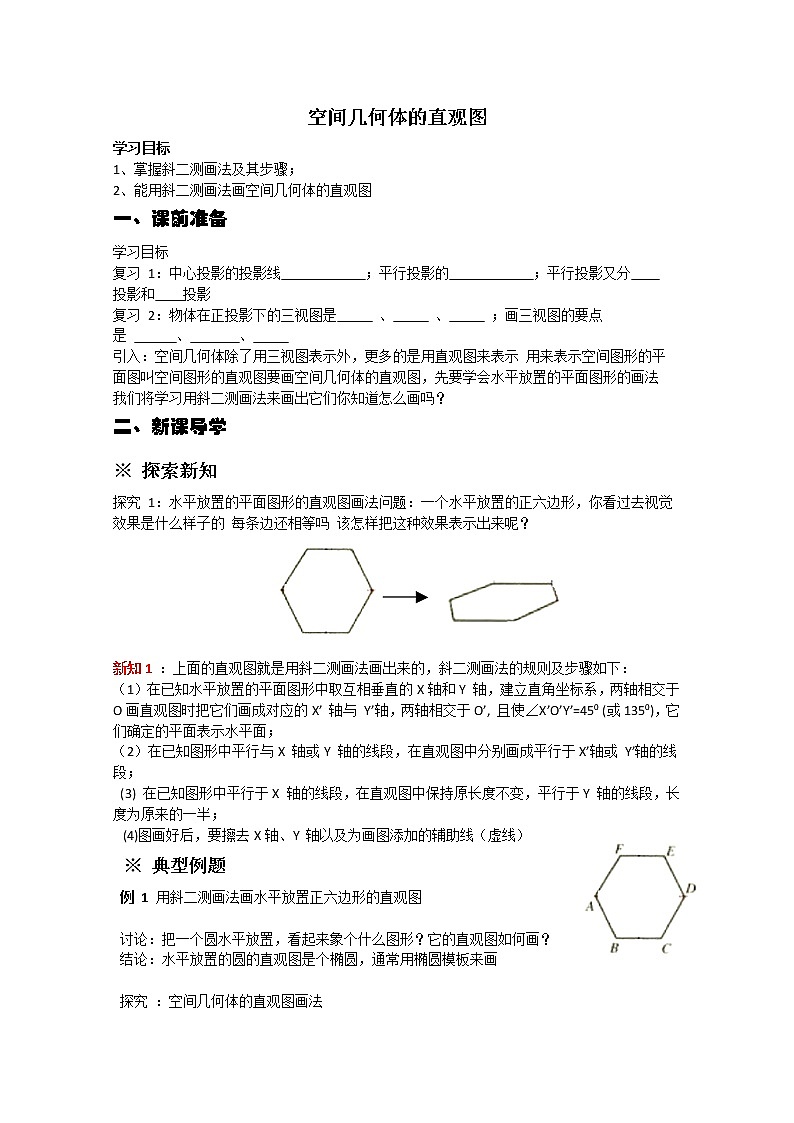
探究 1：水平放置的平面图形的直观图画法问题：一个水平放置的正六边形，你看过去视觉效果是什么样子的 每条边还相等吗 该怎样把这种效果表示出来呢？

新知1 ：上面的直观图就是用斜二测画法画出来的，斜二测画法的规则及步骤如下：

（1）在已知水平放置的平面图形中取互相垂直的X轴和Y 轴，建立直角坐标系，两轴相交于O画直观图时把它们画成对应的X’ 轴与 Y’轴，两轴相交于O’, 且使∠X’O’Y’=450 (或1350)，它们确定的平面表示水平面；

（2）在已知图形中平行与X 轴或Y 轴的线段，在直观图中分别画成平行于X’轴或 Y’轴的线段；

(3) 在已知图形中平行于X 轴的线段，在直观图中保持原长度不变，平行于Y 轴的线段，长度为原来的一半；

(4)图画好后，要擦去X轴、Y 轴以及为画图添加的辅助线（虚线）

※ 典型例题

例 1 用斜二测画法画水平放置正六边形的直观图

讨论：把一个圆水平放置，看起来象个什么图形？它的直观图如何画？

结论：水平放置的圆的直观图是个椭圆，通常用椭圆模板来画

探究 ：空间几何体的直观图画法

问题2：斜二测画法也能画空间几何体的直观图，和平面图形比较，空间几何体多了一个“高 ”，你知道画图时该怎么处理吗？

例 2用斜二测画法画长4cm 、宽3cm 、高2cm 的长方体的直观图

新知2 ：用斜二测画法画空间几何体的直观图时，通常要建立三条轴：X 轴，Y 轴， Z轴；它们相交于点 O，且∠X’O’Y’=450，∠X’O’Z’=900 ；空间几何体的底面作图与水平放置的平面图形作法一样，即图形中平行于X 轴的线段保持长度不变，平行于Y 轴的线段长度为原来的一半，但空间几何体的“高” ，即平行于 Z轴的线段，保持长度不变。

※ 动手试试

练 1用斜二测画法画底面半径为4cm 高为3cm 的圆柱的直观图

例3 如下图，是一个空间几何体的三视图，请用斜二测画法画出它的直观图

练2 由三视图画出物体的直观图.

小结：由简单组合体的三视图画直观图时，先要想象出几何体的形状，它是由哪几个简单几何体怎样构成的；然后由三视图确定这些简单几何体的长度、宽度、高度，再用斜二测画法依次画出来.

三、总结提升

※ 学习小结

1.斜二测画法要点①建坐标系，定水平面；②与坐标轴平行的线段保持平行；③水平线段(X 轴)等长，竖直线段（Y 轴）减半； ④若是空间几何体与X轴平行的线段长度也不变。

2．简单组合体直观图的画法；由三视图画直观图

学习评价

※ 自我评价

你完成本学案的情况为（ ）A很好 B 较好  C一般 D 较差

※ 当堂检测（时量：5分钟 满分：10 分）

1 .一个长方体的长、宽、高分别是4 、8 、4 ，则画其直观图时对应为（ ）

A 4 、8 、4  B 4 、4 、4  C 2 、4 、4  D 2 、4 、2

2利用斜二测画法得到的①三角形的直观图是三角形②平行四边形的直观图是平行四边形③正方形的直观图是正方形④菱形的直观图是菱形，其中正确的是（ ）

A ①②  B①  C③④   D①②③④

3.一个三角形的直观图是腰长4为 的等腰直角三角形，则它的原面积是（ ）

A.8  B.16  C .16 D. 32

4.下图是一个几何体的三视图, 请画出它的图形为                  

5.等腰梯形 ABCD上底边CD=1 ，腰AD=CB=，下底AB=3 ，按平行于上、下底边取X 轴，则直观图A’B’C’D’ 的面积为