高中数学人教版新课标A必修22.1 空间点、直线、平面之间的位置关系课后练习题

这是一份高中数学人教版新课标A必修22.1 空间点、直线、平面之间的位置关系课后练习题，共6页。试卷主要包含了选择题，解答题，填空题等内容，欢迎下载使用。
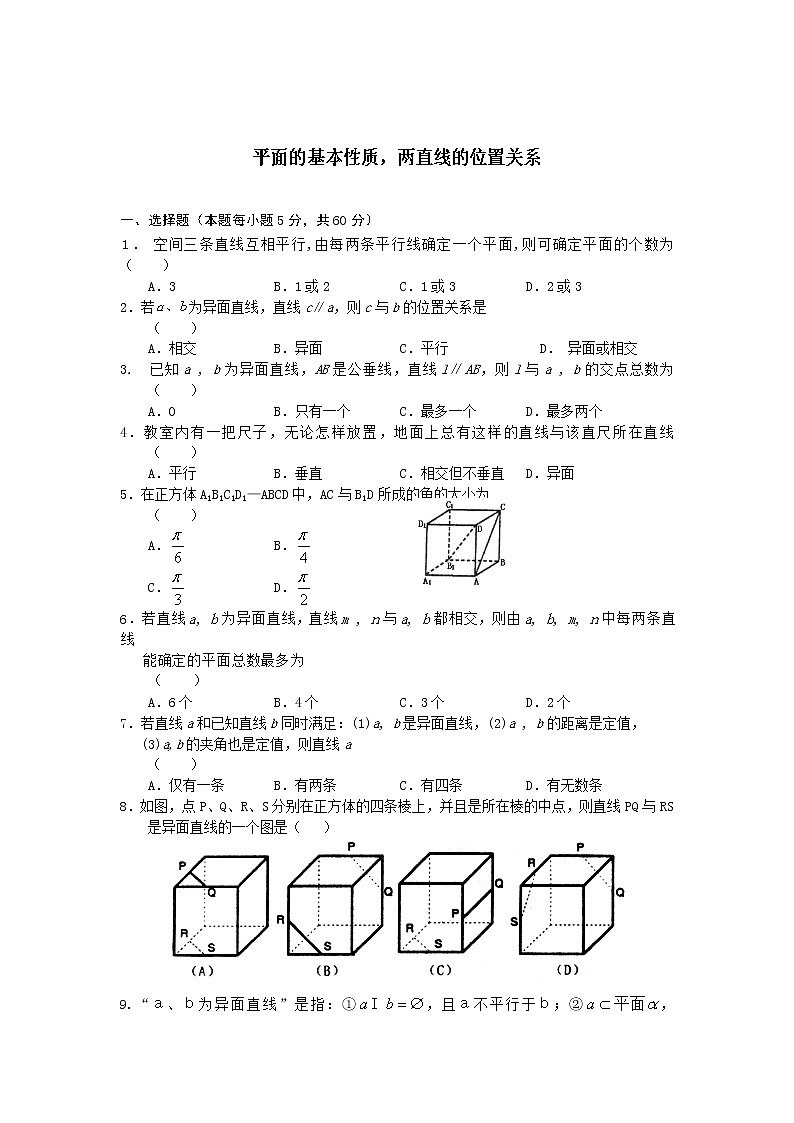
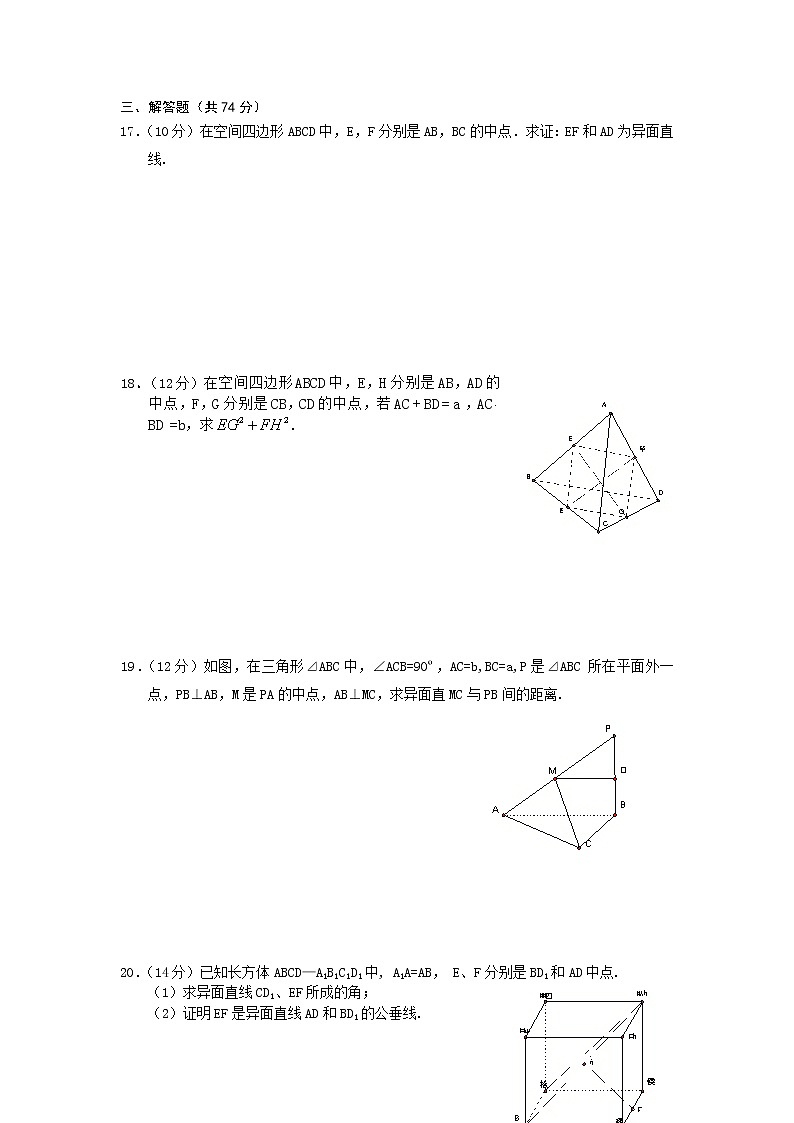
 平面的基本性质，两直线的位置关系 一、选择题（本题每小题5分，共60分）1．空间三条直线互相平行,由每两条平行线确定一个平面,则可确定平面的个数为（    ） A．3 B．1或2 C．1或3 D．2或32．若为异面直线，直线c∥a，则c与b的位置关系是  （    ） A．相交 B．异面 C．平行  D． 异面或相交3.  已知a , b为异面直线，AB是公垂线，直线l∥AB，则l与a , b的交点总数为  （    ）    A．0              B．只有一个       C．最多一个       D．最多两个4．教室内有一把尺子，无论怎样放置，地面上总有这样的直线与该直尺所在直线 （    ）    A．平行    B．垂直    C．相交但不垂直   D．异面5．在正方体A1B1C1D1—ABCD中，AC与B1D所成的角的大小为  （    ）A． B． C． D．6．若直线a, b为异面直线，直线m , n与a, b都相交，则由a, b, m, n中每两条直线   能确定的平面总数最多为   （    ）                                                                   A．6个           B．4个           C．3个            D．2个7．若直线a和已知直线b同时满足：(1)a, b是异面直线，(2)a , b的距离是定值，   (3)a,b的夹角也是定值，则直线a    （    ）    A．仅有一条      B．有两条         C．有四条         D．有无数条8．如图，点P、Q、R、S分别在正方体的四条棱上，并且是所在棱的中点，则直线PQ与RS是异面直线的一个图是（   ）9.“ａ、ｂ为异面直线”是指：①，且ａ不平行于ｂ；②，，且；③，，且；④，；⑤不存在平面能使，. 成立. 其中正确的序号是（　　）Ａ．①④⑤　　 Ｂ．①③④　　 Ｃ．①④　　 Ｄ．①⑤10．如图，是一个无盖正方体盒子的表面展开图，A、B、C为其上的三个点，则在正方体盒子中，∠ABC等于                                                        （    ） A．45°           B．60° C．90°           D．120°  11．线段OA，OB，OC不共面，AOB=BOC=COA=60，OA=1，OB=2，OC=3，则△ABC是     （    ）A．等边三角形  B非等边的等腰三角形C．锐角三角形  D．钝角三角形12．若a，b，l是两两异面的直线，a与b所成的角是，l与a、l与b所成的角都是，则的取值范围是                                                        （    ） A．[] B．[] C．[] D．[]二．填空题（本题每小题4分，共16分）13．小明想利用树影测树高，他在某一时刻测得长为1m的竹竿影长0.9m，但当他马上测树高时, 因树靠近一幢建筑物,影子不全落在地面上，有一部分影子上了墙如图所示.他测得留在地面部分的影子长2.7m, 留在墙壁部分的影高1.2m, 求树高的高度（太阳光线可看作为平行光线）_______.14．如图,正四面体（空间四边形的四条边长及两对角线的长都相等）中,分别是棱的中点, 则和所成的角的大小是________.15．OX，OY，OZ是空间交于同一点O的互相垂直的三条直    线，点P到这三条直线的距离分别为3，4，7，则OP长 为_______.16．设直线a上有6个点，直线b上有9个点，则这15个点，能确定_____个不同的平面. 三、解答题（共74分）17．（10分）在空间四边形ABCD中，E，F分别是AB，BC的中点．求证：EF和AD为异面直线.       18．（12分）在空间四边形ABCD中，E，H分别是AB，AD的中点，F，G分别是CB，CD的中点，若AC + BD = a ，ACBD =b，求.            19．（12分）如图，在三角形⊿ABC中，∠ACB=90º，AC=b,BC=a,P是⊿ABC 所在平面外一点，PB⊥AB，M是PA的中点，AB⊥MC，求异面直MC与PB间的距离.         20．（14分）已知长方体ABCD—A1B1C1D1中, A1A=AB， E、F分别是BD1和AD中点. （1）求异面直线CD1、EF所成的角； （2）证明EF是异面直线AD和BD1的公垂线.       21．（14分） ⊿ABC是边长为2的正三角形，在⊿ABC所在平面外有一点P，PB=PC=，PA=，延长BP至D，使BD=，E是BC的中点，求AE和CD所成角的大小和这两条直线间的距离.     22．（12分）在正方体ABCD—A1B1C1D1中，E，F，G，H，M，N分别是正方体的棱AB，BC，的中点，试证：E，F，G，H，M，N六点共面．        参考答案一、CDCB DBDC DBBD11．解 设 AC=x，AB=y，BC=z，由余弦定理知：x2=12+32-3=7，y2=12+22-2=3，z2=22+32-6=7。∴ △ABC是不等边的等腰三角形，选（B）．12．解 当l与异面直线a，b所成角的平分线平行或重合时，a取得最小值，当l与a、b的公垂线平行时，a取得最大值，故选（D）．二、填空题13．4．2米   解：树高为AB，影长为BE，CD为树留在墙上的影高，CE=米，树影长BE=米，树高AB=BE=米。       14．解：设各棱长为2，则EF=，取AB的中点为M，即15．解：在长方体OXAY—ZBPC中，OX、OY、OZ是相交的三条互相垂直的三条直线。又PZOZ，PYOY，PXOX，有 OX2+OZ2=49，OY2=OX2=9， OY2+OZ2=16，得 OX2+OY2+OZ2=37，OP=．16．解 当直线a，b共面时，可确定一个平面； 当直线a，b异面时，直线a与b上9个点可确定9个不同平面，直线b与a上6个点可确定6个不同平面，所以一点可以确定15个不同的平面．三、解答题17．证明：假设EF和AD在同一平面内，…（2分），则A，B，E，F；……（4分）又A，EAB，∴AB，∴B，……（6分）同理C……（8分）故A，B，C，D，这与ABCD是空间四边形矛盾。∴EF和AD为异面直线．（10分）18．解：四边形EFGH是平行四边形，…………（4分）=2=．．．．．．．（12分）19．解：作MN//AB交PB于点N．（2分）∵PB⊥AB，∴PB⊥MN。（4分）又AB⊥MC，∴MN⊥MC．（8分）MN即为异面直线MC与PB的公垂线段，（10分）其长度就是MC与PB之间的距离， 则得MN=AB=（12分）20．（1）解：∵在平行四边形中，E也是的中点，∴，（2分）∴两相交直线D1C与CD1所成的角即异面直线CD1与EF所成的角.（4分）又A1A=AB，长方体的侧面都是正方形，∴D1CCD1 ∴异面直线CD1、EF所成的角为90°.（7分）（2）证：设AB=AA1=a, ∵D1F=∴EF⊥BD1（9分）由平行四边形，知E也是的中点，且点E是长方体ABCD—A1B1C1D1的对称中心，（12分）∴EA=ED，∴EF⊥AD，又EF⊥BD1，∴EF是异面直线BD1与AD的公垂线.（14分）21．解：分别连接PE和CD，可证PE//CD，（2分）则∠PEA即是AE和CD所成角．（4分）在Rt⊿PBE中，PB=，BE=1，∴PE=。在⊿AEP中，AE=，=．∴∠AEP=60º，即AE和CD所成角是60º．（7分）∵AE⊥BC，PE⊥BC，PE//DC，∴CD⊥BC，∴CE为异面直线AE和CD的公垂线段，（12分）它们之间的距离为1．（14分）22．证明：∵EN//MF，∴EN与MF 共面，（2分）又∵EF//MH，∴EF和MH共面．（4分）∵不共线的三点E，F，M确定一个平面，（6分）∴平面与重合，∴点H。（8分）同理点G．（10分）故E，F，G，H，M，N六点共面．（12分）