吉林省长春市农安县2021-2022学年七年级上学期期末数学试卷（Word版含答案）

这是一份吉林省长春市农安县2021-2022学年七年级上学期期末数学试卷（Word版含答案），共18页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题（每小题3分，共30分）
1．下列说法正确的个数为（ ）
①0是整数；
②﹣0.2是负分数；
③3.2不是正数；
④自然数一定是正数．
A．1B．2C．3D．4
2．下列计算错误的是（ ）
A．﹣2﹣（﹣2）＝0B．﹣3﹣4﹣5＝﹣12
C．﹣7﹣（﹣3）＝﹣10D．3﹣15＝﹣12
3．下列各组中，不是同类项的是（ ）
A．52与25B．﹣ab与ba
C．0.2a2b与﹣a2bD．a2b3与﹣a3b2
4．﹣5的相反数是（ ）
A．B．5C．﹣D．﹣5
5．在有理数﹣32，3.5，﹣（﹣3），|﹣2|、（﹣）2，﹣3.1415926中，负数的个数是（ ）
A．1个B．2个C．3个D．4个
6．根据世界卫生组织的统计，截止10月28日，全球新冠确诊病例累计超过4430万，用科学记数法表示这一数据是（ ）
A．4.43×107B．0.443×108C．44.3×106D．4.43×108
7．下列各组数中，相等的一组是（ ）
A．（﹣2）3与﹣23B．（﹣2）2与﹣22
C．（﹣3×2）3与3×（﹣2）3D．﹣32与（﹣3）+（﹣3）
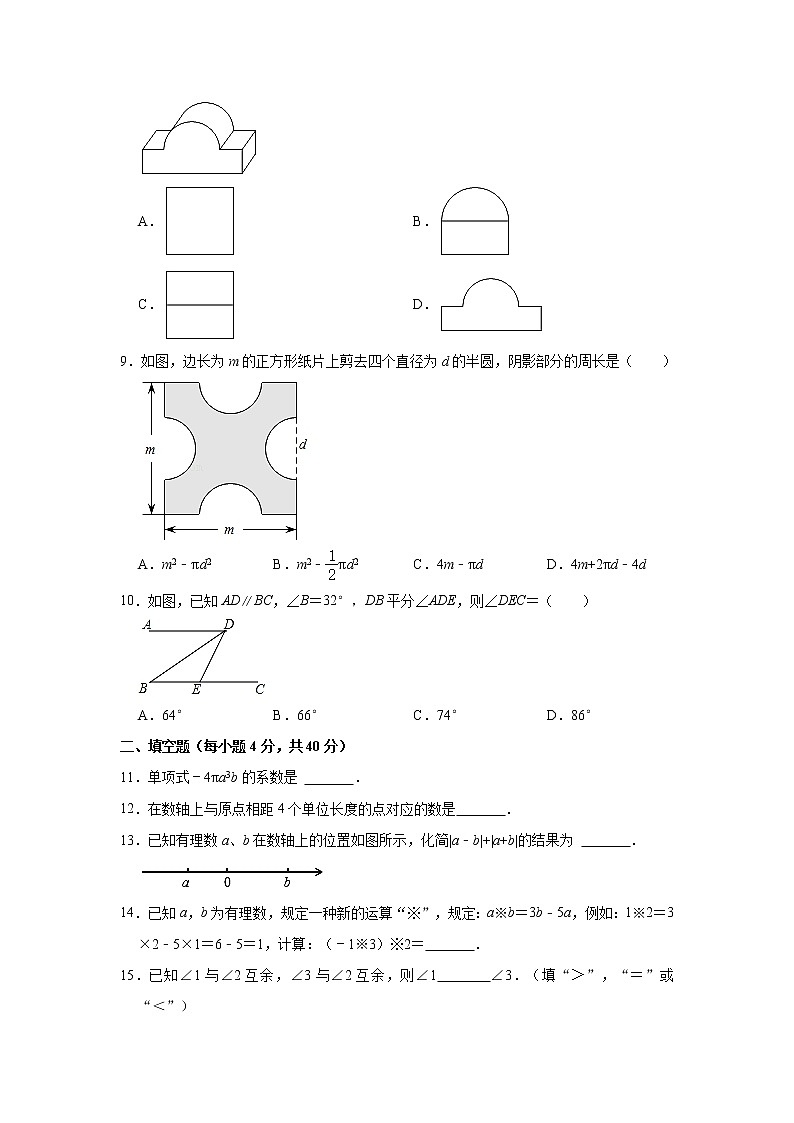
8．如图所示几何体的左视图是（ ）
A．B．
C．D．
9．如图，边长为m的正方形纸片上剪去四个直径为d的半圆，阴影部分的周长是（ ）
A．m2﹣πd2B．m2﹣πd2C．4m﹣πdD．4m+2πd﹣4d
10．如图，已知AD∥BC，∠B＝32°，DB平分∠ADE，则∠DEC＝（ ）
A．64°B．66°C．74°D．86°
二、填空题（每小题4分，共40分）
11．单项式﹣4πa3b的系数是 ．
12．在数轴上与原点相距4个单位长度的点对应的数是 ．
13．已知有理数a、b在数轴上的位置如图所示，化简|a﹣b|+|a+b|的结果为 ．
14．已知a，b为有理数，规定一种新的运算“※”，规定：a※b＝3b﹣5a，例如：1※2＝3×2﹣5×1＝6﹣5＝1，计算：（﹣1※3）※2＝ ．
15．已知∠1与∠2互余，∠3与∠2互余，则∠1 ∠3．（填“＞”，“＝”或“＜”）
16．如图所示，∠AOC与∠BOD都是直角，且∠AOB：∠AOD＝2：11，则∠AOB＝ ．
17．若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和相等，则a+b+c的值为 ．
18．过平面上A，B，C三点中的任意两点作直线，可作 条．
19．废纸回收能减少树木的砍伐量，保持森林覆盖率，有利于封山育林减少水土流失，有利于生态环境，能减少化学原料的运用与排放，减少污染，有利于环境维护和降低消费本钱．若回收废纸1kg，可生产再生纸0.6kg，小明和小亮每学期分别能回收讲义等废纸akg，bkg，这些废纸可生产再生纸 kg．（结果用含a，b的代数式表示）
20．1根1米长的木棒，第一次截去一半，第二次截去剩下的一半，…，如此截下去，则第8次剩下的木棒的长为 米．
三、解答题（21-24题各5分，25、26题各7分，27、28题各8分，共50分）
21．计算：（﹣3）+12+（﹣17）+（+8）．
22．先化简，再求值：5a2﹣[a2﹣（2a﹣5a2）﹣2（a2﹣3a）]，其中a＝4．
23．有理数a，b，c在数轴上的位置如图所示，且|a|＝|b|，化简|c﹣a|+|c﹣b|+|a+b|．
24．如图，O是直线AB上一点，∠AOC＝53°17′，求∠BOC的度数．
25．如图，已知∠ABC＝180°﹣∠A，BD⊥CD于D，EF⊥CD于E．
（1）求证：AD∥BC；
（2）若∠ADB＝36°，求∠EFC的度数．
26．如图，点P是∠AOB的边OB上的一点，过点P画OB的垂线，交OA于点C；
（1）过点P画OA的垂线，垂足为H；
（2）线段PH的长度是点P到 的距离， 是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是 （用“＜”号连接）
27．新学期，两摞规格相同的数学课本整齐的叠放在讲台上，请根据图中所给出的数据信息，解答下列问题：
（1）每本书的高度为 cm，课桌的高度为 cm；
（2）当课本数为x（本）时，请写出同样叠放在桌面上的一摞数学课本高出地面的距离 （用含x的代数式表示）；
（3）桌面上有55本与题（1）中相同的数学课本，整齐叠放成一摞，若有18名同学各从中取走1本，求余下的数学课本高出地面的距离．
28．已知直线AB∥CD，P为平面内一点，连接PA、PD．
（1）如图1，已知∠A＝50°，∠D＝150°，求∠APD的度数；
（2）如图2，判断∠PAB、∠CDP、∠APD之间的数量关系为 ．
（3）如图3，在（2）的条件下，AP⊥PD，DN平分∠PDC，若∠PAN+∠PAB＝∠APD，求∠AND的度数．
参考答案
一、单选题（每小题3分，共30分）
1．下列说法正确的个数为（ ）
①0是整数；
②﹣0.2是负分数；
③3.2不是正数；
④自然数一定是正数．
A．1B．2C．3D．4
【分析】按照实数分类逐个判断即可．
解：∵0为整数，故①正确；
∵﹣0.2为负分数，故②正确；
∵3.2＞0，
∴3.2为正数，故③错误；
∵自然数里面包括0，但0不是正数，故④错误．
故正确的有：①②．
故选：B．
2．下列计算错误的是（ ）
A．﹣2﹣（﹣2）＝0B．﹣3﹣4﹣5＝﹣12
C．﹣7﹣（﹣3）＝﹣10D．3﹣15＝﹣12
【分析】根据有理数的减法运算法则对各选项分析判断后利用排除法求解．
解：A、﹣2﹣（﹣2）＝﹣2+2＝0正确，故本选项错误；
B、﹣3﹣4﹣5＝﹣12正确，故本选项错误；
C、﹣7﹣（﹣3）＝﹣7+3＝﹣4，故本选项正确；
D、3﹣15＝﹣12正确，故本选项错误．
故选：C．
3．下列各组中，不是同类项的是（ ）
A．52与25B．﹣ab与ba
C．0.2a2b与﹣a2bD．a2b3与﹣a3b2
【分析】根据同类项的定义（所含字母相同，并且相同字母的指数也相同，这样的项叫做同类项）即可作出判断．
解：A．52与25是同类项，故此选项不符合题意；
B．﹣ab与ba所含字母相同，相同字母的指数相同，是同类项，故此选项不符合题意；
C．0.2a2b与﹣a2b所含字母相同，相同字母的指数相同，是同类项，故此选项不符合题意；
Da2b3与﹣a3b2所含字母相同，但相同字母的指数不同，不是同类项，故此选项符合题意．
故选：D．
4．﹣5的相反数是（ ）
A．B．5C．﹣D．﹣5
【分析】根据一个数的相反数就是在这个数前面添上“﹣”号，求解即可．
解：﹣5的相反数是5，
故选：B．
5．在有理数﹣32，3.5，﹣（﹣3），|﹣2|、（﹣）2，﹣3.1415926中，负数的个数是（ ）
A．1个B．2个C．3个D．4个
【分析】根据有理数的乘方法则、相反数的概念、绝对值的性质计算，根据负数的概念判断即可．
解：﹣32＝﹣9，﹣（﹣3）＝3，|﹣2|＝2，，
∴﹣32，﹣3.1415926是负数，一共2个，
故选：B．
6．根据世界卫生组织的统计，截止10月28日，全球新冠确诊病例累计超过4430万，用科学记数法表示这一数据是（ ）
A．4.43×107B．0.443×108C．44.3×106D．4.43×108
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
解：4430万＝44300000＝4.43×107．
故选：A．
7．下列各组数中，相等的一组是（ ）
A．（﹣2）3与﹣23B．（﹣2）2与﹣22
C．（﹣3×2）3与3×（﹣2）3D．﹣32与（﹣3）+（﹣3）
【分析】根据乘方的定义和有理数混合运算顺序逐一计算即可判断．
解：A．（﹣2）3＝﹣8，﹣23＝﹣8，相等，此选项符合题意；
B．（﹣2）2＝4，﹣22＝﹣4，不相等，此选项不符合题意；
C．（﹣3×2）3＝（﹣6）3＝﹣216，3×（﹣2）3＝3×（﹣27）＝﹣81，不相等，此选项不符合题意；
D．﹣32＝﹣9，（﹣3）+（﹣3）＝﹣6，不相等，此选项不符合题意；
故选：A．
8．如图所示几何体的左视图是（ ）
A．B．
C．D．
【分析】根据左视图是从左面看到的图形判定则可．
解：从左边看，是一列两个矩形．
故选：C．
9．如图，边长为m的正方形纸片上剪去四个直径为d的半圆，阴影部分的周长是（ ）
A．m2﹣πd2B．m2﹣πd2C．4m﹣πdD．4m+2πd﹣4d
【分析】阴影部分周长为正方形周长加上两个直径为d的圆的周长，再减去四个半圆的直径，从而列式即可．
解：由题意，阴影部分周长为4m+2πd﹣4d，
故选：D．
10．如图，已知AD∥BC，∠B＝32°，DB平分∠ADE，则∠DEC＝（ ）
A．64°B．66°C．74°D．86°
【分析】由AD∥BC，∠B＝32°，根据平行线的性质，可得∠ADB＝32°，又由DB平分∠ADE，可求得∠ADE的度数，继而求得答案．
解：∵AD∥BC，∠B＝32°，
∴∠ADB＝∠B＝32°，
∵DB平分∠ADE，
∴∠ADE＝2∠ADB＝64°，
∵AD∥BC，
∴∠DEC＝∠ADE＝64°．
故选：A．
二、填空题（每小题4分，共40分）
11．单项式﹣4πa3b的系数是 ﹣4π ．
【分析】直接利用单项式的系数确定方法，进而得出答案．
解：单项式﹣4πa3b的系数是：﹣4π．
故答案为：﹣4π．
12．在数轴上与原点相距4个单位长度的点对应的数是 ±4 ．
【分析】分点在原点左边和右边两种情况讨论求解．
解：点在原点左边时，为﹣4，
点在原点右边时，为4，
所以，在数轴上与原点相距4个单位长度的点对应的数是±4．
故答案为：±4．
13．已知有理数a、b在数轴上的位置如图所示，化简|a﹣b|+|a+b|的结果为 2b ．
【分析】观察a、b在数轴上的位置，判断a﹣b与a+b的正负后，再化简．
解：由数轴知：b＞0，a＜0，|b|＞|a|
∴a﹣b＜0，a+b＞0．
∴|a﹣b|+|a+b|
＝﹣（a﹣b）+（a+b）
＝﹣a+b+a+b
＝2b．
故答案为：2b．
14．已知a，b为有理数，规定一种新的运算“※”，规定：a※b＝3b﹣5a，例如：1※2＝3×2﹣5×1＝6﹣5＝1，计算：（﹣1※3）※2＝ 26 ．
【分析】原式利用新定义计算即可得到结果．注意运算顺序．
解：∵a※b＝3b﹣5a，
∴（﹣1※3）※2
＝[﹣（3×3﹣5×1）]※2
＝[﹣（9﹣5）]※2
＝（﹣4））※2
＝3×2﹣5×（﹣4）
＝6+20
＝26．
故答案为：26．
15．已知∠1与∠2互余，∠3与∠2互余，则∠1 ＝ ∠3．（填“＞”，“＝”或“＜”）
【分析】根据余角的性质求解即可．
解：∵∠1与∠2互余，∠3与∠2互余，
∴∠1＝∠3．
故答案为：＝．
16．如图所示，∠AOC与∠BOD都是直角，且∠AOB：∠AOD＝2：11，则∠AOB＝ 20° ．
【分析】由∠AOB+∠BOC＝∠BOC+∠COD知∠AOB＝∠COD，设∠AOB＝2α，则∠AOD＝11α，故∠AOB+∠BOC＝5α＝90°，解得α，从而可求解．
解：∵∠AOB+∠BOC＝∠BOC+∠COD，
∴∠AOB＝∠COD，
设∠AOB＝2α，
∵∠AOB：∠AOD＝2：11，
∴∠AOB+∠BOC＝9α＝90°，
解得α＝10°，
∴∠AOB＝20°．
故答案为：20°．
17．若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和相等，则a+b+c的值为 12 ．
【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点即可得出a+b+c的值．
解：正方体的表面展开图，相对的面之间一定相隔一个正方形，
∴a与b相对，c与﹣2相对，3与2相对，
∵相对面上两个数之和相等，
∴a+b＝c﹣2＝3+2，
∴a+b＝5，c＝7，
∴a+b+c＝12，
故答案为：12．
18．过平面上A，B，C三点中的任意两点作直线，可作 1或3 条．
【分析】分两种情况讨论①三点共线，②三点不共线，由此可得出答案．
解：①
此时可画一条．
②
此时可画三条直线．
故答案为：1或3．
19．废纸回收能减少树木的砍伐量，保持森林覆盖率，有利于封山育林减少水土流失，有利于生态环境，能减少化学原料的运用与排放，减少污染，有利于环境维护和降低消费本钱．若回收废纸1kg，可生产再生纸0.6kg，小明和小亮每学期分别能回收讲义等废纸akg，bkg，这些废纸可生产再生纸 0.6（a+b） kg．（结果用含a，b的代数式表示）
【分析】首先求出小明和小亮每学期回收废纸多少千克，再乘0.6即可求出这些废纸可生产再生纸的千克数即可．
解：（a+b）×0.6＝0.6（a+b）kg．
答：这些废纸可生产再生纸0.6（a+b）kg．
故答案为：0.6（a+b）．
20．1根1米长的木棒，第一次截去一半，第二次截去剩下的一半，…，如此截下去，则第8次剩下的木棒的长为 米．
【分析】根据有理数的乘方的定义解答即可．
解：第一次截去一半，剩下，
第二次截去剩下的一半，剩下×＝（）2，
如此下去，第8次后剩下的长度是（）8＝．
故答案为：．
三、解答题（21-24题各5分，25、26题各7分，27、28题各8分，共50分）
21．计算：（﹣3）+12+（﹣17）+（+8）．
【分析】先根据数的特点进行分组，再进行运算即可．
解：（﹣3）+12+（﹣17）+（+8）
＝[（﹣3）+（﹣17）]+（12+8）
＝（﹣20）+20
＝0．
22．先化简，再求值：5a2﹣[a2﹣（2a﹣5a2）﹣2（a2﹣3a）]，其中a＝4．
【分析】原式去括号合并得到最简结果，把a的值代入计算即可求出值．
解：原式＝5a2﹣a2+2a﹣5a2+2a2﹣6a
＝a2﹣4a，
当a＝4时，原式＝16﹣16＝0．
23．有理数a，b，c在数轴上的位置如图所示，且|a|＝|b|，化简|c﹣a|+|c﹣b|+|a+b|．
【分析】由数轴可知：b＞c＞0，a＜0，再根据有理数的运算法则，求出绝对值里的代数式的正负性，最后根据绝对值的性质化简．
解：由数轴，得b＞c＞0，a＜0，又|a|＝|b|，
∴c﹣a＞0，c﹣b＜0，a+b＝0．
|c﹣a|+|c﹣b|+|a+b|＝c﹣a+b﹣c＝b﹣a．
24．如图，O是直线AB上一点，∠AOC＝53°17′，求∠BOC的度数．
【分析】根据平角的定义列式计算即可．
解：∵∠AOC+∠BOC＝180°，∠AOC＝53°17′，
∴∠BOC＝180°﹣53°17′
＝179°60′﹣53°17′
＝126°43′．
答：∠BOC的度数为126°43′．
25．如图，已知∠ABC＝180°﹣∠A，BD⊥CD于D，EF⊥CD于E．
（1）求证：AD∥BC；
（2）若∠ADB＝36°，求∠EFC的度数．
【分析】（1）求出∠ABC+∠A＝180°，根据平行线的判定推出即可；
（2）根据平行线的性质求出∠DBC，根据垂直推出BD∥EF，根据平行线的性质即可求出∠EFC．
【解答】（1）证明：∵∠ABC＝180°﹣∠A，
∴∠ABC+∠A＝180°，
∴AD∥BC；
（2）∵AD∥BC，∠ADB＝36°，
∴∠DBC＝∠ADB＝36°，
∵BD⊥CD，EF⊥CD，
∴BD∥EF，
∴∠DBC＝∠EFC＝36°
26．如图，点P是∠AOB的边OB上的一点，过点P画OB的垂线，交OA于点C；
（1）过点P画OA的垂线，垂足为H；
（2）线段PH的长度是点P到 OA 的距离， 线段CP的长度 是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是 PH＜PC＜OC （用“＜”号连接）
【分析】（1）过点P画OA的垂线，即过点P画∠PHO＝90°即可，
（2）利用点到直线的距离可以判断线段PH的长度是点P到OA的距离，PC是点C到直线OB的距离，线段PC、PH、OC这三条线段大小关系是PH＜PC＜OC．
解：（1）如图：
（2）线段PH的长度是点P到直线OA的距离，
线段CP的长度是点C到直线OB的距离，
根据垂线段最短可得：PH＜PC＜OC，
故答案为：OA，线段CP，PH＜PC＜OC．
27．新学期，两摞规格相同的数学课本整齐的叠放在讲台上，请根据图中所给出的数据信息，解答下列问题：
（1）每本书的高度为 0.5 cm，课桌的高度为 85 cm；
（2）当课本数为x（本）时，请写出同样叠放在桌面上的一摞数学课本高出地面的距离 （85+0.5x）cm （用含x的代数式表示）；
（3）桌面上有55本与题（1）中相同的数学课本，整齐叠放成一摞，若有18名同学各从中取走1本，求余下的数学课本高出地面的距离．
【分析】（1）让高摞书距离地面的距离减去低摞书距离地面的距离后除以3即为每本数的高度；让低摞书的高度减去3本书的高度即为课桌的高度；
（2）高出地面的距离＝课桌的高度+x本书的高度，把相关数值代入即可；
（3）把x＝55﹣18代入（2）得到的代数式求值即可．
解：（1）书的厚度为：（88﹣86.5）÷（6﹣3）＝0.5cm；
课桌的高度为：86.5﹣3×0.5＝85cm．
故答案为：0.5；85；
（2）∵x本书的高度为0.5x，课桌的高度为85，
∴高出地面的距离为85+0.5x（cm）．
故答案为：（85+0.5x）cm；
（3）当x＝55﹣18＝37时，85+0.5x＝103.5cm．
故余下的数学课本高出地面的距离是103.5cm．
28．已知直线AB∥CD，P为平面内一点，连接PA、PD．
（1）如图1，已知∠A＝50°，∠D＝150°，求∠APD的度数；
（2）如图2，判断∠PAB、∠CDP、∠APD之间的数量关系为 ∠CDP+∠PAB﹣APD＝180° ．
（3）如图3，在（2）的条件下，AP⊥PD，DN平分∠PDC，若∠PAN+∠PAB＝∠APD，求∠AND的度数．
【分析】（1）过点P作EF∥AB，根据平行线的性质可得∠APE＝∠A＝50°，∠EPD＝180°﹣150°＝30°，即可求出∠APD的度数；
（2）过点P作EF∥AB，则AB∥EF∥CD，根据平行线的性质可得∠CDP＝∠DPF，∠FPA+∠PAB＝180°，又∠FPA＝∠DPF﹣APD，即可得出∠CDP+∠PAB﹣APD＝180°；
（3）PD交AN于点O，由AP⊥PD，得出∠APO＝90°，由∠PAN+∠PAB＝∠APD得出∠PAN+∠PAB＝90°，由∠POA+∠PAN＝90°，得出∠POA＝∠PAB，由对顶角相等得出∠NOD＝∠PAB，由角平分线的性质得出∠ODN＝∠PDC，即∠AND＝180°﹣（∠PAB+∠PDC），由（2）得：∠CDP+∠PAB﹣APD＝180°，代入计算即可求出∠AND的度数．
解：（1）如图1，过点P作EF∥AB，
∵∠A＝50°，
∴∠APE＝∠A＝50°，
∵AB∥CD，
∴EF∥CD，
∴∠CDP+∠EPD＝180°，
∵∠D＝150°，
∴∠EPD＝180°﹣150°＝30°，
∴∠APD＝∠APE+∠EPD＝50°+30°＝80°；
（2）如图2，过点P作EF∥AB，则AB∥EF∥CD，
∴∠CDP＝∠DPF，∠FPA+∠PAB＝180°，
∵∠FPA＝∠DPF﹣APD，
∴∠DPF﹣APD+∠PAB＝180°，
∴∠CDP+∠PAB﹣APD＝180°，
故答案为：∠CDP+∠PAB﹣APD＝180°；
（3）如图3，PD交AN于点O，
∵AP⊥PD，
∴∠APO＝90°，
∵∠PAN+∠PAB＝∠APD，
∴∠PAN+∠PAB＝90°，
∵∠POA+∠PAN＝90°，
∴∠POA＝∠PAB，
∵∠POA＝∠NOD，
∴∠NOD＝∠PAB，
∵DN平分∠PDC，
∴∠ODN＝∠PDC，
∴∠AND＝180°﹣∠NOD﹣∠ODN
＝180°﹣（∠PAB+∠PDC），
由（2）得：∠CDP+∠PAB﹣APD＝180°，
∴∠CDP+∠PAB＝180°+∠APD，
∴∠AND＝180°﹣（∠PAB+∠PDC）
＝180°﹣（180°+∠APD）
＝180°﹣（180°+90°）
＝45°．