第8章数学建模活动（一）基础测试-【新教材】北师大版（2019）高中数学必修第一册期末复习

这是一份第8章数学建模活动（一）基础测试-【新教材】北师大版（2019）高中数学必修第一册期末复习，共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
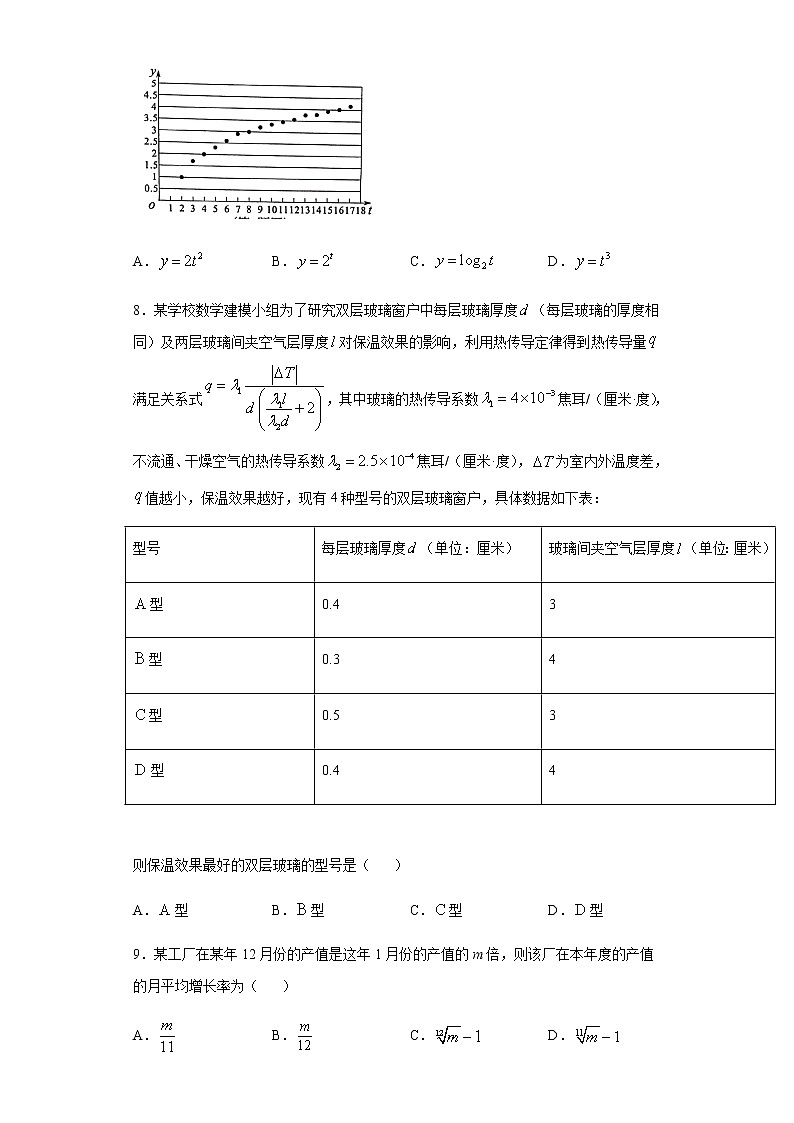
北师大新版数学必修第一册第八章数学建模活动（一）基础测试题  一、单选题1．某公司在甲、乙两地销售一种品牌车,利润（单位：万元）分别为L1=5.06x－0.15 x 2和L2=2x，其中x为销售量（单位：辆）.若该公司在这两地共销售15辆车，则能获得的最大利润为A．45.606 B．45.6 C．45.56 D．45.512．一种产品的成本是a元．今后m（m∈N*）年内，计划使成本平均每年比上一年降低p%，成本y是经过年数x的函数（0<x<m，且x∈N*），其关系式为A．y=a（1+p%）x B．y=a（1–p%）x C．y=a（p%）x D．y=a–（p%）x3．某自行车存车处在某一天总共存放车辆4 000辆次，存车费为：电动自行车1元/辆，普通自行车0.5元/辆．若该天普通自行车存车x辆次，存车费总收入为y元，则y与x的函数关系式为（  ）A．y＝0.5x（0≤x≤4 000） B．y＝1.5x（0≤x≤4 000）C．y＝－0.5x＋4 000（0≤x≤4 000） D．y＝0.5x＋4 000（0≤x≤4 000）4．    某自行车存车处在某一天总共存放车辆4 000辆次，存车费为：电动自行车0.3元/辆，普通自行车0.2元/辆．若该天普通自行车存车x辆次，存车费总收入为y元，则y与x的函数关系式为(　　)A．y＝0.2x(0≤x≤4 000)B．y＝0.5x(0≤x≤4 000)C．y＝－0.1x＋1 200(0≤x≤4 000)D．y＝0.1x＋1 200(0≤x≤4 000)5．据你估计，一种商品在销售收入不变的条件下，其销量与价格之间的关系最可能是下图中的（    ）A． B． C． D．6．“依法纳税是每个公民应尽的义务”，国家征收个人所得税是分段计算的，总收入不超过元，免征个人所得税，超过元部分需征税，设全月纳税所得额为，全月总收入元，税率见下表：级数全月纳税所得额税率不超过元部分超过元至元部分超过元至元部分………超过元部分 某人一月份应缴纳此项税款元，则他当月工资总收入介于（）A．元 B．元C．元 D．元7．某研究小组在一项实验中获得一组关于之间的数据，将其整理得到如图所示的散点图，下列函数中最能近似刻画与之间关系的是（   ）A． B． C． D．8．某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度（每层玻璃的厚度相同）及两层玻璃间夹空气层厚度对保温效果的影响，利用热传导定律得到热传导量满足关系式，其中玻璃的热传导系数焦耳/（厘米·度），不流通、干燥空气的热传导系数焦耳/（厘米·度），为室内外温度差，值越小，保温效果越好，现有4种型号的双层玻璃窗户，具体数据如下表：型号每层玻璃厚度（单位：厘米）玻璃间夹空气层厚度（单位：厘米）型0.43型0.34型0.53型0.44 则保温效果最好的双层玻璃的型号是（    ）A．型 B．型 C．型 D．型9．某工厂在某年12月份的产值是这年1月份的产值的m倍，则该厂在本年度的产值的月平均增长率为（    ）A． B． C． D．10．为了保护水资源，提倡节约用水，某城市对居民生活用水实行“阶梯水价”，计费方法如下：每户每月用水量水价不超过12m3的部分3元/m3超过12m3但不超过18m3的部分6元/m3超过18m3的部分9元/m3 若某户居民本月交纳的水费为54元，则此户居民本月用水量为（    ）A．20m3 B．18m3C．15m3 D．14m311．如图是我国2008年—2017年年增量统计图．下列说法正确的是（   ）A．2009年比2008年少B．与上一年比，年增量的增量最大的是2017年C．从2011年到2015年，年增量逐年减少D．2016年年增长率比2012年年增长率小12．图甲中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律、对捕食者和被捕食者数量之间的关系描述错误的是（   ）A．捕食者和被捕食者数量与时间以年为周期B．由图可知，当捕食者数量增多的过程中，被捕食者数量先增多后减少C．捕食者和被捕食者数量之间的关系可以用图1乙描述D．捕食者的数量在第年和年之间数量在急速减少  二、填空题13．2011年9月1日起，我国实行新个人所得税率，起征点为3500元，超过部分实行超额累进税率.如果月工资20000元，则应交税为__________元.应纳锐收入（元）税率（%）不超过1500元3超过1500元至4500元10超过4500元至9000元20超过9000元至35000元25  14．建造一个容积为8m3、深为2m的长方体形状的无盖水池，已知池底和池壁的造价 别为100元/m2和60元/m2，总造价y (单位：元）关于底面一边长x (单位：m)的函数解析式为_______．15．某公司一年需要购买某种原材料400吨，计划每次购买吨，已知每次的运费为4万元/次，一年总的库存费用为万元，为了使总的费用最低，每次购买的数量为 _____________ ；16．大西洋鲑鱼每年都要逆流而上，游回产地产卵.研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数，单位是，其中表示鱼的耗氧量的单位数.当一条鱼的耗氧量是2700个单位时，它的游速是______. 三、解答题17．工厂生产某种产品，次品率p与日产量x(万件)间的关系为: (c为常数， 且0<c<6).已知每生产1件合格产品盈利3元，每出现1件次品亏损1.5元.（1）将日盈利额y(万元)表示为日产量x(万件)的函数；（2）为使日盈利额最大，日产量应为多少万件？18．为保护环境，某单位采用新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最多不超过300吨，月处理成本（元）与月处理量（吨）之间的函数关系式可近似的表示为：，且每处理一吨二氧化碳得到可利用的化工产品价值为300元．（1）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？（2）要保证该单位每月不亏损，则每月处理量应控制在什么范围？19．甲、乙两城相距100，在两城之间距甲城处的丙地建一核电站给甲、乙两城供电，为保证城市安全，核电站距两地的距离不少于10．已知各城供电费用（元）与供电距离（）的平方和供电量（亿千瓦时）之积都成正比，比例系数均是=0．25，若甲城供电量为20亿千瓦时/月，乙城供电量为10亿千瓦时/月，（1）把月供电总费用（元）表示成（）的函数，并求其定义域；（2）求核电站建在距甲城多远处，才能使月供电总费用最小．20．20世纪70年代，里克特制订了一种表明地震能量大小的尺度，就是使用测震仪衡量地震能量的等级，地震能量越大，测震仪记录的地震曲线的振幅就越大，这就是我们常说的里氏震级M，其计算公式为：M＝lg A－lg A0．其中A是被测地震的最大振幅，A0是“标准地震”的振幅．（1）假设在一次地震中，一个距离震中1 000千米的测震仪记录的地震最大振幅是20，此时标准地震的振幅是0.002，计算这次地震的震级；（2）5级地震给人的震感已比较明显，我国发生在汶川的8级地震的最大振幅是5级地震的最大振幅的多少倍？21．某企业生产一种机器的固定成本（即固定投入）为0.5万元，但每生产1百台时又需可变成本（即需另增加投入）0.25万元，市场对此商品的需求量为5百台，销售收入（单位：万元）的函数为，其中x是产品生产并售出的数量（单位：百台）．（1）把利润表示为年产量的函数．（2）年产量为多少时，企业所得利润最大？（3）年产量为多少时，企业才不亏本（不赔钱）？22．有研究表明，声音在空气中的传播速度与空气的温度有关，当空气的温度变化，声音的传播速度也将随着变化．声音在空气中传播速度与空气温度关系一些数据（如下表格）温度…﹣20﹣100102030…声速…318324330336342348…  （1）指出在这个变化过程中的自变量和因变量；（2）当声音在空气中传播速度为342m/s时，此时空气的温度是多少？（3）该数据表明：空气的温度每升高，声音的传播速度将增大（或减少）多少？（4）用表示声音在空气中的传播速度，表示空气温度，根据（3）中你发现的规律，直接写出与之间的关系式．
参考答案1．B【解析】主要考查构建函数模型，利用导数解决生活中的优化问题．解：设甲地销售辆，依题意L1 +L2=5.06－0.15 +2（15－）==，所以当取整数10时，最大利润为45.6，故选B．2．B【分析】根据题意，成本每年降低率相同，符合指数函数模型问题，利用指数函数即可解决问题【详解】根据题意，得y=a（1–p%）x，∵x是年数，又由题意0<x<m，x∈N，因此所求关系式为y=a（1–p%）x（x∈N，1<x<m）．故选B．【点睛】本题考查了指数函数模型的应用问题，解题时应根据题意，建设指数函数模型，从而解决问题，是基础题3．C【分析】普通自行车存车费为,电动自行车存车费用为，两项相加即得．【详解】由题意，若该天普通自行车存车辆次，则该天电动自行车存车4 000－辆次，所以得y＝1×（4 000－x）＋0.5x＝－0.5x＋4 000．故选C．【点睛】本题考查了函数的应用，属基础题．4．C【解析】由题意知，普通自行车存车x辆时，电动自行车存车4000-x辆，则, 0≤x≤4 000故选C5．C【分析】先求得销售量关于价格的函数关系式，由此判断出正确选项.【详解】∵销售收入不变，∴不妨设（定值），∴为反比例函数.故选C.【点睛】本小题主要考查根据题目条件求函数关系式，考查反比例函数图像的识别，属于基础题.6．C【分析】根据表格数据可计算得到超过元的工资收入为元，从而计算得到当月工资.【详解】，又，即超过元的部分为元当月工资为：元本题正确选项：【点睛】本题考查函数模型的实际应用问题，属于基础题.7．C【分析】根据图中的特殊点（2,1），（4,2）即可得解.【详解】根据图中的特殊点（2,1），（4,2）,通过选项可知只有C：满足题意.故选C.【点睛】本题考查了由函数图象写解析式，可以进行选项验证，属于基础题.8．D【分析】依题意可得，所以转化为求的最大值即可得到答案.【详解】，固定，可知最大时，最小，保温效果最好，对于型玻璃，，对于型玻璃，，对于型玻璃，，对于型玻璃，，经过比较可知， 型玻璃保温效果最好.故选：D.【点睛】本题考查了函数的应用，考查了求函数的最值，属于基础题.9．D【分析】先假设增长率为，再根据条件可得，从而可解．【详解】由题意，该厂去年产值的月平均增长率为，则.解得：故选：D．【点睛】本题考查函数模型的选择，利用了有关增长率问题的函数模型，属于基础题．10．C【分析】利用分段函数各段上的解析式,由函数值求自变量可得.【详解】设此户居民本月用水量为,缴纳的水费为元,则当时,元,不符合题意;当时,,令,解得,符合题意;当时,,不符合题意.综上所述: 此户居民本月用水量为15.故选:C【点睛】本题考查了分段函数由函数值求自变量,解题关键是仔细阅读,搞清题意,本题属于基础题.11．D【详解】对于选项，2009年比2008年多29565亿元，故错误，对于选项，由增量图可知：与上一年比，年增量的增量最大的是2010年，故错误，对于选项，从2011年到2015年，除2013年外，年增量逐年减少，故错误，对于选项，因为增长率等于增长量除以上一年产量值，由于上一年产值不确定，所以2016年的产值年增长率可能比2012年的产值年增长率低，故正确．故选：．12．C【解析】分析：由题意可知：捕食者和被捕食者数量与时间以10年为周期呈周期性变化，故捕食者和被捕食者数量之间的关系应为环状，进而得到答案详解：由已知中某理想状态下捕食者和被捕食者数量随时间的变化规律．可得捕食者和被捕食者数量与时间以10年为周期呈周期性变化，捕食者的数量在第25年和30年之间数量在急速减少，正确；由图可知，当捕食者数量增多的过程中，被捕食者数量先增多后减少，故捕食者和被捕食者数量之间的关系应为环状，捕食者和被捕食者数量之间的关系可以用图1乙描述，显然不正确；故选C．点睛：本题考查的知识点是函数的图象的识别，本题比较抽象，属于中档题．13．【分析】由表格和题意求出月工资元应交的税即可．【详解】由表格得，月工资元， 则应交税为（元）.故答案为：．【点睛】本题考查分段函数的实际应用，属于基础题．14．y＝400＋240(x＋)【分析】由题得池子的底面积为4，所以底面另外一边的长度为，再根据已知写出y的表达式即得解.【详解】由题得池子的底面积为4，所以底面另外一边的长度为，所以总造价为.故答案为y＝400＋240(x＋)【点睛】本题主要考查函数解析式的求法，意在考查学生对这些知识的掌握水平和分析推理能力.15．20吨【分析】依题意写出表达式，均值不等式求最小值．【详解】由题意，总的费用，当时取“=”，所以答案为20吨．【点睛】实际问题一定注意实际问题中自变量的取值，取等号的条件．16．【分析】依据题意,将代入即可得出答案.【详解】当时,,故答案为:.【点睛】本题主要考查对数运算,属于基础题.17．（1）；（2）当时，日产量为万件，当时，日产量为3万件时，日盈利额最大．【分析】（1）由题意日产量为万件时，次品为（万件）正品为（万件），由此可得利润函数；（2）由（1）知要使利润最大，则，把函数进行常数分离，然后根据基本不等式或函数的单调性得出最大值．【详解】（1）当时，，当时，，∴．（2）由（1）知要使利润最大，则，此时，，∵又，∴，若，则，当且仅当时取等号；若，函数在上为单调减函数，时取最大值．∴当时，日产量为万件，当时，日产量为3万件时，日盈利额最大．【点睛】本题考查函数的应用，解题关键是根据题意列出函数关系式．本题中要注意次品率这个概念的理解．18．（1）时，才能使每吨的平均处理成本最低；（2）当时，该单位每月不亏损.【分析】(1) 二氧化碳的每吨平均处理成本为,由均值不等式求得结果；（2）结合二次函数的性质以及题意得到结果.【详解】（1）由题意可知，二氧化碳的每吨平均处理成本为因为，当且仅当，即时，才能使每吨的平均处理成本最低;（2）设该单位每月获利为S（元），则 即 ,由题意可知，所以当时，该单位每月不亏损.【点睛】本题考查函数模型的构建，考查学生的阅读能力，考查解不等式，同时考查基本不等式的运用，建立函数模型是关键．19．（1）（2）【解析】试题分析：（Ⅰ）甲城供电费用y1=0．25×20x2，乙城供电费用y2=0．25×10（100-x）2，总费用y=y1+y2，整理即可；因为核电站距甲城xkm，则距乙城（100-x）km，由x≥10，且100-x≥10，得x的范围；（Ⅱ）因为函数y=7．5x2-500x+25000是二次函数，由二次函数的性质可得，x=-时，函数y取得最小值试题解析：（1）由题意知：经化简，为．定义域为[10,90]--- -5分（2）将（1）中函数配方为，所以当月供电总费用最小，为元．---10分．考点：函数模型的选择与应用；二次函数在闭区间上的最值20．（1）4级；（2）1000倍．【分析】（1）将最大振幅和最小振幅代入 即可求得．（2）将里氏震级和 分别代入 后，两式相减变形即可求得．【详解】（1）M＝lgA－lgA0＝＝＝4．即这次地震的震级为4级．（2），＝3，＝1 000，即我国发生在汶川的8级地震的最大振幅是5级地震的最大振幅的1000倍．【点睛】本题考查了函数的应用，属基础题．21．（1）；（2）475台；（3）年产量在11台到4800台之间时，企业不亏本．【分析】（1）根据利润函数＝销售收入函数−成本函数，由此即可求出结果；（2）由利润函数是二次函数，可以利用二次函数的性质求出函数取最大值时对应的自变量的值；（3）要使企业不亏本，则利润，根据分段函数，分类解不等式，即可求出结果．【详解】（1）设利润为y万元，得即（2）显然当时，企业会获得最大利润，此时，，，即年产量为475台时，企业所得利润最大．（3）要使企业不亏本，则．即或得或，即．即年产量在11台到4800台之间时，企业不亏本．【点睛】本题主要考查了分段函数的应用，属于基础题.22．（1）自变量是温度，因变量是声速；（2）；（3）；（4）．【分析】（1）由题设关于变量的表述可得温度为自变量，声速为因变量；（2）根据表中数据可得传播速度为342m/s时，空气的温度为；（3）根据数据表中的数据可得声音的传播速度将增大；（4）根据散点图可得出与之间的关系为，代入表中两组数据后可求函数关系式.【详解】（1）由题设可得：当空气的温度变化，声音的传播速度也将随着变化．因此自变量是温度，因变量是声速.（2）根据题设中给出的数据表可知：当传播速度为342m/s时，空气的温度为.（3）因为，所以空气的温度每升高，声音的传播速度将增大. （4）数据表对应的散点图如图所示：故与之间的关系为，所以，解得，所以.【点睛】本题考查根据数据寻找拟合函数，还考查了对数据的分析与整理，注意函数形式的确定应依据散点图的形状来确定，本题属于基础题.