小升初数学总复习小升初—图形专题课件PPT

这是一份小升初数学总复习小升初—图形专题课件PPT，共60页。PPT课件主要包含了巧求面积，圆和正方形，分析与解答等内容，欢迎下载使用。
图形的周长面积体积公式
正方形/正方体长方形/长方体三角形平行四边形梯形圆形/扇形圆柱圆锥
　例1 小两个正方形组成下图所示的组合图形。已知组合图形的周长是52厘米，DG=4厘米，求阴影部分的面积。
两个正方形的边长之和等于（52-4）÷3=16（厘米）
大正方形边长=（16+4）÷2=10（厘米）
小正方形边长=（16-4）÷2=6（厘米）
　102+62-（10×10÷2）-（10+6）×6÷2=38（厘米2）。
例2如左下图所示，四边形ABCD与DEFG都是平行四边形，证明它们的面积相等。
平行四边形ABCD的面积是三角形DCE的两倍
四边形DEFG的面积也是三角形DCE的两倍
　两个平行四边形的面积都是三角形DCE的两倍
例3如左下图所示，一个腰长是20厘米的等腰三角形的面积是140厘米2，在底边上任意取一点，这个点到两腰的垂线段的长分别是a厘米和b厘米。求a+b的长。
两个小三角形的面积分别为　　20×a÷2和20×b÷2
20×a÷2+20×b÷2=140
10×（a+b）=140
　a+b=14（厘米）
例4如左下图所示，三角形ABC的面积是10厘米2，将AB，BC，CA分别延长一倍到D，E，F，两两连结D，E，F，得到一个新的三角形DEF。求三角形DEF的面积。
三角形ADF的面积是10+10=20（厘米2）
三角形BDE与三角形CEF的面积都等于20厘米2
三角形DEF的面积等于20×3+10=70（厘米2）
例5一个正方形，将它的一边截去15厘米，另一边截去10厘米，剩下的长方形比原来正方形的面积减少1725厘米2，求剩下的长方形的面积。
（甲+丙）+（乙+丙）　　= 甲+乙+丙）+丙　　= 1725+150　　= 1875（厘米2）
原正方形的的边长等于1875÷25=75（厘米）
长方形的面积等于75×75-1725=3900（厘米2）
例6有红、黄、绿三块同样大小的正方形纸片，放在一个正方形盒的底部，它们之间互相叠合（见右图）。已知露在外面的部分中，红色面积是20，黄色面积是14，绿色面积是10，求正方形盒子底部的面积。
（14+10）÷2=12。　　因为绿：红=A∶黄，所以　　绿×黄=红×A，　　A=绿×黄÷红　　 =12×12÷20=7.2。正方形盒子底部的面积是红+黄+绿+A=20+12+12+7.2=51.2。
巧求面积---割补法
引辅助线法
例1. 下图中四个圆的半径都是5厘米，求阴影部分的面积。
同学们请看图，我们将图形进行割补。 把阴影部分割补成四个半圆形和一个正方形， 求出阴影部分面积就可以了。 2S圆=5×5×3.14×2=157（平方厘米） S正=（5×2）×（5×2）=100（平方厘米） S阴=157+100=257（平方厘米）
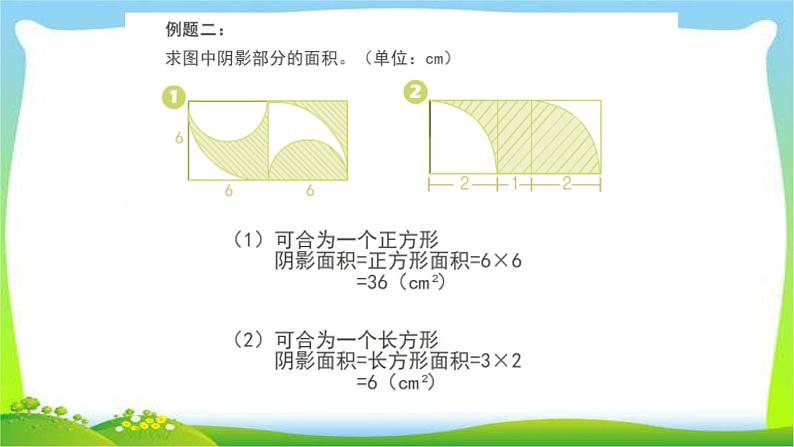
例2.求图中阴影部分的面积
在图中分割的两个正方形中，右边正方形的阴影部分是半径为5的四分之一个圆，在左边正方形中空白部分是半径为5的四分之一个圆。如右图所示，将右边的阴影部分平移到左边正方形中。可以看出，原题图的阴影部分正好等于一个正方形的面积，5×5=25。
例3.求图中阴影部分的面积
　如图所示，将左下角的阴影部分分为两部分，然后按照右下图所示，将这两部分分别拼补在阴影位置。可以看出，原题图的阴影部分等于右下图中AB弧所形成的弓形，其面积等于扇形OAB与三角形OAB的面积之差。　 解： π×4×4÷4-4×4÷2=4.56。
　　例4. 在一个等腰三角形中，两条与底边平行的线段将三角形的两条边等分成三段（见下图），求图中阴影部分的面积占整个图形面积的几分之几。　　
从顶点作底边上的高，得到两个相同的直角三角形。将这两个直角三角形拼成一个长方形见右图。显然，阴影部分正好是长方形的三分之一，所以原题阴影部分占整个图形面积的三分之一。还可以拼成一个平行四边形或将其分成9个三角形。　　　　　
　例5. 如下图所示，在一个等腰直角三角形中，削去一个三角形后，剩下一个上底长5厘米、下底长9厘米的等腰梯形（阴影部分）。求这个梯形的面积。
　　因为不知道梯形的高，所以不能直接求出梯形的面积。可以从等腰直角三角形与正方形之间的联系上考虑。将四个同样的等腰直角三角形拼成一个正方形，图中阴影部分是边长9厘米与边长5厘米的两个正方形面积之差，也是所求梯形面积的4倍。所以所求梯形面积是（9×9-5×5）÷4=14（平方厘米）。
例6.ABC是三个圆的圆心，圆的半径都是10分米，求阴影部分的面积。
我们用割补法，将阴影部分割补成一个半圆形，求出阴影部分面积就可以了。 S半圆=10×10×3.14÷2=157平方分米
例7.如图所示，空白部分占正方形面积的几分之几？ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
将阴影割补成一个长方形，正好占正方形面积的一半。
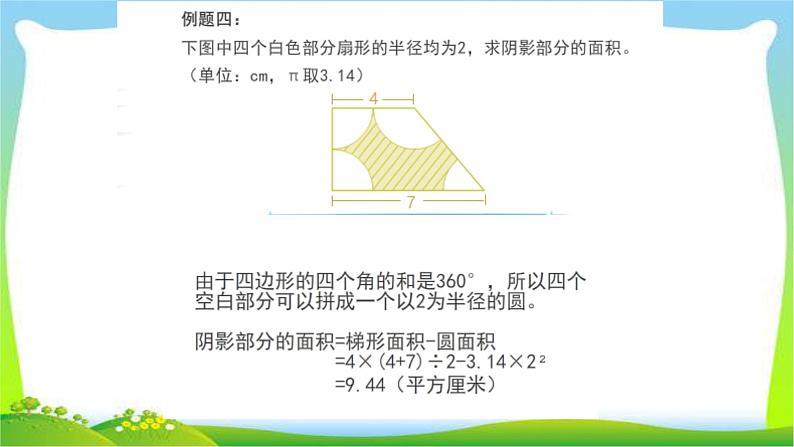
例8.求图中阴影部分的面积（单位：厘米）。
看图，我们用割补法，阴影部分的面积等于扇形的面积减去空白三角形的面积。 S扇=4×4×3.14÷4=12.56（平方厘米）S△=4×4÷2÷2=4（平方厘米）S阴=12.56-4=8.56（平方厘米）
例9.如图，圆O的直径是8厘米，则阴影部分的面积是多少平方厘米？
我们用割补法。看图，阴影部分的面积就是扇形的面积减去正方形的面积。S扇=8×8×3.14÷4=50.24（平方厘米）S正=8×8÷2=32（平方厘米）50.24-32=18.24（平方厘米） 答：阴影部分的面积是18.24平方厘米。
以等腰直角三角形的两条直角边为直径画两个半圆弧（见下图），直角边长4厘米，求图中阴影部分的面积。
巧求面积---引辅助线法
例1.如图所示，平行四边形ABCD的面积是40平方厘米，求图中阴影部分的面积。
连辅助线BD, S△OBD和S△OBC是等底等高的三角形，面积相等，是平行四边形面积的一半。 S阴40÷2÷2=10（平方厘米）
例2.如图，正方形ABCD和正方形EFGC并排放置，BF和EC交于H点，已知AB=4厘米，EF=6厘米，则阴影部分的面积是多少平方厘米？
连接DF,三角形DGH的面积等于三角形DFH的面积，原来阴影部分的面积等于三角形BDF的面积。S大正=6×6=36（平方厘米）S小正=4×4=16 36+16=52 （平方厘米）S△ABD=16÷2=8（平方厘米） S△EFD=（ 6-4）×6÷2=6（平方厘米） S△BFG=（4+6）×6÷2=30（平方厘米） S阴=52-8-6-30=8（平方厘米）
例3. 如图，四边形ABCD是长方形，EC=2DE，F是DG的中点，G是BC中点，阴影部分的面积是20平方厘米，则长方形ABCD的面积是_______。
连接CF , F是中点，S△CFG=S△CFD, S△BDF=S△BFG,G是BC中点，S△CFG=S△BFG=S△CFD=S△BDF,DE:EC=1：2，S△DEF:S△CFE=1：2，S△CFG:S△EFC=3:2, S△CFG=20÷5×3=12（平方厘米） S长=12×4×2=96（平方厘米）
例4.在三角形ABC中，三角形AEO的面积是1，三角形ABO面积是2，三角形BOD的面积是3，则四边形DCEO的面积是多少？
连接OC，把DCEO分成两个三角形ECO和DCO设ECO面积为x，DCO面积为y由条件知，EO：OB＝1：2， AO：OD＝2：3则（AEO+ECO）:DCO＝2 :3ECO：（DCO+BOD）＝1:2即： x：(y+3)=1：2 (x+1)：y=2：3 解得：x=9, y=15所以DCEO＝x+y＝24
例5. 已知E为边长AD的中点,正方形的边长为8厘米，P是CE的中点，求阴影部分的面积。
连结BE,三角形BCE的面积=正方形面积的一半=8×8÷2=32（平方厘米）S△BPC的=S△BCE÷2=16（平方厘米） S△CDE=8×4÷2=16（平方厘米）S△PDC 的面积=S△CDE÷2=8（平方厘米） S阴=S正÷2-16-8=8（平方厘米）
例6.如图△ABC是一个等腰直角三角形，AB=BC=10，求图中阴影部分的面积。（单位：分米）
我们做辅助线。做AE垂直AB,EC平行AB,得到正方形ABCE。S半圆=5×5×3.14÷2=39.25（平方厘米）S正=10×10=100（平方厘米）S△ADE=10×15÷2=75（平方厘米）S阴=（39.25+100-75）÷2=32.125（平方厘米）
例7. 如图，已知长方形ABCD的面积是54平方厘米，BE=2AE，CF=2BF，则四边形ACFE的面积是多少平方厘米？
S△ABC=54÷2=27连接CE。因为AE:EB=1：2，所以：S△ACE:S△BCE=1：2，S△ACE=27÷3=9(平方厘米),S△BCE=27-9=18(平方厘米)因为BF:FC=1：2，所以SBEF:SCEF=1：2，SCEF=18÷3×2=12(平方厘米)SACFE=9+12=21(平方厘米)
如图，正方形ABCD的边长是4厘米，长方形DEFG的顶点G在BC边上，则长方形的面积为多少平方厘米？
等积变形模型说明： 等积变形中的“积”指的是面积，三角形作为最基本图形，任何直线型图形都可分解成若干个三角形，等积变形里主要研究的是三角形面积变换。
等积变形模型实际应用中，常用的3个结论：
结论一的典型应用：夹在一组平行线间的两个三角形若同底，则面积相同。
主要应用场景：正方形、长方形、平形四边行、梯形等
结论一的应用：例：正方形ABCD与正方形GCEF,且正方形ABCD的边长为10cm,求三角形BDF的面积是多少平方厘米？
例：图中正方形GCEF的面积为8,求三角形GAE的面积？
巩固1：三角形ABH的面积为6，求阴影部分面积？
巩固2：已知正方形ABCD的边长为10，正方形BEFG的边长为6，求阴影部分面积？ 
巩固1：三角形ABH的面积为6，求阴影部分面积？答案：6
巩固2：已知正方形ABCD的边长为10，正方形BEFG的边长为6，求阴影部分面积？答案：20 
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。上图中的两个圆半径都是1m，你能求出正方形和圆之间部分的面积吗？
正方形的边长是圆的直径。
可以把正方形看成两个三角形，底是圆的直径，高是圆的半径。
正方形与圆之间的面积：
如果两个圆的半径都是r，结果如下：
（2）“内圆外方”：
议一议 怎样在下面的圆内画一个最大的正方形？
1、请你在下面的正方形里画一个最大的圆，你是怎样确定这个圆的圆心和半径的？半径与正方形的边长有什么关系？
2、下面有直径分别是2cm，3cm，4cm的三个圆，请你分别画出三个正方形，使这三个正方形刚好能够分别盖住这三个圆。
这个正方形的边长是多少厘米？
请填写下表，填写完后，观察表中数据，看看圆与它外切正方形的面积有什么关系？你发现什么？
算一算 请你算出下面的圆内所画的正方形的面积。
请你计算出下面各圆内接正方形的面积并填写书本P72第5题的表格（注：圆的面积用几π表示）
大正方形与小正方形面积比是多少？
每个正方形的边长都是12分米，哪一种切割方法余下的废料（涂色部分）最少？