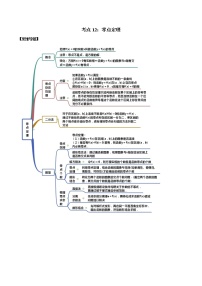
考点12　数系的扩充与复数的引入（解析版）练习题

专题十二　数系的扩充与复数的引入

【基础集训】

考点一　复数的概念及几何意义

1.复数z=(a+1)+(a2-3)i(i为虚数单位),若z<0,则实数a的值是(　　)

A.　　　　　B.1　　　

C.-1　　　　　D.-

【答案】　D

2.设x∈R,i是虚数单位,则“x=2”是“复数z=(x2-4)+(x+2)i为纯虚数”的(　　)

A.充分不必要条件　　　　　

B.充要条件

C.必要不充分条件　　　　　

D.既不充分也不必要条件

【答案】　B

3.已知复数z=,给出下列四个结论:①|z|=2;②z2=2i;③z的共轭复数=-1+i;④z的虚部为i.其中正确结论的个数是(　　)

A.0　　　B.1　　　C.2　　　D.3

【答案】　B

4.已知复数z的共轭复数为,若(1-2i)=5-i(i为虚数单位),则在复平面内,复数z所对应的点位于(　　)

A.第一象限　　　　　B.第二象限            C.第三象限　　　　　D.第四象限

【答案】　A

考点二　复数的运算

5.若(x+2i)i=y-(x,y∈R,i是虚数单位),则x+y=(　　)

A.-1　　　B.1　　　C.3　　　D.-3

【答案】　A

6.已知复数z=(i是虚数单位),则z的实部为(　　)

A.-　　　B.　　　C.-　　　D.

【答案】　B

7.已知i为虚数单位,则=(　　)

A.-1　　　B.1　　　C.-i　　　D.i

【答案】　A

8.若z=2+i,则=(　　)

A.i　　　B.-i　　　C.1　　　D.-1

【答案】　A

【综合集训】

考法一　复数有关概念的解题方法

1.复数(1-i)(3+i)的虚部是(　　)

A.4　　　B.-4　　　C.2　　　D.-2

【答案】　D

2.已知i是虚数单位,复数z=,下列说法正确的是(　　)

A.z的虚部为-i　　　　　B.z对应的点在第一象限

C.z的实部为-1　　　　　D.z的共轭复数为1+i

【答案】　D

3.在复平面内,复数(i为虚数单位)对应的点位于第一象限,则实数m的取值范围是(　　)

A.(-∞,-1)　　　B.(-∞,0)　　　C.(0,+∞)　　　D.(1,+∞)

【答案】　D

4.已知i为虚数单位,复数z=,则以下为真命题的是(　　)

A.z的共轭复数为-

B.z的虚部为

C.|z|=3

D.z在复平面内对应的点在第一象限

【答案】　D

考法二　复数四则运算问题的解法

5.若(1-mi)(m+i)<0,其中i为虚数单位,则m的值为(　　)

A.-1　　　B.-2　　　C.-3　　　D.-4

【答案】　A

6.复数(-1+3i)(3-i)=(　　)

A.10　　　B.-10　　　C.10i　　　D.-10i

【答案】　C

7.双基测试,1)=(　　)

A.i　　　B.-i　　　C.2i　　　D.-2i

【答案】　A

8.若复数z满足(2+i)z=4-(1+i)2(其中i是虚数单位),则|z|=(　　)

A.2　　　B.4　　　C.　　　D.2

【答案】　A

题组一

考点一　复数的概念及几何意义

1.复数(i为虚数单位)的共轭复数是(　　)

A.1+i　　　B.1-i　　　C.-1+i　　　D.-1-i

【答案】　B

2.设z=-3+2i,则在复平面内对应的点位于(　　)

A.第一象限　　　B.第二象限　　　C.第三象限　　　D.第四象限

【答案】　C

3.已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是(　　)

A.(-3,1)　　　　　B.(-1,3)

C.(1,+∞)　　　　　D.(-∞,-3)

【答案】　A

4.在复平面内,复数的共轭复数对应的点位于(　　)

A.第一象限　　　　　B.第二象限

C.第三象限　　　　　D.第四象限

【答案】　D

5.若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是(　　)

A.(-∞,1)　　　B.(-∞,-1)　　　C.(1,+∞)　　　D.(-1,+∞)

【答案】　B

6.已知a∈R,i是虚数单位.若z=a+i,z·=4,则a=(　　)

A.1或-1　　　B.或-　　　C.-　　　D.

【答案】　A

7.若复数z满足2z+=3-2i,其中i为虚数单位,则z=(　　)

A.1+2i　　　B.1-2i　　　C.-1+2i　　　D.-1-2i

【答案】　B

8.设有下面四个命题:

p1:若复数z满足∈R,则z∈R;

p2:若复数z满足z2∈R,则z∈R;

p3:若复数z1,z2满足z1z2∈R,则z1=;

p4:若复数z∈R,则∈R.

其中的真命题为(　　)

A.p1,p3　　　　　B.p1,p4

C.p2,p3　　　　　D.p2,p4

【答案】　B

9.若复数z满足i·z=1+2i,其中i是虚数单位,则z的实部为　　　　. 

【答案】　2

考点二　复数的运算

10.若z(1+i)=2i,则z=(　　)

A.-1-i　　　B.-1+i　　　C.1-i　　　D.1+i

【答案】　D

11.设z=+2i,则|z|=(　　)

A.0　　　B.　　　C.1　　　D.

【答案】　C

12.=(　　)

A.--i　　　　　B.-+i

C.--i　　　　　D.-+i

【答案】　D

13.(1+i)(2-i)=(　　)

A.-3-i　　　B.-3+i　　　C.3-i　　　D.3+i

【答案】　D

14.=(　　)

A.1+2i　　　B.1-2i　　　C.2+i　　　D.2-i

【答案】　D

15.设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=(　　)

A.1　　　B.　　　C.　　　D.2

【答案】　B

16.设复数z满足=i,则|z|=(　　)

A.1　　　B.　　　C.　　　D.2

【答案】　A

17.若复数z满足=i,其中i为虚数单位,则z=(　　)

A.1-i　　　B.1+i　　　C.-1-i　　　D.-1+i

【答案】　A

18.i是虚数单位,则的值为　　　　. 

【答案】　

19.复数z=(i为虚数单位),则|z|=　　　　. 

【答案】　

20.i是虚数单位,复数=　　　　. 

【答案】　4-i

21.已知a,b∈R,(a+bi)2=3+4i(i是虚数单位),则a2+b2=　　　　,ab=　　　　. 

【答案】　5;2

题组二

考点一　复数的概念及几何意义

1.i为虚数单位,i607的为(　　)

A.i　　　B.-i　　　C.1　　　D.-1

【答案】　A

2.若复数z=i(3-2i)(i是虚数单位),则=(　　)

A.2-3i　　　B.2+3i　　　C.3+2i　　　D.3-2i

【答案】　A

3.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=(　　)

A.-5　　　B.5　　　C.-4+i　　　D.-4-i

【答案】　A

4.已知复数(a+2i)(1+i)的实部为0,其中i为虚数单位,则实数a的值是　　　　. 

【答案】　2

5.复数z=(1+2i)(3-i),其中i为虚数单位,则z的实部是　　　　. 

【答案】　5

6.i是虚数单位,若复数(1-2i)(a+i)是纯虚数,则实数a的值为　　　　. 

【答案】　-2

考点二　复数的运算

7.若a为实数,且(2+ai)(a-2i)=-4i,则a=(　　)

A.-1　　　B.0　　　C.1　　　D.2

【答案】　B

8.复数i(2-i)=(　　)

A.1+2i　　　B.1-2i　　　C.-1+2i　　　D.-1-2i

【答案】　A

9.已知=1+i(i为虚数单位),则复数z=(　　)

A.1+i　　　B.1-i　　　C.-1+i　　　D.-1-i

【答案】　D

10.=(　　)

A.1+i　　　B.1-i　　　C.-1+i　　　D.-1-i

【答案】　D

11.设复数z满足(1-i)z=2i,则z=(　　)

A.-1+i　　　B.-1-i　　　C.1+i　　　D.1-i

【答案】　A

12.若复数z满足(3-4i)z=|4+3i|,则z的虚部为(　　)

A.-4　　　B.-　　　C.4　　　D.

【答案】　D

13.已知复数z=(1+i)(1+2i),其中i是虚数单位,则z的模是　　　　. 

【答案】　

14.设a∈R.若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a=　　　　. 

【答案】　-1

15.已知a,b∈R,i是虚数单位.若(1+i)(1-bi)=a,则的值为　　　　. 

【答案】　2

16.设复数a+bi(a,b∈R)的模为,则(a+bi)(a-bi)=　　　　. 

【答案】　3

17.设复数z满足z2=3+4i(i是虚数单位),则z的模为　　　　. 

【答案】　

模拟预测

一、单项选择题(每题5分,共55分)

1.已知a+bi(a,b∈R)是的共轭复数,则a+b=(　　)

A.-1　　　B.-　　　C.　　　D.1

【答案】　D

2.已知复数z=,则下列说法正确的是(　　)

A.复数z的实部为3

B.复数z的虚部为i

C.复数z的共轭复数为+i

D.复数z的模为1

【答案】　C

3.已知i为虚数单位,则复数(2-i)i3的虚部为(　　)

A.-2　　　B.2　　　C.-1　　　D.1

【答案】　A

4.已知复数z=(i为虚数单位),则复数z的模等于(　　)

A.　　　B.　　　C.　　　D.

【答案】　A

5.已知i是虚数单位,则复数z=的共轭复数的虚部为(　　)

A.-4i　　　B.-4　　　C.4i　　　D.4

【答案】　D

6.已知复数z满足z+2i=3+zi(i为虚数单位),则在复平面内z对应的点位于(　　)

A.第一象限　　　　　B.第二象限

C.第三象限　　　　　D.第四象限

【答案】　A

7.设i为虚数单位,1-i=,则实数a=(　　)

A.2　　　B.1　　　C.0　　　D.-1

【答案】　C

8.已知i是虚数单位,复数z=+i2 018在复平面内所对应的点位于(　　)

A.第一象限　　　B.第二象限　　　C.第三象限　　　D.第四象限

【答案】　B

9.已知复数z=是纯虚数,其中a是实数,则z等于(　　)

A.2i　　　B.-2i　　　C.i　　　D.-i

【答案】　A

10.若复数z=为纯虚数,则实数a的值为(　　)

A.1　　　B.0　　　C.-　　　D.-1

【答案】　D

11.复数=A+Bi(m、A、B∈R),且A+B=0,则m的值是(　　)

A.-　　　B.　　　C.　　　D.2

【答案】　A

二、多项选择题(共5分)

12.欧拉公式eix=cos x+isin x(其中i为虚数单位,x∈R)是由瑞士著名数学家欧拉创立的,该公式将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关联,在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”.依据欧拉公式,下列选项正确的是(　　)

A.=-i　　　　        　B.为纯虚数

C.复数eπi的模等于1　　　　　D.复数的共轭复数为-i

【答案】　BCD

三、填空题(每题5分,共10分)

13.在复平面内,复数z=对应的点位于第三象限,则实数a的取值范围是　　　. 

【答案】　(-∞,0)

14.已知i为虚数单位,若复数z=(a∈R)的虚部为-3,则|z|=　　　　. 

【答案】