期末练习试卷 2021-2022学年沪教版（上海）八年级上册数学（word版 含答案）

这是一份期末练习试卷 2021-2022学年沪教版（上海）八年级上册数学（word版 含答案），共17页。试卷主要包含了下列命题是真命题的个数为，下列说法正确的是，计算×的结果是　 　等内容，欢迎下载使用。

2021-2022学年沪教新版八年级上学期数学期末练习试卷
一．选择题（共6小题，满分12分，每小题2分）
1．下列函数中，y与x成正比例函数关系的是（　　）
A．y＝x﹣1 B．y＝﹣x C．y＝5（x+1） D．y＝
2．下列一元二次方程中，有两个相等的实数根的是（　　）
A．x2﹣2x＝0 B．x2+4x＝﹣4 C．2x2﹣4x+3＝0 D．3x2＝5x﹣2
3．下列二次根式中，与是同类二次根式的是（　　）
A． B． C． D．
4．若一次函数y＝kx+b的图象经过第一、二、四象限，则（　　）
A．k＞0，b＞0 B．k＞0，b＜0 C．k＜0，b＜0 D．k＜0，b＞0
5．下列命题是真命题的个数为（　　）
①两条直线被第三条直线所截，内错角相等．
②三角形的内角和是180°．
③在同一平面内，平行于同一条直线的两条直线平行．
④相等的角是对顶角．
⑤两点之间，线段最短．
A．2 B．3 C．4 D．5
6．下列说法正确的是（　　）
A．在△ABC中，若∠A：∠B：∠C＝3：4：5，则△ABC是直角三角形
B．在直角△ABC中，一边长为3，另一边长为4，则第三边长一定为5
C．在△ABC中，若∠A＝∠B﹣∠C，则△ABC是直角三角形
D．三边长分别为1，，的三角形不是直角三角形
二．填空题（共12小题，满分36分，每小题3分）
7．式子在实数范围内有意义，则x的取值范围是 　 　．
8．计算×的结果是　 　．
9．一元二次方程x2＝x的解为　 　．
10．当a＝　 　时，函数y＝（a﹣1）x|a|是关于x的正比例函数．
11．已知反比例函数y＝图象经过第四象限的点（1，a）和（2，b），则a与b的大小关系是　 　．
12．在小华的某个微信群中，若每人给其他成员都发一个红包，该微信群共发了90个红包，那么这个微信群共有　 　人．
13．如图，四边形ABHK是边长为6的正方形，点C、D在边AB上，且AC＝DB＝1，点P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP，E、F分别为MN、QR的中点，连接EF，设EF的中点为G，则当点P从点C运动到点D时，点G移动的路径长为　 　．

14．如图，在小正方形的边长为1的网格中，点A，B，C在格点上，D是AB与网格线的交点，则CD的长是　 　．

15．定义：对于平面直角坐标系xOy中的线段PQ和点M，在△MPQ中，当PQ边上的高为2时，称M为PQ的“等高点”，称此时MP+MQ为PQ的“等高距离”．
（1）若点P的坐标为（1，2），点Q的坐标为（4，2），则在点A（1，0），B（，4），C（0，3）中，PQ的“等高点”是点　 　；
（2）若P（0，0），PQ＝2，当PQ的“等高点”在y轴正半轴上且“等高距离”最小时，点Q的坐标是　 　．
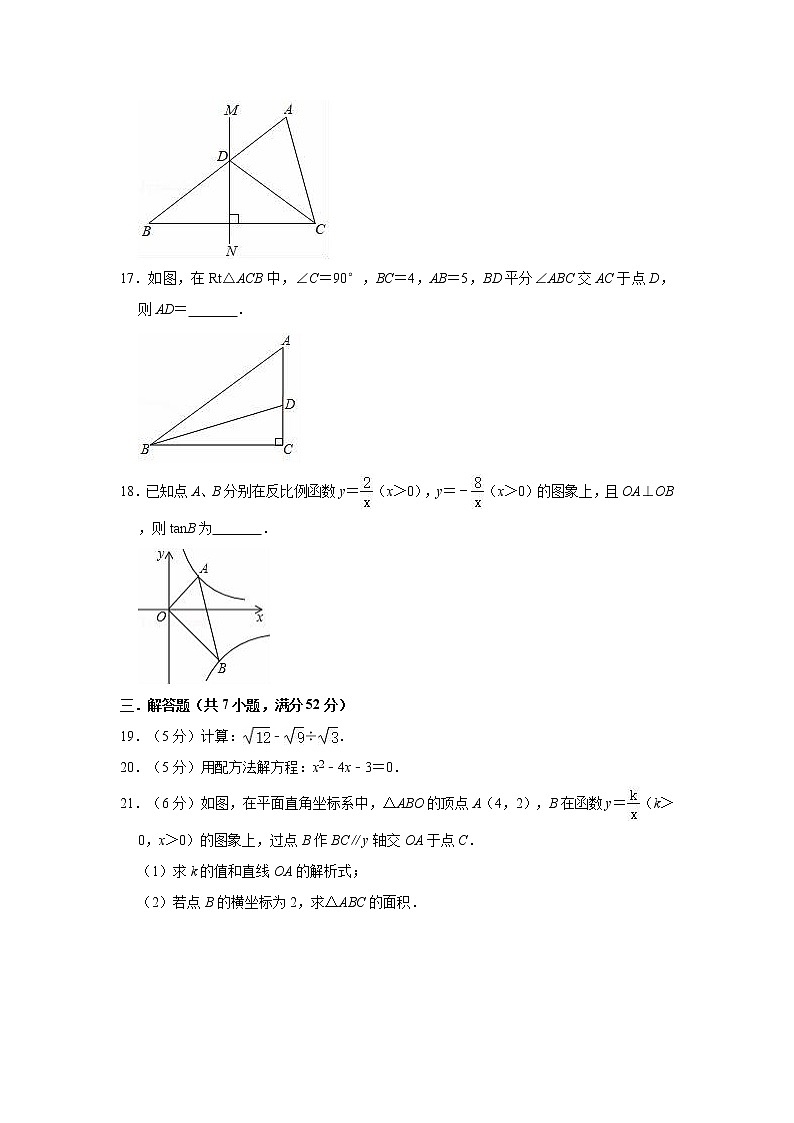
16．如图，在△ABC中，BC的垂直平分线MN交AB于点D，若BD＝3，AD＝2，则AC的长度x取值范围为　 　．

17．如图，在Rt△ACB中，∠C＝90°，BC＝4，AB＝5，BD平分∠ABC交AC于点D，则AD＝　 　．

18．已知点A、B分别在反比例函数y＝（x＞0），y＝﹣（x＞0）的图象上，且OA⊥OB，则tanB为　 　．

三．解答题（共7小题，满分52分）
19．（5分）计算：﹣÷．
20．（5分）用配方法解方程：x2﹣4x﹣3＝0．
21．（6分）如图，在平面直角坐标系中，△ABO的顶点A（4，2），B在函数y＝（k＞0，x＞0）的图象上，过点B作BC∥y轴交OA于点C．
（1）求k的值和直线OA的解析式；
（2）若点B的横坐标为2，求△ABC的面积．

22．（6分）已知：如图，△ABC中，∠ACB＝90°，∠A＝30°，CD⊥AB于D，点E在AB的延长线上，∠E＝45°，若AB＝8，求BE的长．

23．（8分）如图，四边形ABCD中，∠BAD＝90°，∠DCB＝90°，E、F分别是BD、AC的中点．
（1）请你猜测EF与AC的位置关系，并给予证明；
（2）当AC＝24，BD＝26时，求EF的长．

24．（10分）如图，将矩形OABC放置在平面直角坐标系中，使点A和点C分别落在x轴和y轴的正半轴上，OA＝2，OC＝3，E是AB中点，反比例函数图象过点E且和BC相交于点F．
（1）求反比例函数与直线EF的解析式；
（2）连接OE，OF，求四边形OEBF的面积．

25．（12分）如图，在Rt△ABC中，∠ACB＝90°，BC＝AC＝2，D为AB中点，E，F分别是AC，BC上的动点，且满足∠EDF＝90°．
（1）求证：DE＝DF；
（2）求四边形CFDE的面积；
（3）求△CEF周长的最小值（结果保留根号）．


参考答案与试题解析
一．选择题（共6小题，满分12分，每小题2分）
1．解：A．y＝x﹣1，y是x的一次函数，因此选项A不符合题意；
B．y＝﹣x，y是x的正比例函数，因此选项B符合题意；
C．y＝5（x+1）＝5x+5，y是x的一次函数，因此选项C不符合题意；
D．y＝，y是x的反比例函数，因此选项D不符合题意；
故选：B．
2．解：A．Δ＝（﹣2）2﹣4×1×0＝4＞0，则方程有两个不相等的实数根，所以A选项不符合题意；
B．x2+4x+4＝0，Δ＝42﹣4×1×4＝0，则方程有两个相等的实数根，所以B选项符合题意；
C．Δ＝（﹣4）2﹣4×2×3＝﹣8＜0，则方程没有实数根，所以C选项不符合题意；
D．3x2﹣5x+2＝0，Δ＝（﹣5）2﹣4×3×2＝1＞0，则方程有两个不相等的实数根，所以D选项不符合题意．
故选：B．
3．解：A、与被开方数不同，不是同类二次根式；
B、＝2与被开方数不同，不是同类二次根式；
C、＝2与被开方数不同，不是同类二次根式；
D、＝2与被开方数相同，是同类二次根式．
故选：D．
4．解：∵一次函数y＝kx+b的图象经过第一、二、四象限，
∴k＜0，b＞0，
故选：D．
5．解：①两条平行线被第三条直线所截，内错角相等，原命题是假命题．
②三角形的内角和是180°，是真命题．
③在同一平面内，平行于同一条直线的两条直线平行，是真命题．
④相等的角不一定是对顶角，原命题是假命题．
⑤两点之间，线段最短，是真命题；
故选：B．
6．解：A、在△ABC中，若∠A：∠B：∠C＝3：4：5，则∠A＝×180°＝45°，∠B＝×180°＝60°，∠C＝×180°＝75°，则△ABC不是直角三角形，所以A选项的说法错误；
B、在Rt△ABC中，若两边长分别为3和4，则第三边长为5或，所以B选项的说法错误；
C、在△ABC中，若∠A＝∠B﹣∠C，
∴∠A+∠C＝∠B＝180°＝90°，那么这个三角形是直角三角形，所以C选项的说法正确；
D、三边长分别为1，，，则12+（）2＝（）2，∴三边长分别为1，，的三角形是直角三角形，所以D选项的说法错误．
故选：C．
二．填空题（共12小题，满分36分，每小题3分）
7．解：由题意得：5﹣x≥0，
解得：x≤5，
故答案为：x≤5．
8．解：原式＝＝＝2．
故答案为：2．
9．解：x2＝x，
移项得：x2﹣x＝0，
∴x（x﹣1）＝0，
x＝0或x﹣1＝0，
∴x1＝0，x2＝1．
故答案为：x1＝0，x2＝1．
10．解：∵y＝（a﹣1）x|a|是关于x的正比例函数，
∴|a|＝1且a﹣1≠0，
解得：a＝﹣1，
当a＝﹣1时，函数y＝（a﹣1）x|a|是关于x的正比例函数．
故答案为：﹣1．
11．解：∵反比例函数y＝图象经过第四象限的点（1，a）和（2，b），
在四象限，y随x的增大而增大，
∴a＜b．
故答案为a＜b．
12．解：设这个微信群共有x人，则每人需发（x﹣1）个红包，
依题意得：x（x﹣1）＝90，
整理得：x2﹣x﹣90＝0，
解得：x1＝10，x2＝﹣9（不合题意，舍去）．
故答案为：10．
13．解：如图，

设KH的中点为S，连接PE，PF，SE，SF，PS，
∵E为MN的中点，S为KH的中点，
∴ME＝MN，KS＝KH，
∵，∠AME＝∠AKS＝90°，
∴△AEM∽△ASK，
∴∠AEM＝∠ASK，
∴A，E，S共线，
同理可得：B、F、S共线，
由△AME∽△PQF，得∠SAP＝∠FPB，
∴ES∥PF，
△PNE∽△BRF，得∠EPA＝∠FBP，
∴PE∥FS，
则四边形PESF为平行四边形，则G为PS的中点，
∴G的轨迹为△CSD的中位线，
∵CD＝AB﹣AC﹣BD＝6﹣1﹣1＝4，
∴点G移动的路径长．
故答案为：2．
14．解：∵AC＝＝，BC＝＝2，AB＝＝5，
∴AC2+BC2＝25＝AB2，
∴∠ACB＝90°，
∴CD＝AB＝，
故答案为：．
15．解：（1）①∵P（1，2），Q（4，2），
∴在点A（1，0），B（，4）到PQ的距离为2．
∴PQ的“等高点”是A或B，
故答案为：A或B；
（2）如图2，过PQ的“等高点”M作MN⊥PQ于点N，

∴PQ＝2，MN＝2．
设PN＝x，则NQ＝2﹣x，
在Rt△MNP和Rt△MNQ中，由勾股定理得：
MP2＝22+x2＝4+x2，MQ2＝22+（2﹣x）2＝x2﹣4x+8，
∴MP2+MQ2＝2x2﹣4x+12＝2（x﹣1）2+10，
∵MP2+MQ2≤（MP+MQ）2，
∴当MP2+MQ2最小时MP+MQ也最小，此时x＝1，
即PN＝NQ，
∴△MPQ为等腰三角形，
∴MP＝MQ＝＝，
如图3，设Q坐标为（x，y），过点Q作QE⊥y轴于点E，

则在Rt△MNP和Rt△MNQ中由勾股定理得：
QE2＝QP2﹣OE2＝22﹣y2＝4﹣y2，QE2＝QM2﹣ME2＝（）2﹣（﹣y）2＝2y﹣y2，
∴4﹣y2＝2y﹣y2，
解得y＝，
QE2＝4﹣y2＝4﹣（）2＝，
当点Q在第一象限时x＝，当点Q在第二象限时x＝﹣，
∴Q（，）或Q（﹣，），
故答案为：Q（，）或Q（﹣，）．
16．解：∵MN是线段BC的垂直平分线，
∴DC＝BD＝3，
在△ADC中，3﹣2＜AC＜3+2，即1＜x＜5，
故答案为：1＜x＜5．
17．解：在Rt△ACB中，∠C＝90°，BC＝4，AB＝5，
∴AC＝＝3，
过D作DE⊥AB于E，
∵BD平分∠ABC，∠C＝90°，
∴CD＝DE，
在Rt△BCD与Rt△BED中，
∴Rt△BCD≌Rt△BED（HL），
∴BE＝BC＝4，
∴AE＝1，
∵AD2＝DE2+AE2，
∴AD2＝（3﹣AD）2+12，
∴AD＝，
故答案为：．

18．解：过A作AC⊥y轴，过B作BD⊥y轴，可得∠ACO＝∠BDO＝90°，
∴∠AOC+∠OAC＝90°，
∵OA⊥OB，
∴∠AOC+∠BOD＝90°，
∴∠OAC＝∠BOD，
∴△AOC∽△OBD，
∵点A、B分别在反比例函数y＝（x＞0），y＝﹣（x＞0）的图象上，
∴S△AOC＝1，S△OBD＝4，
∴S△AOC：S△OBD＝1：4，即OA：OB＝1：2，
则在Rt△AOB中，tan∠ABO＝．
故答案为：

三．解答题（共7小题，满分52分）
19．解：﹣÷
＝2﹣
＝．
20．解：移项得x2﹣4x＝3，
配方得x2﹣4x+4＝3+4，即（x﹣2）2＝7，
开方得x﹣2＝±，
所以x1＝2+，x2＝2﹣．
21．解：（1）∵点A（4，2）在函数y＝（k＞0，x＞0）的图象上，
∴k＝4×2＝8，
故A坐标为（3，2），
设直线OA的解析式为y＝mx，代入点A（4，2），
得2＝4m，m＝，
即直线OA的解析式为y＝x；

（2）如图，作AD⊥BC于点D，
∵B在函数y＝的图象上，点B的横坐标为2，
∴当x＝2时，y＝＝4，
∴B（2，4）．
∵直线OA的解析式为y＝x，
∴当x＝2时，y＝×2＝1，
∴C（2，1），
∴BC＝4﹣1＝3，
又AD＝4﹣2＝2，
∴S△ABC＝BC•AD＝×3×2＝3．

22．解：∵∠ACB＝90°，∠A＝30°，AB＝8，
∴BC＝AB＝×8＝4，
∵CD⊥AB，
∴∠BCD+∠ABC＝90°，
又∵∠A+∠ABC＝90°，
∴∠BCD＝∠A＝30°，
∴BD＝BC＝×4＝2，
在Rt△BCD中，CD＝＝＝2，
∵∠E＝45°，
∴∠DCE＝90°﹣45°＝45°，
∴∠DCE＝∠E，
∴DE＝CD＝2，
∴BE＝DE﹣BD＝2﹣2．
23．解：（1）EF⊥AC，证明过程如下：
连接AE、CE，

∵∠BAD＝90°，E为BD中点，
∴AE＝DB，
∵∠DCB＝90°，
∴CE＝BD，
∴AE＝CE，
∵F是AC中点，
∴EF⊥AC；
（2）∵AC＝24，BD＝26，E、F分别是边AC、BD的中点，
∴AE＝CE＝13，CF＝12，
∵EF⊥AC．
∴EF＝＝5．
24．解：（1）∵OA＝2，OC＝3，E是AB中点，
∴B（2，3），E（2，），
设反比例函数的解析式为y＝，
把E（2，）代入得，
解得：k1＝3，
∴反比例函数的解析式为y＝，
∴点F在BC上，
∴yF＝3，
把yF＝3代入y＝得，xF＝1，
∴F（1，3），
设直线EF的解析式为y＝k2x+b，
把E（2，），F（1，3）代入得，，
解得：，
∴直线EF的解析式为y＝﹣x+；
（2）S四边形OEBF＝S矩形OABC﹣S△OCF﹣S△OAE＝2×3﹣×1×3﹣×2×＝3．
25．（1）证明：连接CD．
∵∠ACB＝90°，BC＝AC，AD＝BD，
∴CD⊥AB，CD＝DA＝DB，∠A＝∠B＝∠BCD＝45°，
∵∠EDF＝∠CDB＝90°，
∴∠CDE＝∠BDF，
在△CDE和△BDF中，
，
∴△DEC≌△DFB（ASA），
∴ED＝FD．

（2）解：∵△DEC≌△DFB，
∴S△EDC＝S△FDB，
∴S四边形CFDE＝S△CDB＝S△ABC＝××2×2＝1．

（3）∵△DEC≌△DFB，
∴CE＝BF，
∴EC+CF＝CF+BF＝BC＝2，
∴当EF的长最小时，△ECF的周长最小，
∵△DEF是等腰三角形，
∴当DF最小时，EF的长最小，
∵DF⊥BC时，DF的值最小，此时DF＝AC＝1，
∴EF＝，
∴△DEF的周长的最小值为2+．