

甘肃省酒泉市金塔县2021-2022学年九年级上学期期末考试数学试题(word版 含答案)
展开
这是一份甘肃省酒泉市金塔县2021-2022学年九年级上学期期末考试数学试题(word版 含答案),共7页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。
2021~2022学年第一学期期末试卷九年级数学 一、选择题(每小题3分,共30分)1.下列方程中是关于x的一元二次方程的是( )A.x2+=0 B.ax2+bx+c=0 C.(x-1)(x+2)=1 D.3x-2xy-5y2=02.如右图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )A. B. C. D. 3.已知是的黄金分割点(),若,则BC的长为( )A.() B.() C.() D.()4.用配方法解一元二次方程,配方后的结果是( )A. B. C. D.5.矩形具有而菱形不具有的性质是( )A.对角线相等 B.对角线平分一组对角C.对角线互相平分 D.对角线互相垂直6.若点都在反比例函数的图象上,则的大小关系是( )A. B. C. D.7.李明参加的志愿服务团队共有A、B、C、D四个服务项目,其中每个服务项目又分为第一小组和第二小组,则李明分到A项目的第一小组的概率是( )A. B. C. D.8.如右图,一块矩形ABCD绸布的长AB=a,宽AD=1,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )A. B. C. D.9.如右图,四边形ABCD是菱形,AC=8,tan∠DAC=,DH⊥AB于H,则点D到AB边距离等于( )A.4 B.5 C. D.10.某小区A楼居民今年从三月开始到五月底全部接种新冠疫苗.已知该楼常驻人口285人,三月已有60人接种新冠疫苗,四月、五月实现接种人数较前一个月的平均增长率为x,则下面所列方程正确的是( )A.60(1+x)2=285 B.60(1﹣x)2=285C.60(1+x)+60(1+x)2=285 D.60+60(1+x)+60(1+x)2=285二、填空题(每小题3分,共30分)11.方程x(x﹣3)=x﹣3的根是 .12.若反比例函数的图象经过点A(-2,4)和点B(8,a),则a的值为______.13.在中,DE∥BC,分别交、于点、,已知,,,则______.14.计算:×﹣sin45°=_______.15.在中,,,则________.16.在,3,5,7中随机选取一个数记为,再从余下的数中随机取一个数记为,则一次函数经过一、三、四象限的概率为______.17.如图,在长为20m,宽为12m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为整个矩形面积的,如果设道路的宽为x m,则根据题意可列出方程_________.18.在和中,,,,,则 时,和相似.19.若一个三角形的三边长均满足方程x2﹣6x+8=0,则此三角形的周长为____.20.如图,下列各图中的三个数之间具有相同规律.依此规律用含m,n的代数式表示y,则y= .三、计算题(每小题5分,共10分)21. 6tan230°﹣ sin60°﹣2tan45° 22.解方程: 四、作图题(共6分)23.如图所示,图中的小方格都是边长为1的正方形,△ABC与 是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;(2)直接写出△ABC与 的位似比; (3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系并直接写出 各顶点的坐标。五、解答题(共44分)24.(本题6分)在一次试验中,每个电子元件的状态有两种可能:在一定时间段内电流可正常通过的状态即“通电”状态;在一定时间段内电流无法通过的状态即“断开”状态,并且这两种状态的可能性相等.如图,请完成下面问题:(1)计算在一定时间段内,A、B之间电流能够正常通过的概率;(2)用树状图或表格计算在一定时间段内C、D之间电流能够正常通过的概率. 25.(本题6分)如图,从楼层底部处测得旗杆的顶端处的仰角是,从楼层顶部处测得旗杆的顶端处的仰角是,已知楼层的楼高为米.求旗杆的高度约为多少米?(参考数据:)
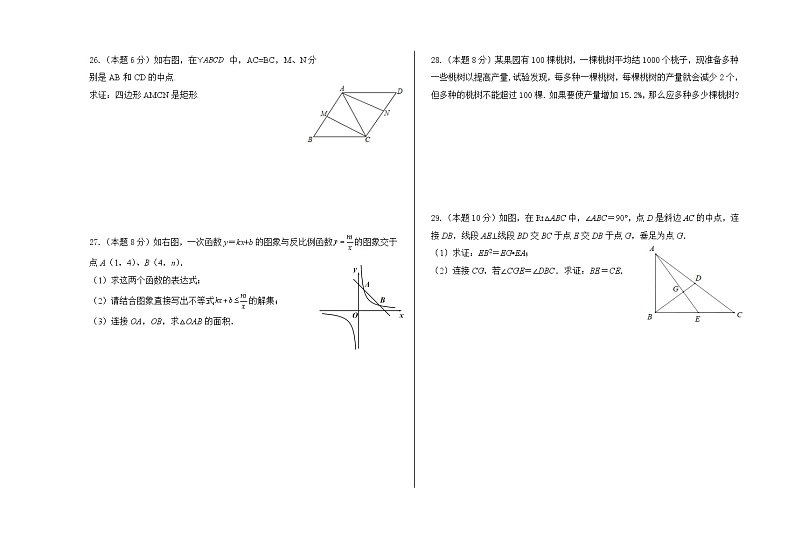
26.(本题6分)如右图,在 中,AC=BC,M、N分别是AB和CD的中点.求证:四边形AMCN是矩形. 27.(本题8分)如右图,一次函数y=kx+b的图象与反比例函数的图象交于点A(1,4)、B(4,n).(1)求这两个函数的表达式;(2)请结合图象直接写出不等式的解集;(3)连接OA,OB,求△OAB的面积. 28.(本题8分)某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵桃树的产量就会减少2个,但多种的桃树不能超过100棵.如果要使产量增加15.2%,那么应多种多少棵桃树? 29.(本题10分)如图,在Rt△ABC中,∠ABC=90°,点D是斜边AC的中点,连接DB,线段AE⊥线段BD交BC于点E交DB于点G,垂足为点G.(1)求证:EB2=EG•EA;(2)连接CG,若∠CGE=∠DBC.求证:BE=CE. 2021~2022学年第一学期期末试卷九年级数学答案一、选择题(每小题3分,共30分)C 2.C 3.A 4.A 5.A 6.B 7.A 8.B 9.C 10.D 二、填空题(每小题3分,共30分) 1. x1=3,x2=1 2. -1 3. 1.5 4. 5. 6. (20﹣x)(12﹣x)= ×20×12 8. 2cm或4.5cm 9. 6或12或10 10. m(n+2)三、解答题21.原式=6×()2﹣×﹣2×1 --------------2分=6×﹣﹣2 ---------------------------------------3分=2﹣﹣2 ---------------------------------------4分=﹣ ---------------------------------------5分22.解:展开,得3x2 +9x+2x+6=x+14 --------------------------------------------1分整理,得3x2 +10x-8=0 ----------------------------------------------------2分△=102 -4×3×(-8)=196------------------------------------------------------3分 ----------------------------------------------4分 ----------------------------------5分四、作图题(1)如图,各对应点连线所在直线的交点即为位似中心O;------------------2分 (2)△ABC与 的位似比为 -----------------------------------4分(3)---------------------6分五、解答题24.(1)画树状图如下: ------------------------------------------------2分共有4种等可能的结果,A、B之间电流能够正常通过的结果有1种,∴A、B之间电流能够正常通过的概率为 -----------------------------------3分(2)画树状图如下: ---------------------------------------------5分共有4种等可能的结果,在一定时间段内C、D之间电流能够正常通过的结果有3种,∴在一定时间段内C、D之间电流能够正常通过的概率为 --------------------------6分25.解:如右图,作于点,-------------------------------------1分由题意可知:,设,则,------------------------------------2分 ,--------------------------------------5分即: -------------------------------------------4分从而x=9,则DC=3+9=12,-------------------------------5分答:旗杆的高度约为米.-----------------------------6分26.(1)∵四边形ABCD是平行四边形∴AB=CD, AB∥CD∴AM∥CN -------------------------------------------1分 ∵M、N分别是AB和CD的中点 ∴AM= AB,CN= CD ∴AM=CN --------------------------------------------------------------------2分∵AM∥CN∴四边形AMCN是平行四边形 -------------------------------------------3分∵AC=BC∴△ACB是等腰三角形-------------------------------------------------------4分∵M是AB的中点∴CM是△ACB的边AB上的中线∴CM是△ACB的边AB上的高--------------------------------------------5分∴∠AMC=90°∴四边形AMCN是矩形----------------------- ------------------------------6分27.解:(1)把点A(1,4)代入,得: ,∴反比例函数的解析式为,-------------------------1分∵B(4,n)在反比例函数图象上,∴ ,从而点 ,------------------------2分把点A(1,4),点代入 ,得: ,解得: ,∴一次函数的解析式为 ;--------------------3分(2)观察图象,得:当 或 时,,∴不等式的解集为 或;-------------------------5分(3)如图,连结OA,OB,设直线与x轴交于点D,与y轴交于点C,当 时, ,当 时, ,∴点 ,-------------------------6分∴OC=5,OD=5,∵点A(1,4),点,∴ -----------------8分28.解:设多种x棵树,则根据题意得:------------------ ------------------------------------------1分(100+x ) ( 1000—2x )=100×1000× ( 1+15.2%) ( 0<x<100 ) -----------------------------4分整理,得:x2—400x+7600=0 ---------- -------------------------------------------------------5分所以 ( x—20 ) ( x—380 )=0 解得x1=20, x2=380(舍去) -------- ------------------------------------------------------7分答:应多种20棵桃树. --------- ------------------------------------------------------8分29.解:(1)证明:∵∴∵∴---------------------------1分∵∴------------------------- --2分∴---------------------------------3分∴----------------------------4分(2)在中,点D是斜边的中点∴∴--------------------------5分∵∴-------------------------6分∵∴--------------------------7分∴∴--------------------------8分由(1)得∴------------------------------9分∴--------------------------------10分
相关试卷
这是一份甘肃省酒泉市金塔县2024届九年级上学期期末考试数学试卷(含解析),共10页。试卷主要包含了下列命题是真命题的是,关于的图象,下列叙述正确的是,点A,二次函数y=ax2+bx+c个,已知,则的值是 等内容,欢迎下载使用。
这是一份甘肃省酒泉市金塔县2024届九年级上学期期末考试数学试卷(含解析),共10页。试卷主要包含了下列命题是真命题的是,关于的图象,下列叙述正确的是,点A,二次函数y=ax2+bx+c个,已知,则的值是 等内容,欢迎下载使用。
这是一份甘肃省酒泉市金塔县2023-2024学年八年级上学期期末考试数学试卷(含答案),共7页。试卷主要包含了请将答案正确填写在答题卡上,已知点A,下列选项不是方程的解的是,若有意义,则实数x的取值范围为等内容,欢迎下载使用。









