高中人教版（中职）8.4 直线与圆的位置关系课文课件ppt

这是一份高中人教版（中职）8.4 直线与圆的位置关系课文课件ppt，共14页。PPT课件主要包含了半径为，引入问题，用图形表示如下，直线和圆相交，直线和圆相切，直线和圆相离等内容，欢迎下载使用。
直线方程的一般式为:____________________________
2.圆的标准方程为：______________
3.圆的一般方程：__________________________________
圆心为________
Ax+By+C=0(A,B不同时为零)
(x-a)2+(y-b)2=r2
x2+y2+Dx+Ey+F=0(其中D2+E2-4F>0)圆心为 半径为
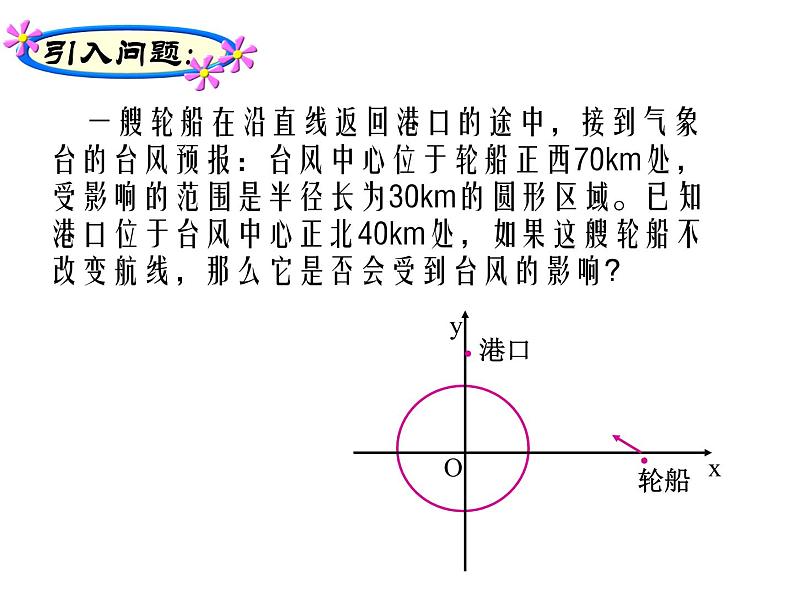
一艘轮船在沿直线返回港口的途中，接到气象台的台风预报：台风中心位于轮船正西70km处，受影响的范围是半径长为30km的圆形区域。已知港口位于台风中心正北40km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？
你知道直线和圆的位置关系有几种？
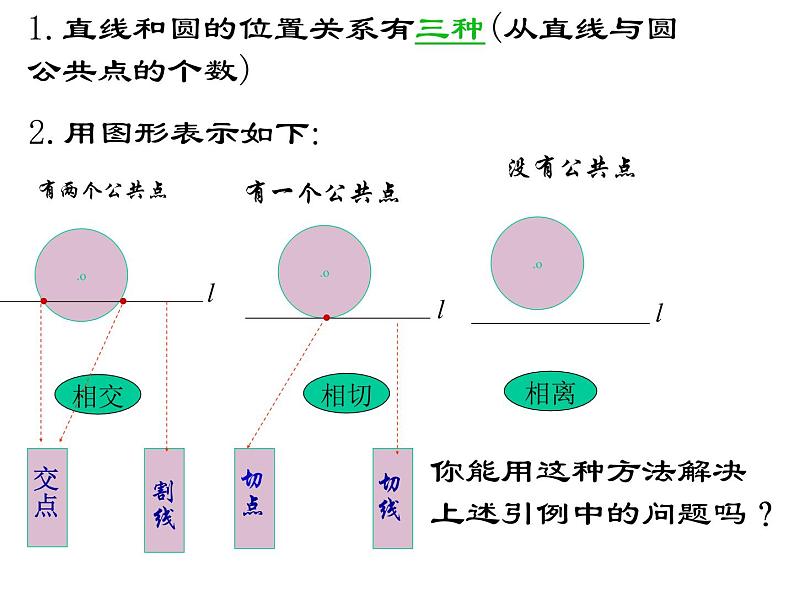
1.直线和圆的位置关系有三种(从直线与圆公共点的个数)
你能用这种方法解决上述引例中的问题吗？
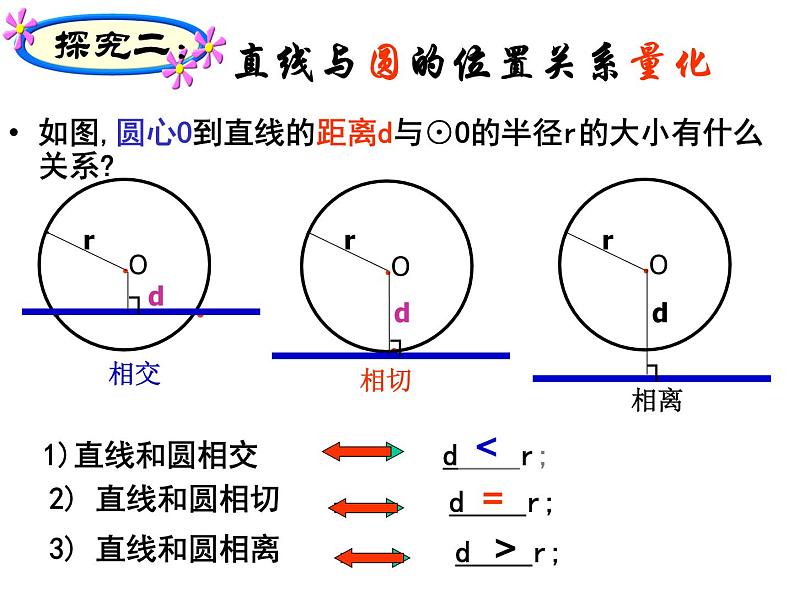
直线与圆的位置关系量化
如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系?
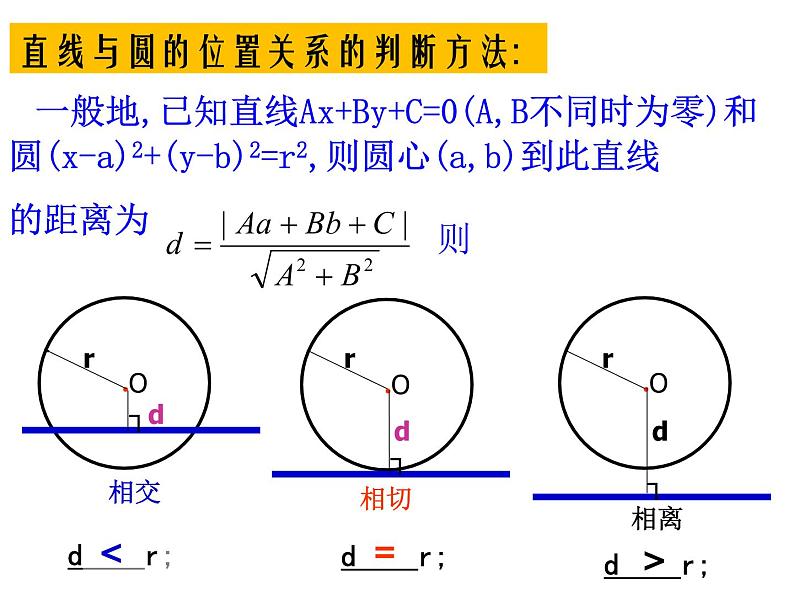
直线与圆的位置关系的判断方法:
一般地,已知直线Ax+By+C=0(A,B不同时为零)和圆(x-a)2+(y-b)2=r2,则圆心(a,b)到此直线的距离为
例1　判断下列各直线与圆的位置关系：
试一试：教材70页第1题
例2、一艘轮船在沿直线返回港口的途中，接到气象台的台风预报：台风中心位于轮船正西70km处，受影响的范围是半径长为30km的圆形区域。已知港口位于台风中心正北40km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？
解　⑴ 建立直角坐标系如图：由 已知可得 轮船所在位置坐标为（70，0），港口所在位置坐标为（0，40）。
圆心坐标为（0，0），半径为30
轮船航线所在的直线方程为：
圆心到轮船所在航线的距离为：
故这艘轮船不需改变航线，不会受到台风的影响。
过圆上一点的圆的切线有几条？
过圆外一点的圆的切线有几条？
解 设所求切线的斜率为k ，则切线方程为
所以圆心C(1，1) ，半径r=1．