高中数学6.1 数列的概念教学课件ppt

这是一份高中数学6.1 数列的概念教学课件ppt，共20页。PPT课件主要包含了有关青蛙的童谣，3中国奥运金牌数，一数列的定义，二数列的表示，三数列的分类，无穷数列，有穷数列，运用知识强化练习，an8-n，数列通项公式等内容，欢迎下载使用。
创设情景 引入概念
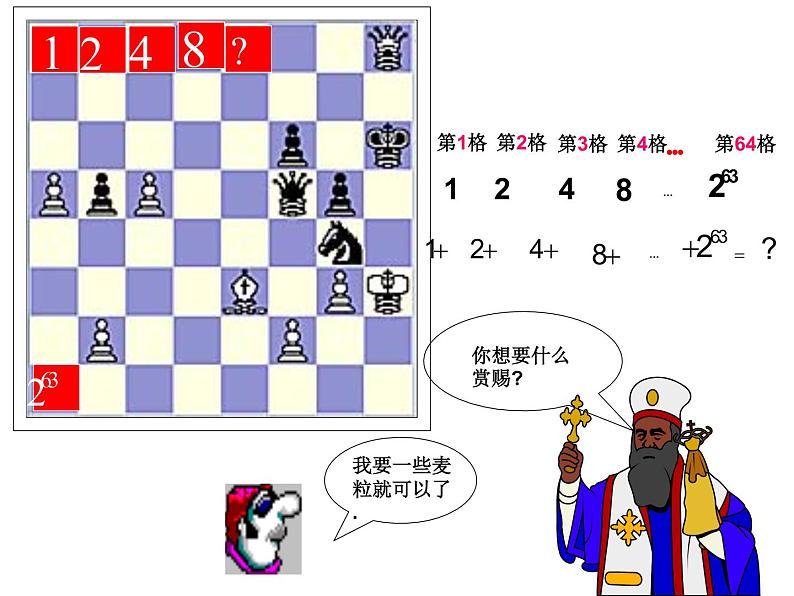
2麦粒数与国际象棋的故事
观察归纳 形成概念
数列—按照一定顺序排成的一列数
问题1：2,4,6,8 和 8,6,4,2是同一个数列吗?
不同，因为数的排列次序不同.
问题3：1,-1,1,-1,1,-1, 1, … 它是数列吗？
是， 数列中的数可以重复出现.
（1）数列中的数排列有序,数集中各元素排列无序；
问题4：数列和数集有什么区别?
（2）数列中的数可以重复出现,数集中各元素必须互异.
问题2: 王,后,车,象,马,兵. 它是一个数列吗?
不是，它不是由数构成.
讨论探究 深化概念
数列的项 _________________
数列的首项 _____________
(1) 2, 4, 6, 8, ……
数列的一般形式：a1，a2 ，a3 ，… , an …
或简记作{an }其中an是数列的第n项，叫做数列的通项
各项依次叫做这个数列的第1项，第2项，······，第n项， ······——项数
(1) 2,4,6,8,…
(2) 1,2,4,8,…,263
(4) 15,5,16,16,28,32,51
(5) 1,-1,1,-1,1,-1,…
按项的个数分
1.说出生活中的一个数列实例．
2.数列“1，2，3，4，5”与数列“5 ，4， 3，2，1 ”是否为同一个数列？
问题5：观察数列的每一项, 你发现数列的项an与其序号n有什么样的对应关系？这一关系用一个式子如何表示?
的第n项
之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式.
与序号
例2 根据下列各无穷数列的前4项,写出数列的一个通项公式.
(1)5,10,15,20，…；
解 （1）数列的前4项与其项数的关系如下表：
由此得到，该数列的一个通项公式为
解： (2) 数列前4项与其项数的关系如下表：
由此得到，该数列的一个通项公式为
(3) −1，1，−1，1，…．
解：（3）数列前4项与其项数的关系如下表：
例3 　判断16和45是否为数列{3n+1}中的项,如果是,请指出是第几项.
将45代入数列的通项公式有
练习 写出下面数列的一个通项公式，使它的前4项分别是下列各数。
练习 观察下面数列的特点，用适当的数填空，并写出一个通项公式.
(1) 2, 4, ( ), 16, 32, ( ), 128
(2) ( ), 4, 9, 16, 25,( ),49
即时训练 首尾呼应
根据引例中的数列，写出其通项公式