语文版（中职）基础模块下册10.9 一元线性回归课堂教学ppt课件

这是一份语文版（中职）基础模块下册10.9 一元线性回归课堂教学ppt课件，共60页。PPT课件主要包含了对于任意Xi值有，故回归方程为，引例分析，SST，SSE，SSR，自由度ƒR为1，图9-6，图9-7，图9-8等内容，欢迎下载使用。
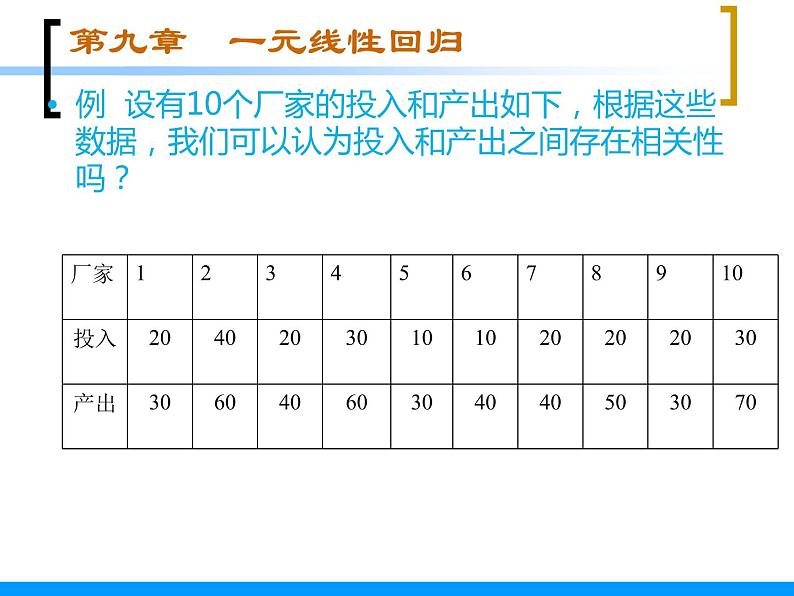
例 设有10个厂家的投入和产出如下，根据这些数据，我们可以认为投入和产出之间存在相关性吗？
9.1 回归分析的基本概念
9.1.1 因变量(Y)与自变量(X)之间的关系
根据因变量与自变量之间的关系不同，可以分为两种类型：
即对两个变量X，Y来说，当X值确定后，Y值按照一定的规律唯一确定，即形成一种精确的关系。
例：某商品的销售额y与销售量x之间的关系可表示为y=px(p是单价)，圆的面积可表示为s=piR^2
即当X值确定后，Y值不是唯一确定的，但大量统计资料表明，这些变量之间还是存在着某种客观的联系。
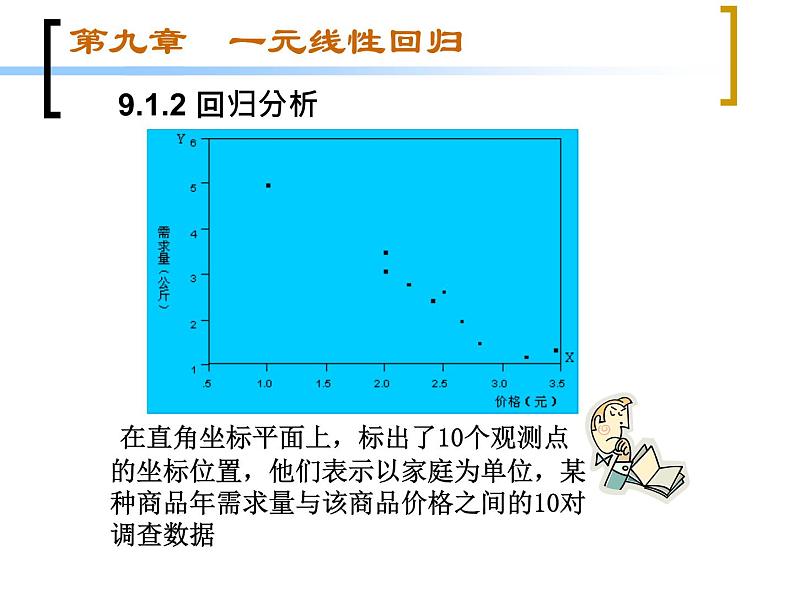
在直角坐标平面上，标出了10个观测点的坐标位置，他们表示以家庭为单位，某种商品年需求量与该商品价格之间的10对调查数据
回归分析(Regressin Analysis)
就是应用统计方法，对大量的观测数据进行整理、分析和研究，从而得出反映事物内部规律性的一些结论。
9.2 一元线性回归模型
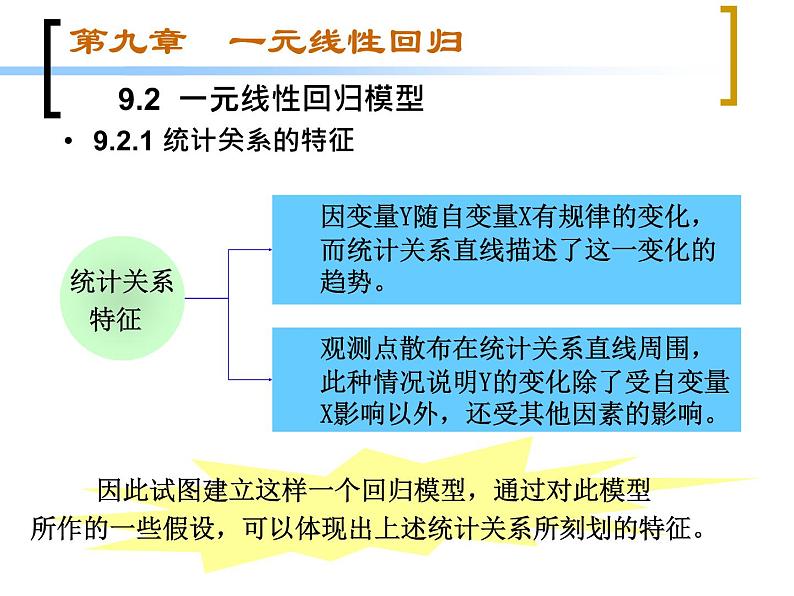
9.2.1 统计关系的特征
观测点散布在统计关系直线周围，此种情况说明Y的变化除了受自变量X影响以外，还受其他因素的影响。
因此试图建立这样一个回归模型，通过对此模型所作的一些假设，可以体现出上述统计关系所刻划的特征。
因变量Y随自变量X有规律的变化，而统计关系直线描述了这一变化的趋势。
9.2.2 一元线性回归模型假设
根据统计关系特征，可以进行下述假设：
(2)这些Y的概率分布的均值，有规律的随X变化而变化
(1)对于自变量的每一水平X，存在着Y的一个概率分布；
9.2.3 一元线性回归模型
Y与X具有统计关系而且是线性
Yi=β0+β1Xi+εi    (i=1,2,···,n) 
其中，(X i,Yj)表示(X,Y)的第i个观测值，β0 , β1为参数，β0+β1Xi为反映统计关系直线的分量，ε i为反映在统计关系直线周围散布的随机分量ε i～N (0,σ2)。
⑵E(Yi)=β0+β1Xi；
⑶
⑷各Yi间相互独立  Yi～N(β0+β1Xi,σ2) 。
9.2.4 一元线性回归方程
Y与X之间为线性关系
选出一条最能反映Y与X之间关系规律的直线
Yi=β0+β1Xi+εi β0和β1均未知
根据样本数据对β0和β1进行估计
β0和β1的估计值为b0和b1
建立一元线性回归方程
一般而言，所求的b0和b1应能使每个样本观测点(X i,Y i)与回归直线之间的偏差尽可能小，即使观察值与拟合值的误差平方和Q达到最小。
图9-4 回归方程原理图
令
Q达到最小值b0和b1称为最小二乘估计量
微积分中极值的必要条件
令偏导数为0
9.2.5 最小二乘估计量b0,b1的特性
表明b1是Yi的线性组合
可以证明b0和b1分别是β0和β1的无偏估计
真实值与预测值的差就是回归直线在每个给定点上的误差，我们称之为残差（residual）。
从几何上讲，残差是回归直线到样本数据点之间的垂直距离，确定斜率和截距的方程使回归直线位于样本点之间。这样，从回归直线到样本点之间的垂直距离相互抵消，使总和为0。
投入与产出例子中沿轴的残差分布
残差也用来确定异常点（utliers），异常点就是与其他点偏离，与总体趋势不符的数据点。异常点往往使残差幅度加大，在散点图中很容易识别。回归直线方程会受到计算中每个点的影响，因此，异常点的存在可能会使回归直线向异常点偏离。
回归方程的显著性检验（总体显著性检验）
9.3.1 总平方和分解
9.3.1 总平方和分解
图9-5 总平和分解图
它表示没有X的影响，单纯考察数据中Y的变动情况。
表示各 的变动程度，该变动是由于回归直线中各 Xi 的变动所引起的，并且通过X对Y的线性影响表现出来。
表示各Yi围绕所拟合的回归直线的变动程度
SST=SSR+SSE
SSE=SST-SSR
9.3.2 自由度的分解
自由度ƒ T为n-1
β0和β1用了两个正规方程
自由度ƒ E为n-2
自由度的分解可以表示为
n-1=1+（n-2）
9.3.3 回归均方与误差均方
9.4 样本确定系数与样本相关系数
9.4.1 样本确定系数
注:Y的总变差中能被X解释的那部分所占的比率
9.4.1 样本确定系数
样本的全部观察值都落在所拟和的回归直线上 SSE=0，
当X与Y无关，Y的变差完全由于随机因素引起，此时，SSR=0
9.4.2 样本相关系数
注:r与b1的分母均为正，分子相同,故r与b1有相同的符号。
平均投入220/10=22,平均产出450/10=45
9.5 一元线性回归显著性检验
在回归函数E(Y)=β0+β1X中，如果β1=0，则对于X的一切水平E(Y)=β0，说明Y的变化与X的变化无关，因而，我们不能通过X去预测Y。所以，对模型Yi=β0+β1Xi+εi  检验β1=0是否成立，等价于检验Y与X之间是否存在线性关系。
9.5.1 b1的抽样分布
为了检验β1=0是否成立，需要构造一个合适的统计量，因此，首先讨论b1的抽样分布。
b1是观测值Yi的线性组合
Yi服从正态分布且相互独立
且Yi相互独立，其中
在一元线性回归中，为了检验Y对于X线性关系的统计显著性，对β1进行F检验
1）提出假设：H0：β1=0，H1：β1≠0。
2） 构造并计算统计量：
3）查F分布临界值表，得临界值
4）比较： 接受H0，认为Y与X不存在一元线性关系。
拒绝H0，认为Y与X存在一元线性关系。
表9-1 方差分析表
9.5.3 t 检验
1）提出假设
H0: H1:
2）构造并计算统计量
3）查t分布临界值表
得临界值
若 ，接受H0
若 ，拒绝H0
查表得 ，落在了拒绝域，即自变量x与因变量y之间相关关系明显，投入量对产出量的影响显著。
9.5.4 利用样本相关系数进行统计检验
1）提出假设
H0:ρ =0H1:ρ
2）计算简单相关系数r
3）查相关系数临界值表
得临界值
ρ是总体Y与X的线性相关系数
9.5.4 利用样本相关系数进行统计检验
若 ，接受H0
若 ，拒绝H0
9.6 模型适合性分析
在对一元线性回归模型的适合性进行分析时,由于误差项是不可观测或测量的, 需借助残差的图像,来考察模型是否存在以下情况：异方差性和自相关性。
9.6.1 误差项的异方差性检验
若 不具有常数方差,称模型存在异方差性。此时,残差如下图所示，数据点呈现发散或收敛趋势。 在此种情况下,最小二乘法失效,因此需按照一定方法对数据进行变换。
误差项具有异方差性的残差图
9.6.2误差项的自相性关检验
如果观测值是来自一个时间序列的样本,则很可能出现误差项
是不独立的,将残差 et与时间t 作残
差图,将呈现出有规则的变化趋势。称模型存在自相关(Autcrrelatin)现象，也需按一定方法对数据进行修正。
9.6.2误差项的自相性关检验
误差项具有负自相关性的残差图