语文版（中职）拓展模块2.3 抛物线的标准方程和性质教案

这是一份语文版（中职）拓展模块2.3 抛物线的标准方程和性质教案，共5页。教案主要包含了复习，新知再现，典型例题，本节小结，当堂检测等内容，欢迎下载使用。
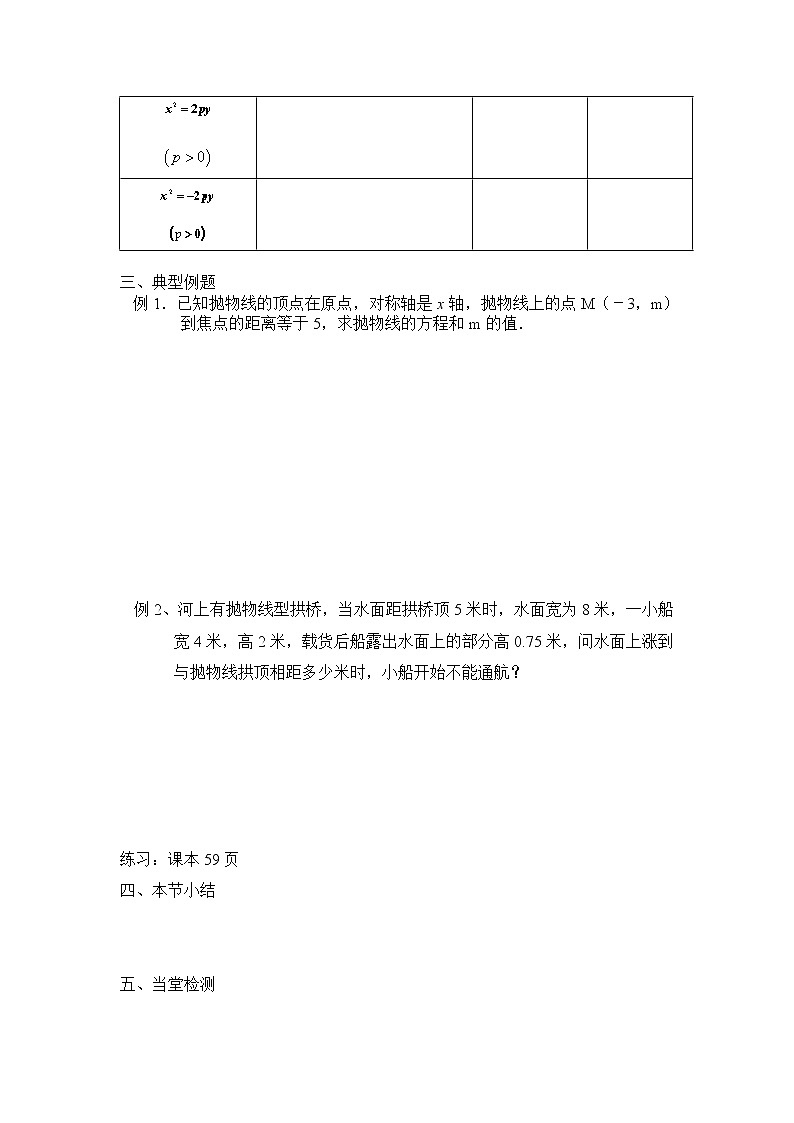
2.3.1抛物线及其标准方程学案班级________姓名_______学号_________学习目标：   1.掌握抛物线的定义及其标准方程；2.掌握抛物线的焦点、准线及其方程与焦点坐标的关系重点与难点：1、抛物线概念的形成；2、抛物线的标准方程的推导。学习过程：一、复习1.椭圆的定义：                          方程：                       双曲线的定义：                          方程：                   2．通过预习 根据下列条件写出抛物线的标准方程： (1)焦点是      （2）准线方程是       （3）焦点到准线的距离是2      (4)如果抛物线y 2=ax的准线是直线，那么它的焦点坐标为                       二、新知再现1．定义：平面内与一个定点F和一条定直线l 的距离相等的点的轨迹叫做             ，点F叫做抛物线的          ，直线l叫做抛物线的            。  2．抛物线的标准方程：                             新知探究：通过预习 抛物线的开口方向还有几种情况？你能得出它们的方程吗？在学生探究的基础上，完成下表：标准方程图形焦点准线          三、典型例题例1．已知抛物线的顶点在原点，对称轴是x轴，抛物线上的点M（－3，m）到焦点的距离等于5，求抛物线的方程和m的值．            例2、河上有抛物线型拱桥，当水面距拱桥顶5米时，水面宽为8米，一小船宽4米，高2米，载货后船露出水面上的部分高0.75米，问水面上涨到与抛物线拱顶相距多少米时，小船开始不能通航？     练习：课本59页四、本节小结  五、当堂检测 1．一抛物线形拱桥，当水面离桥顶2m时，水面宽4m，若水面下降1m，则水面宽为                        2．抛物线的顶点在原点，对称轴是x轴，抛物线上点（-5，m）到焦点距离是6，则抛物线的           方程是                       3．抛物线的焦点为椭圆的左焦点，顶点在椭圆中心，则抛物线方程     2.3.2抛物线的简单几何性质学习目标1．能叙述抛物线的简单几何性质，如范围、对称性、顶点和离心率等;2．能用抛物线的简单几何性质解决一些简单问题;3．能在对抛物线几何性质的讨论中，体会数形结合的思想与转化。学习重点、难点重点：抛物线的几何性质及初步运用;难点：抛物线的几何性质及初步运用。学习过程：一、温故知新：在直角坐标系中，顶点在原点，轴与坐标轴重合的共有四种情况，因此抛物线的方程相应也有四种形式，它们都叫抛物线的标准方程。1、  抛物线定义：（根据表格中信息填空）                                                                                                                                                                                                                                                        抛物线方程抛物线的图像抛物线的焦点坐标抛物线的准线方程             总结：1、抛物线的开口方向取决于_________________________________;2、抛物线的焦点在哪个轴上取决于___________________________; 3、在同一坐标系中画出下列抛物线的草图：（1）        （2）         （3）说明抛物线的开口大小取决于___________________________________。二、新知探究：以为例来研究1、对称性：抛物线关于____________对称，只有____________条对称轴。2、范围：抛物线的图像在____________，开口向____________，该图像向_______________________________无限延伸，抛物线是____________。3、顶点：抛物线的顶点是____________。4、离心率：由定义可知，抛物线的离心率e=____________。5、抛物线的通径：____________。它的几何意义是_______________________________。三、合作探究 填写下表（用类比的方法）：设焦点到准线的距离为P(P>0)  图像     标准方程范围     对称轴     顶点     离心率        焦点坐标     准线方程     四、典型例题：1、求顶点在原点，通过点，且以坐标轴为轴的抛物线的标准方程。   2（课本例4）、斜率为1的直线l经过抛物线的焦点，且与抛物线相交于A、B两点，求线段AB的长。    3（课本例5）、已知抛物线的方程为，直线l过定点P（-2,1），斜率为k，当k为何值时，直线l与抛物线：只有一个公共点；有两个公共点；没有公共点。    五、当堂检测1.已知抛物线的顶点在原点，焦点在轴上，抛物线上一点到焦点的距离为5，求的值、抛物线的标准方程和准线方程。   2.若直线经过抛物线的焦点，则实数=________________.