高中第二单元 椭圆、双曲线、抛物线2.1 椭圆的标准方程和性质背景图ppt课件

这是一份高中第二单元 椭圆、双曲线、抛物线2.1 椭圆的标准方程和性质背景图ppt课件，共30页。PPT课件主要包含了仙女座星系，星系中的椭圆，椭圆的定义，讲授新课，ab0，a＞b＞0，椭圆的标准方程，则椭圆方程为，椭圆方程的几何意义，b2a2c2等内容，欢迎下载使用。
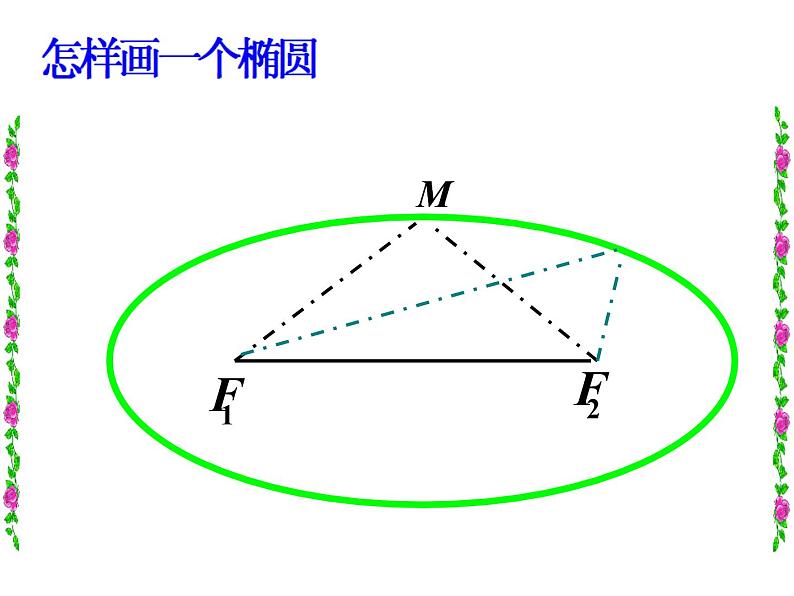
平面内与两个定点F1、F2的距离的和等于常数（大于|F1F2|）的点的轨迹叫做椭圆，
这两个定点叫做椭圆的焦点(F1、F2 )，
两焦点的距离叫做椭圆的焦距|F1F2|.
平面内到两个定点F1、F2的距离之和等于常数（大于|F1F2|）的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。
1、F1、F2是两个不同的点；
2、M是椭圆上任意一点，且|MF1| + |MF2| = 常数；
3、通常这个常数记为2a，焦距记为2c，且2a>2c；
4、如果2a = 2c，则M点的轨迹是线段F1F2.
5、如果2a < 2c，则M点的轨迹不存在.（由三角形的性质知）
随堂练习.用定义判断下列动点M的轨迹是否为椭圆。
(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。
(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。
(4)到F1(-2,0)、F2(0,2)的距离之和为3的点的轨迹。
因|MF1|+|MF2|=6>|F1F2|=4，故点M的轨迹为椭圆。
因|MF1|+|MF2|=4=|F1F2|=4，故点M的轨迹不是椭圆 (是线段F1F2)。
(3)到F1(0,-2)、F2(0,2)的距离之和为3的点的轨迹。
因|MF1|+|MF2|=4＜|F1F2|=4，故点M的轨迹不存在。
如图，建立直角坐标系xOy，
使x轴经过点F1、F2，并且
点O与线段F1F2的中点重合.
设点M(x, y)是椭圆上任一点，
椭圆的焦距为2c(c＞0).
焦点F1、F2的坐标分别是 (－c, 0)、(c, 0)．
又设M与F1和F2的距离的和等于常数2a．
|MF1|＋|MF2|＝2a
2. 椭圆标准方程的推导：
如图所示： F1、F2为两定点，且|F1F2|=2c，求平面内到两定点F1、F2距离之和为定值2a（2a>2c)的动点M的轨迹方程。
解：以F1F2所在直线为X轴， F1F2 的中点为原点建立平面直角坐标系，则焦点F1、F2的坐标分别为(-c,0)、 (c,0)。
设M（x,y)为所求轨迹上的任意一点，
则:|MF1|+ |MF2|=2a
两边平方得：a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2
即：(a2-c2)x2+a2y2=a2(a2-c2)
因为2a>2c，即a>c，所以a2-c2>0，令a2-c2=b2，其中b>0，代入上式可得：
b2x2+a2y2=a2b2
两边同时除以a2b2得：
这个方程叫做椭圆的标准方程，它所表示的椭圆的焦点在x 轴上。
是F1(c, 0)、F2(－c, 0)，且c2＝a2－b2.
它所表示的椭圆的焦点在x轴上，焦点
如果使点F1、F2在y轴上，点F1、F2的坐标是F1(0,－c)、F2(0, c)，
如何根据标准方程判断焦点在哪个坐标轴上？
两种形式的标准方程的比较：
|MF1|+|MF2|=2a (2a>|F1F2|)
(c,0)、(c,0)
(0,c)、(0,c)
分母哪个大，焦点就在哪一根坐标轴上
答:在 x 轴上(-3,0)和(3,0）
答:在 y 轴上(0,-5)和(0,5）
答:在y 轴上(0,-1)和(0,1)
焦点在分母大的那个轴上。
判定下列椭圆的焦点在 哪个轴上，写出焦点坐标。
写出适合下列条件的椭圆的标准方程
(1) a =4，b=1，焦点在 x 轴上； (2) a =4，b=1，焦点在坐标轴上；
例、椭圆的两个焦点的坐标分别是(－4, 0 )、( 4 , 0 )，椭圆上一点P到两焦点距离之和等于10,求椭圆的标准方程。
解： ∵椭圆的焦点在x轴上∴设它的标准方程为:∵ 2a=10, 2c=8∴ a=5, c=4∴ b2=a2－c2=52－42=9∴所求椭圆的标准方程为:
5：若方程4x2+ky2=1表示的曲线是焦点在y轴上的椭圆，求k的取值范围。
∵方程表示的曲线是焦点在y轴上的椭圆
∴k的取值范围为0