高中数学3.3 古典概率课前预习ppt课件

这是一份高中数学3.3 古典概率课前预习ppt课件，共39页。PPT课件主要包含了则该试验的样本空间，如i2，PA具有如下性质，n-1，n-2，n-k+1，种取法，故抽签与顺序无关，可通过该试验计算π，推广的加法定理等内容，欢迎下载使用。
例如，一个袋子中装有10个大小、形状完全相同的球，将球编号为1－10。把球搅匀，蒙上眼睛，从中任取一球。因为抽取时这些球是完全平等的，我们没有理由认为10个球中的某一个会比另一个更容易取得。也就是说，10个球中的任一个被取出的机会是相等的，均为1/10。
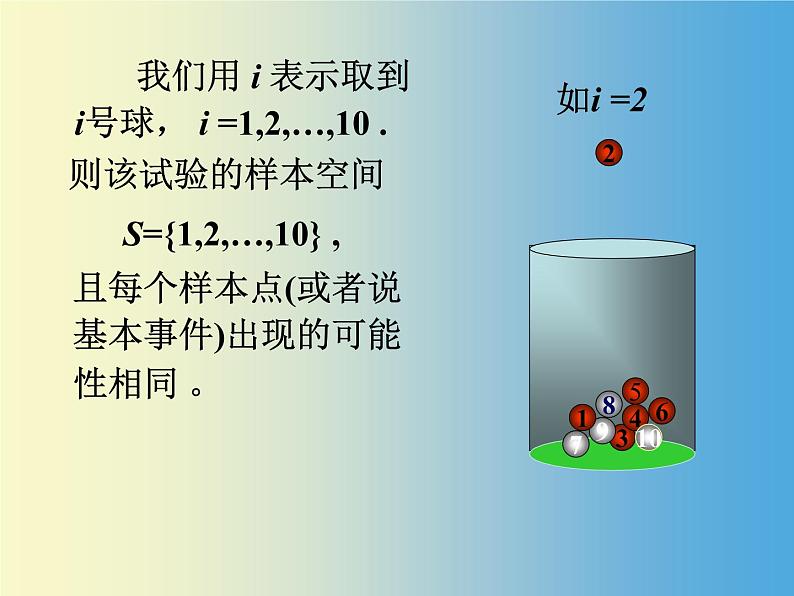
我们用 i 表示取到 i号球， i =1,2,…,10 .
且每个样本点(或者说基本事件)出现的可能性相同 。
S={1,2,…,10} ,
设试验的样本空间共有N个等可能的基本事件，其中有且仅有M个基本事件包含于随机事件A，则A的概率为：
(1) 0 P(A) 1；(2) P()＝1； P( )=0
古典概型中的概率(概率的古典定义):
例:有三个子女的家庭,设每个孩子是男是女的概 率相等,则至少有一个男孩的概率是多少? 解:设A--至少有一个男孩,以H表示某个孩子是男孩
N={HHH,HHT,HTH,THH,HTT,TTH,THT,TTT}
M={HHH,HHT,HTH,THH,HTT,TTH,THT}
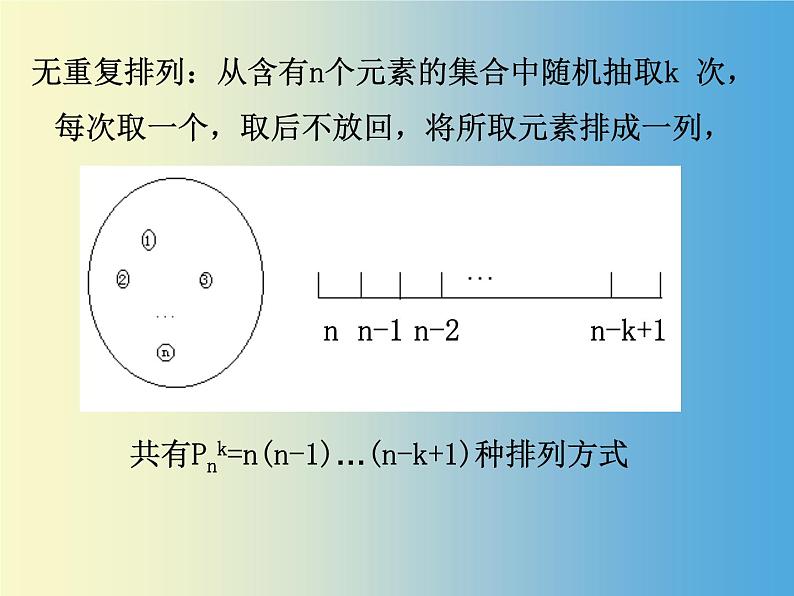
无重复排列：从含有n个元素的集合中随机抽取k 次，每次取一个，取后不放回，将所取元素排成一列，
共有Pnk=n(n-1)…(n-k+1)种排列方式
组合：从含有n个元素的集合中随机抽取k个，共有
抽球问题 例:设盒中有3个白球，2个红球，现从盒中任抽2个球，求取到一红一白的概率。解:设A表示取到一红一白
答:取到一红一白的概率为0.6
一般地，设盒中有N个球，其中有M个白球，现从中任抽n个球，则这n个球中恰有k个白球的概率是
在实际中，产品的检验、疾病的抽查、农作物的选种等问题均可化为随机抽球问题。我们选择抽球模型的目的在于问题的数学意义更加突出，而不必过多地交代实际背景。
练习：1、袋中有4个白球、6个红球，从中随机取4个，求取到2白2红的概率。2、10个钉子中有三个是坏的，随机抽取4个，求（1）恰有2个是坏的（2）4个全是好的的概率。
*分组问题例：30名学生中有3名运动员，将这30名学生平均分成3组，求：（1）每组有一名运动员的概率；（2）3名运动员集中在一个组的概率。解:设A:每组有一名运动员;B: 3名运动员集中在一组
一般地，把n个球随机地分成m组(n>m),要求第 i 组恰有ni个球(i=1,…m)，共有分法：
练习：20名运动员中有2名种子选手，现将运动员平分成2组，问2名种子选手（1）分在不同组（2）分在同一组的概率。略解：
例：袋中装有1、2、……N号球各1只，采用（1）有放回（2）无放回方式摸球，每次摸1球，求第k次首次摸到1号球的概率。解：
例：袋中有a只白球与b只黑球，除颜色不同其它方面无差别，现在把球随机地一只只摸出来，求第k次摸出的球是白球的概率。分析：把a只白球与b只黑球看作是不同的，对它们进行编号，若把摸出的球依次放在排列成一直线的a+b个位置上，则可能的排法为(a+b)!，把它们作为样本点全体，第k次摸得白球有a种取法，而另外(a+b-1)次摸球相当于对a+b-1只球进行全排列。解：
例：一部四本头的文集按任意次序放在书架上，问各册自右向左或自左向右恰成1、2、3、4顺序的概率。解：
例：将3个球随机放入4个杯子，问杯中球的最大个数分别是1、2、3的概率。解：设Bi（i=1、2、3）表示杯中球的最大个数为i
例:设有n个球,每个都以相同的概率1/N落到N个格子中(N大于等于n)，试求（1）指定的n个格子中各有一球（2）任何n个格子中各有一球（3）某指定的一个格子中恰有k个球（4）恰好n-1个格子里有球解：（1）由于每个球可N个格子中的任一个，所以共有Nn种可能
（3）由于在n个球中选出k个有Cnk种选法，而其余的n-k个球可任意放在N-1个格子中，这种放法有（N-1）n-k种
（4）这意味着一个格子有2个球，而另n-2个格子内各有1球，可先任取落入2个球的一个格子，有N种取法，再任取落入1个球的n-2个格子，有CN-1n-2种取法，最后将球落进去。
概率论历史上著名问题：求参加某次集会的n 个人(n365)中没有两个人的生日在同一天的概率。
把n个人看作上面问题中的n个球，把一年的365天作为格子，则N=365，现在我们假设n=40，则
没有两人生日相同的概率竟然是意外的小！
例：从n双不同的鞋子中任取2r（2rb，在AC上随机取一点x，在CB上随机取一点y，求AX、XY、YB可构成三角形的概率。解：设线段AX、YB长度分别为x，y，则XY长度为a+b-x-y， 0≤x≤a，0≤y≤b，为构成三角形必须：x