（3）空间向量与立体几何——2022届新高考数学解答题专练

这是一份（3）空间向量与立体几何——2022届新高考数学解答题专练，共18页。试卷主要包含了如图所示等内容，欢迎下载使用。
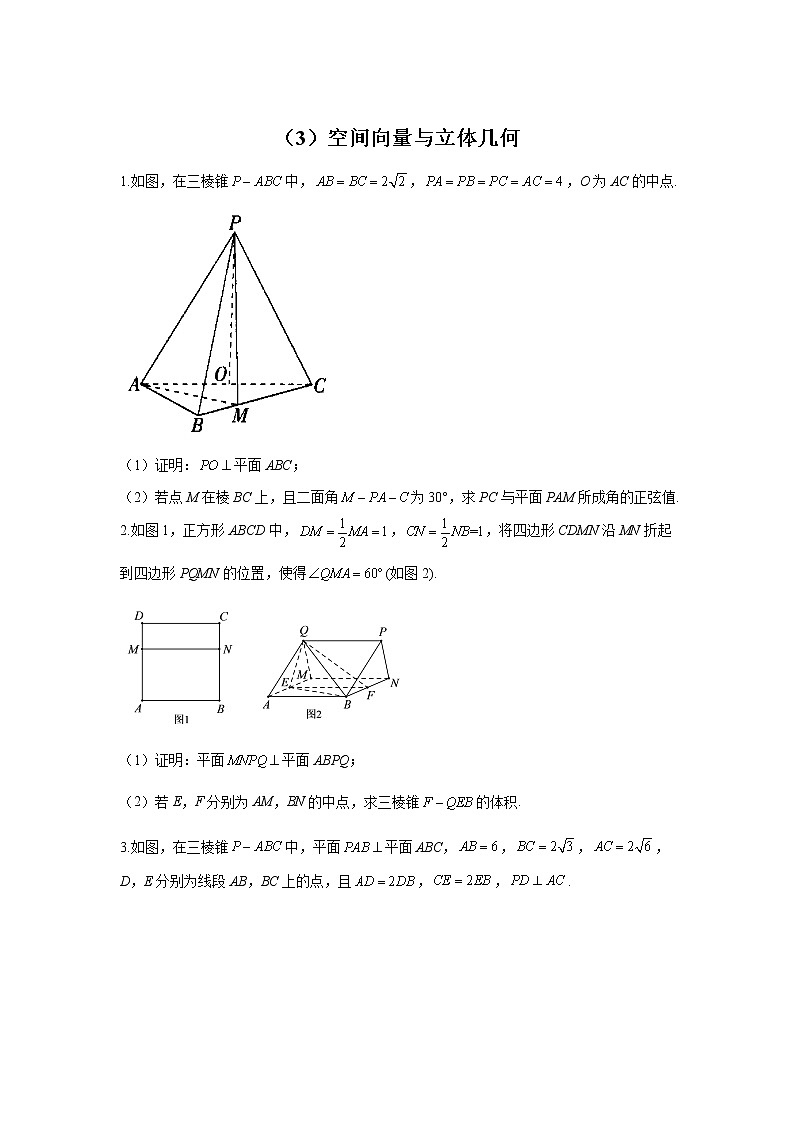
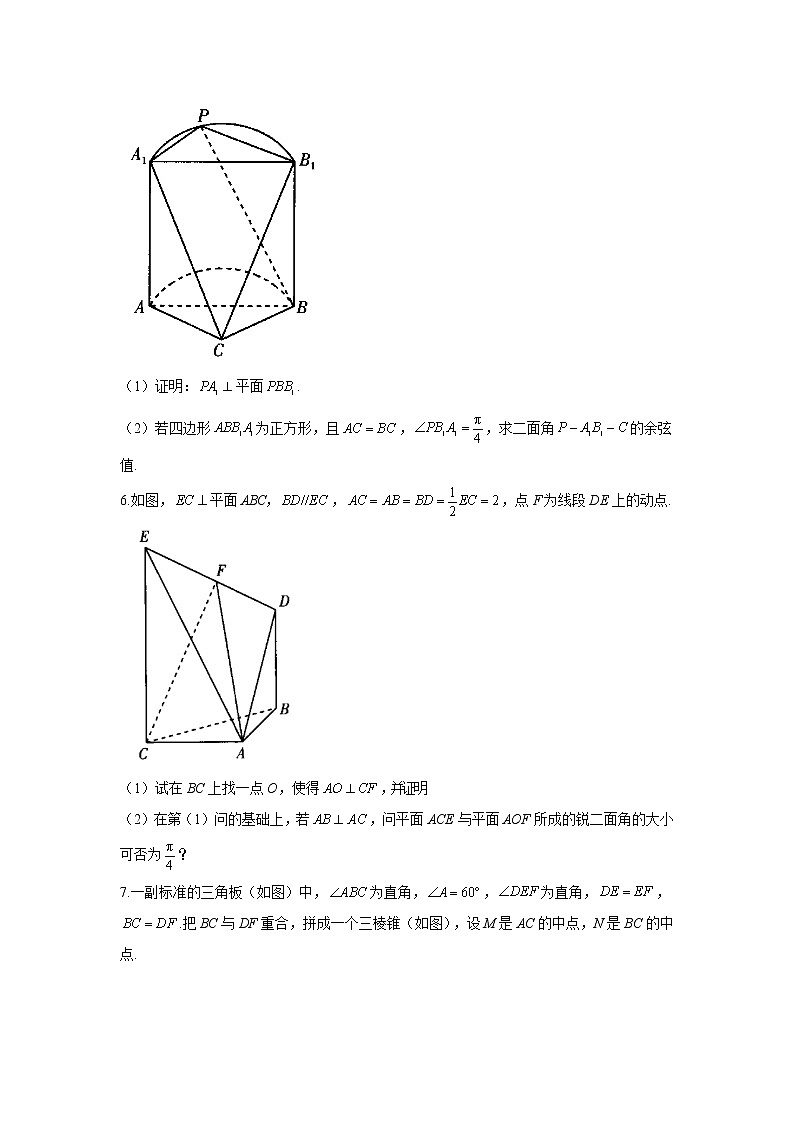
 （3）空间向量与立体几何1.如图，在三棱锥中，，，O为AC的中点.（1）证明：平面ABC；（2）若点M在棱BC上，且二面角为30°，求PC与平面PAM所成角的正弦值.2.如图1，正方形ABCD中，，，将四边形CDMN沿MN折起到四边形PQMN的位置，使得(如图2).（1）证明：平面平面ABPQ；（2）若E，F分别为AM，BN的中点，求三棱锥的体积.3.如图，在三棱锥中，平面平面ABC，，，，D，E分别为线段AB，BC上的点，且，，.（1）求证：平面ABC；（2）若直线PA与平面ABC所成的角为，求平面PAC与平面PDE所成的二面角的大小.4.已知几何体，如图所示，其中四边形、四边形、四边形均为正方形，且边长均为1，点在棱上.(1)求证：.(2)是否存在点，使得直线与平面所成的角为45°？若存在，确定点的位置；若不存在，请说明理由.5.如图是一个半圆柱与多面体构成的几何体，平面ABC与半圆柱的下底面共面，且，P为上的动点(不与，重合).（1）证明：平面.（2）若四边形为正方形，且，，求二面角的余弦值.6.如图，平面ABC，，，点F为线段DE上的动点.（1）试在BC上找一点O，使得，并证明.（2）在第（1）问的基础上，若，问平面ACE与平面AOF所成的锐二面角的大小可否为？7.一副标准的三角板（如图）中，为直角，，为直角，，.把BC与DF重合，拼成一个三棱锥（如图），设M是AC的中点，N是BC的中点.（1）求证：平面平面EMN.（2）若，二面角为直二面角，求直线EM与平面ABE所成角的正弦值.8.如图（1），已知圆O的直径AB的长为2，上半圆圆弧上有一点C，，点P是弧AC上的动点，点D是下半圆弧的中点.现以AB为折痕，使下半圆所在的平面垂直于上半圆所在的平面，连接PO，PD，PC，CD，如图（2）所示.（1）当平面PCD时，求PC的长；（2）当三棱锥体积最大时，求二面角的余弦值.9.如图（1），AD是中BC边上的高，且，将沿AD翻折，使得平面平面ABD，如图（2）所示.（1）求证：.（2）在图（2）中，E是BD上一点，连接AE，CE，当AE与底面ABC所成角的正切值为时，求直线AE与平面BCE所成角的正弦值.10.如图，正方形ABCD和ABEF所在的平面互相垂直，且边长都是1，M，N，G分别为线段AC，BF，AB上的动点，且，平面MNG，记.（1）证明：平面ABEF.（2）当MN的长度最小时，求二面角的余弦值.  答案以及解析1.答案：(1)证明过程见解析.(2)PC与平面PAM所成角的正弦值为.解析：(1)证明：因为，O为AC的中点，所以，且.连接OB.因为，所以为等腰直角三角形，且，.由知.由，，知平面ABC.（2）如图，以O为坐标原点，的方向为x轴正方向，建立空间直角坐标系Oxyz.由题意得，，，，，.易得平面PAC的一个法向量为.设，则.设平面PAM的法向量为.由，，得可取，所以.由已知可得，所以，解得（舍去）或，所以.又，所以.所以PC与平面PAM所成角的正弦值为.2.答案：(1)见解析(2)解析：(1)在正方形ABCD中，，，，，又，在中，由余弦定理得，，，，又，平面ABPQ，平面ABPQ，又平面MNPQ，平面平面ABPQ；(2)由(1)知，，在正方形ABCD中，，，四边形CDMN为矩形，，，，，，MQ、平面AMQ，平面AMQ，平面ABNM，平面平面AMQ，过Q作于H，则平面ABNM，即平面BEF，，.3.答案：(1)见解析(2)解析：(1)因为，，，所以，所以，可得，又因为，所以，可得，又因为，所以，所以，因为平面平面ABC，平面平面，面ABC，所以平面PAB，因为面PAB，所以，因为，，所以平面ABC.(2)由(1)知DC，DB，DP两两垂直，如图分别以DC，DB，DP所在的直线为x，y，z轴建立空间直角坐标系，因为直线PA与平面ABC所成的角为，即，所以，则，，，，所以，，，因为，，所以，由(1)知，所以，又平面ABC，面ABC，所以，因为，所以平面PDE，所以为平面PDE的一个法向量，设平面PAC的法向量为，由，令，得，，所以为平面PAC的一个法向量.所以，所以平面PAC与平面PDE所成的锐二面角的余弦值为，故平面PAC与平面PDE所成的锐二面角为.4.答案：(1)证明过程见解析.(2)存在点M使得直线MB与平面BEF所成的角为45°.解析：(1)四边形ABCD、四边形CDGF、四边形ADGE均为正方形，，.又，平面ABCD.以点D为坐标原点，建立如图所示的空间直角坐标系，则，，.点在棱上，故可设.，，，.(2)假设存在点M，使得直线MB与平面BEF所成的角为45°.设平面的法向量为，，，，，令，得为平面BEF的一个法向量，.直线与平面所成的角为45°，，解得.又.存在点.当点M位于棱DG上，且时，使得直线MB与平面BEF所成的角为45°.5.答案：（1）见解析（2）解析：（1）在半圆柱中，平面，平面，所以.因为是上底面对应圆的直径，所以.因为，平面，平面，所以平面.（2）根据题意，以C为坐标原点建立空间直角坐标系，如图所示.设，则，，，所以，.易知为平面的一个法向量.设平面的法向量为，则即令，则，，所以为平面的一个法向量.所以.由图可知二面角为钝角，所以所求二面角的余弦值为.6.答案：（1）BC的中点即为所找的点O.理由见解析.（2）当F为DE的中点时，平面ACE与平面AOF所成的锐二面角的大小为解析：（1）BC的中点即为所找的点O.，，又平面ABC，平面ABC，.，平面BDEC，平面BDEC，平面BDEC.又平面BDEC，.（2）以A为坐标原点，AB，AC所在直线分别为x轴、y轴，过点A且平行于EC的直线为z轴建立如图所示的空间直角坐标系，则，，，，，.设，则可得，则.设平面AOF的法向量为，则即令，则，，则为平面AOF的一个法向量.易得平面ACE的一个法向量为.令，解得.故当F为DE的中点时，平面ACE与平面AOF所成的锐二面角的大小为.7.答案：（1）见解析（2）解析：（1）是AC的中点，N是BC的中点，，，.，N是BC的中点，.又，平面EMN，平面EMN，平面EMN.又平面ABC，平面平面EMN.（2）由（1）可知，，，为二面角的平面角，又二面角为直二面角，，即.以点N为坐标原点，NM，NC，NE所在直线分别为x，y，z轴建立如图所示的空间直角坐标系，，，，，，则，，，，，，，.设为平面ABE的法向量，则即得，令，则，平面ABE的一个法向量为.设直线EM与平面ABE所成的角为，则，即直线EM与平面ABE所成角的正弦值为.8.答案：（1）（2）解析：（1）因为平面PCD，平面OCP，平面平面，所以.又，所以.又，所以为正三角形，所以.（2）由题意知平面COP，而，，所以当时，三棱锥的体积最大.解法一  易知OP，OD，OC两两垂直，以O为坐标原点，，，的方向分别为x轴、y轴、z轴的正方向，建立如图所示的空间直角坐标系，则，，，，.设平面DPC的法向量为，则即取，得平面DPC的一个法向量为.易知平面PCO的一个法向量为，设二面角的平面角为，由题图知，二面角的平面角为锐角，则，所以二面角的余弦值为.解法二  如图所示，取PC的中点H，连接OH，DH.因为，，所以OH，DH都与PC垂直，即为所求二面角的平面角.在中，可得，在中，，所以，所以二面角的余弦值为.9.答案：（1）见解析（2）解析：（1）由题图（1）知，在题图（2）中，，.平面平面ABD，平面平面，平面ABD，平面ACD，又平面ACD，.（2）以A为坐标原点，AC，AB，AD所在的直线分别为x，y，z轴建立如图所示的空间直角坐标系，不妨设，则，，，，，，.设，由，得，得，，又平面ABC的一个法向量为，AE与底面ABC所成角的正切值为，所以，于是，即，解得，则，，.设平面BCE的法向量为，则即令，得，，则是平面BCE的一个法向量，设直线AE与平面BCE所成的角是，则，故直线AE与平面BCE所成角的正弦值为.10.答案：（1）见解析（2）解析：（1）因为平面MNG，且平面ABEF，平面平面，所以，所以，所以，所以，所以，所以.又平面平面ABEF，且平面ABCD，平面平面，所以平面ABEF.（2）由（1）知，，，，所以，当且仅当时等号成立，即当时，MN的长度最小.以B为坐标原点，分别以BA，BE，BC所在的直线为x轴、y轴、z轴建立如图所示的空间直角坐标系，则，，，，设平面AMN的法向量为，因为，，所以取，得为平面AMN的一个法向量.设平面BMN的法向量为，因为，，所以取，得为平面BMN的一个法向量.所以，又二面角为钝二面角，所以二面角的余弦值为.