

吉林省长春市绿园区2021-2022学年八年级上学期期末考试数学试题(word版 含答案)
展开2021-2022学年吉林省长春市绿园区八年级第一学期期末数学试卷
一、选择题(本大题共8小题,每小题3分,共24分)
1.﹣8的立方根是( )
A.4 B.2 C.﹣2 D.±2
2.下列数是无理数的是( )
A. B.π C.0 D.
3.计算(x2)3的结果是( )
A.x5 B.x6 C.x8 D.3x2
4.计算的结果为( )
A.10 B.5 C.3 D.2
5.运用乘法公式计算(4+x)(x﹣4)的结果是( )
A.x2﹣16 B.x2+16 C.16﹣x2 D.﹣x2﹣16
6.如图所示,在△ABC中,∠ACB=90°,分别以AB、BC、AC为边向外作正方形,若三个正方形的面积分别为225、400、S,则S的值为( )
A.25 B.175 C.600 D.625
7.如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
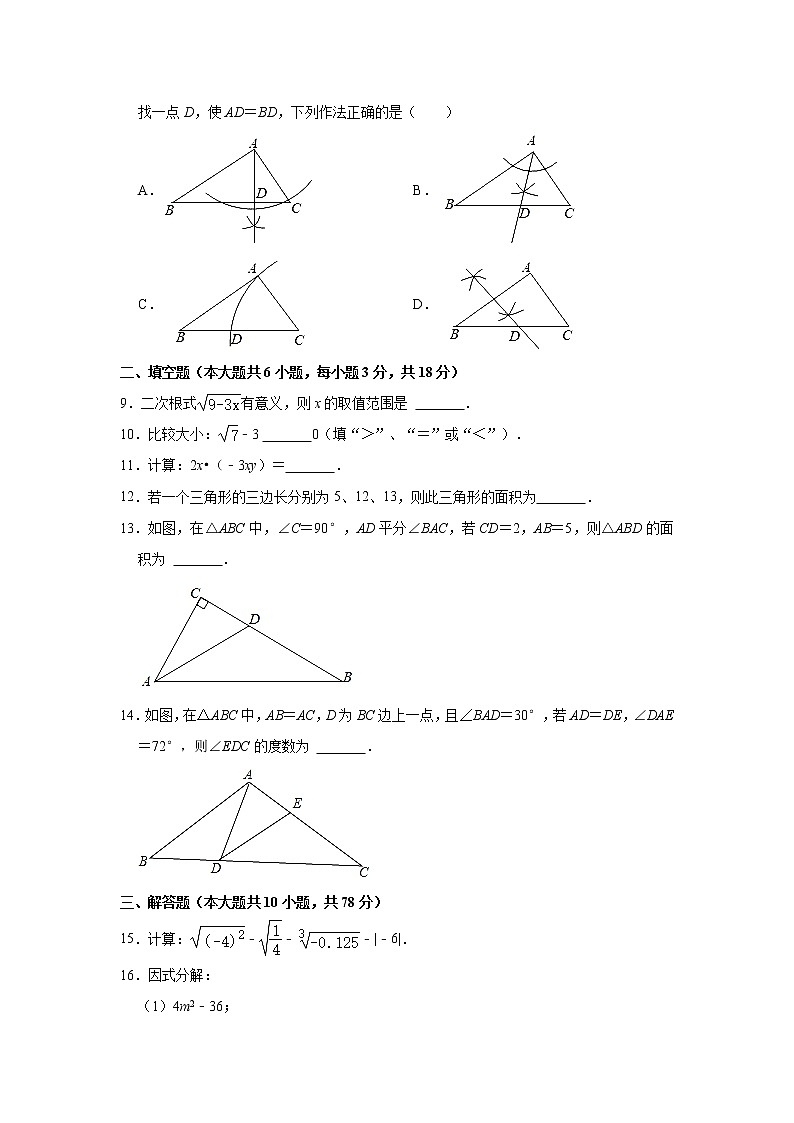
8.在△ABC中,∠BAC=90°,AB>AC,∠B≠30°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
9.二次根式有意义,则x的取值范围是 .
10.比较大小:﹣3 0(填“>”、“=”或“<”).
11.计算:2x•(﹣3xy)= .
12.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,若CD=2,AB=5,则△ABD的面积为 .
14.如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠DAE=72°,则∠EDC的度数为 .
三、解答题(本大题共10小题,共78分)
15.计算:﹣﹣﹣|﹣6|.
16.因式分解:
(1)4m2﹣36;
(2)2a2b﹣8ab2+8b3.
17.图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长均为1,点A、点B均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图①中,以线段AB为腰画一个等腰三角形.
(2)在图②中,以线段AB为底画一个等腰三角形.
18.先化简,再求值:(x﹣3)2﹣x(2x+1)+x2,其中x=.
19.如图,点B、F、C、E四点在同一条直线上,∠B=∠E,AB=DE,BF=CE.求证:AC=DF.
20.如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东40°方向航行,乙船沿南偏东50°方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少?
21.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形.
(1)图2中间空白的部分的面积是 ;
(2)观察图2,请你写出代数式(a+b)2、(a﹣b)2、ab之间的等量关系式 ;
(3)根据你得到的关系式解答下列问题:若x+y=﹣4,xy=3,求x﹣y的值.
22.2021年央视春晚,数十个节目给千家万户送上了丰富的“年夜大餐”.某校随机对八年级部分学生进行了一次调查,对最喜欢相声《年三十的歌》(记为A)、歌曲《牛起来》(记为B)、武术表演《天地英雄》(记为C)、小品《开往春天的幸福》(记为D)的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:
(1)求本次接受调查的学生人数.
(2)求扇形统计图中D所在扇形的圆心角度数.
(3)将条形统计图补充完整.
23.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图(1)的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系.
24.如图,在Rt△ABC中,∠ABC=90°,BC=AB,AC=8,点D是边AC的中点,动点P从点D出发,沿DA以每秒2个单位长度的速度向终点A匀速运动.同时,动点Q从点D出发,沿DC以每秒1个单位长度的速度向终点C匀速运动.当点P到达终点时,点Q也随之停止运动.过点Q作QE⊥AC,使QE=QD,且点E落在直线AC的上方,当点P不与点D重合时,以PQ、QE为邻边作长方形PQEF.设长方形PQEF与△ABC的重叠部分的面积为S,点P的运动时间为t(秒).
(1)用含t的代数式表示线段AP的长度为 .
(2)当点F落在线段AB上时,求t的值.
(3)用含t的代数式表示S.
(4)连结AF、DF.当△AFD是等腰三角形时,直接写出t的值.
参考答案
一、选择题(本大题共8小题,每小题3分,共24分)
1.﹣8的立方根是( )
A.4 B.2 C.﹣2 D.±2
【分析】根据立方根的定义即可求解.
解:﹣8的立方根是﹣2.
故选:C.
2.下列数是无理数的是( )
A. B.π C.0 D.
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解:A.是分数,属于有理数,故本选项不合题意;
B.π是无理数,故本选项符合题意;
C.0是整数,属于有理数,故本选项不合题意;
D.,是整数,属于有理数,故本选项不合题意;
故选:B.
3.计算(x2)3的结果是( )
A.x5 B.x6 C.x8 D.3x2
【分析】根据幂的乘方和积的乘方的运算法则求解.
解:(x2)3=x6.
故选:B.
4.计算的结果为( )
A.10 B.5 C.3 D.2
【分析】直接利用二次根式的乘法运算法则计算得出答案.
解:=5.
故选:B.
5.运用乘法公式计算(4+x)(x﹣4)的结果是( )
A.x2﹣16 B.x2+16 C.16﹣x2 D.﹣x2﹣16
【分析】用平方差公式直接得出结果.
解:(4+x)(x﹣4)
=(x+4)(x﹣4)
=x2﹣42
=x2﹣16,
故选:A.
6.如图所示,在△ABC中,∠ACB=90°,分别以AB、BC、AC为边向外作正方形,若三个正方形的面积分别为225、400、S,则S的值为( )
A.25 B.175 C.600 D.625
【分析】由勾股定理得:AC2+BC2=AB2,直接代入即可.
解:在△ABC中,∠ACB=90°,
由勾股定理得:AC2+BC2=AB2,
∴225+400=S,
∴S=625.
故选:D.
7.如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
【分析】根据∠C=90°AD=AC,求证△CAE≌△DAE,∠CAE=∠DAE=∠CAB,再由∠C=90°,∠B=28°,求出∠CAB的度数,然后即可求出∠AEC的度数.
解:∵在△ABC中,∠C=90°,
AD=AC,DE⊥AB交BC于点E,
∴△CAE≌△DAE,∴∠CAE=∠DAE=∠CAB,
∵∠B+∠CAB=90°,∠B=28°,
∴∠CAB=90°﹣28°=62°,
∵∠AEC=90°﹣∠CAB=90°﹣31°=59°.
故选:B.
8.在△ABC中,∠BAC=90°,AB>AC,∠B≠30°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是( )
A. B.
C. D.
【分析】根据“要在BC边上找一点D,使AD=BD”知点D应该是线段AB垂直平分线与BC的交点,据此求解即可.
解:若要在BC边上找一点D,使AD=BD,
则点D应该是线段AB垂直平分线与BC的交点,
故选:D.
二、填空题(本大题共6小题,每小题3分,共18分)
9.二次根式有意义,则x的取值范围是 x≤3 .
【分析】直接利用二次根式有意义的条件,即二次根式中的被开方数是非负数,进而得出答案.
解:二次根式有意义,则9﹣3x≥0,
故x的取值范围是x≤3.
故答案为:x≤3.
10.比较大小:﹣3 < 0(填“>”、“=”或“<”).
【分析】首先求出介于2和3之间,从而得最后答案.
解:∵2<<3,
∴﹣3<0.
故答案为:<.
11.计算:2x•(﹣3xy)= ﹣6x2y .
【分析】根据单项式乘单项式的运算法则计算.
解:2x•(﹣3xy)=﹣6x2y,
故答案为:﹣6x2y.
12.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 30 .
【分析】先根据勾股定理的逆定理判定三角形是直角三角形,再利用面积公式求得面积.
解:∵52+122=132,
∴三边长分别为5、12、13的三角形构成直角三角形,其中的直角边是5、12,
∴此三角形的面积为×5×12=30.
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,若CD=2,AB=5,则△ABD的面积为 5 .
【分析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,再利用三角形的面积公式列式计算即可得解.
解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD=2,
∴△ABD的面积=AB•DE=×5×2=5.
故答案为:5.
14.如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠DAE=72°,则∠EDC的度数为 33° .
【分析】利用等腰三角形两底角相等和三角形内角和定理可得.
解:∵∠BAD=30°,∠DAE=72°,AB=AC,
∴∠B=∠C==39°,
∵AD=DE,
∴∠DAE=∠DEA=72°,
∵∠AED=∠C+∠EDC,
∴∠EDC=∠AED﹣∠C=72°﹣39°=33°,
故答案为:33°.
三、解答题(本大题共10小题,共78分)
15.计算:﹣﹣﹣|﹣6|.
【分析】直接利用二次根式的性质以及立方根的性质、绝对值的性质分别化简得出答案.
解:原式=4﹣+0.5﹣6
=﹣2.
16.因式分解:
(1)4m2﹣36;
(2)2a2b﹣8ab2+8b3.
【分析】(1)直接提取公因式4,再利用平方差公式分解因式即可;
(2)直接提取公因式2b,再利用完全平方公式分解因式即可.
解:(1)原式=4(m2﹣9)
=4(m+3)(m﹣3);
(2)原式=2b(a2﹣4ab+4b2)
=2b(a﹣2b)2.
17.图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长均为1,点A、点B均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图①中,以线段AB为腰画一个等腰三角形.
(2)在图②中,以线段AB为底画一个等腰三角形.
【分析】(1)根据要求作出图形即可;
(2)根据要求作出图形即可.
解:(1)如图1中,△ABC即为所求;
(2)如图2中,△ABC即为所求.
18.先化简,再求值:(x﹣3)2﹣x(2x+1)+x2,其中x=.
【分析】直接利用乘法公式、单项式乘多项式化简,合并同类项,再把已知数据代入得出答案.
解:原式=x2﹣6x+9﹣2x2﹣x+x2
=﹣7x+9,
当x=时,
原式=﹣7×=﹣1.
19.如图,点B、F、C、E四点在同一条直线上,∠B=∠E,AB=DE,BF=CE.求证:AC=DF.
【分析】根据题意得出BC=EF,即可利用SAS证明△ABC和△DEF,再利用全等三角形的性质即可得解.
【解答】证明:∵BF=CE,
∴BF+FC=CE+FC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF.
20.如图,甲乙两船从港口A同时出发,甲船以16海里/时速度沿北偏东40°方向航行,乙船沿南偏东50°方向航行,3小时后,甲船到达C岛,乙船到达B岛.若C、B两岛相距60海里,问:乙船的航速是多少?
【分析】根据方向角的概念求出∠CAB=90°,根据勾股定理求出AC的长,得到答案.
解:∵甲船沿北偏东40°方向航行,乙船沿南偏东50°方向航行,
∴∠CAB=90°,
∵AB=16×3=48,BC=60,
∴AC==36,
∴乙船的航速是36÷3=12海里/时,
答:乙船的航速是36÷3=12海里/时.
21.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形.
(1)图2中间空白的部分的面积是 (a﹣b)2 ;
(2)观察图2,请你写出代数式(a+b)2、(a﹣b)2、ab之间的等量关系式 (a﹣b)2=(a+b)2﹣4ab ;
(3)根据你得到的关系式解答下列问题:若x+y=﹣4,xy=3,求x﹣y的值.
【分析】(1)由图形面积间和差关系可得此题结果为(a﹣b)2;
(2)由图形面积间关系可得:(a﹣b)2=(a+b)2﹣4ab;
(3)由(2)题关系式可得,(x﹣y)2=(x+y)2﹣4xy,就能求得最后结果.
解:(1)由题意得,图2中间空白的部分的面积是(a﹣b)2,
故答案为:(a﹣b)2;
(2)由图2中间空白的部分的面积的不同表示方法可得:(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(3)由(2)题关系式可得,
(x﹣y)2=(x+y)2﹣4xy=(﹣4)2﹣4×3=4
∴x﹣y=±2,
即x﹣y的值是±2.
22.2021年央视春晚,数十个节目给千家万户送上了丰富的“年夜大餐”.某校随机对八年级部分学生进行了一次调查,对最喜欢相声《年三十的歌》(记为A)、歌曲《牛起来》(记为B)、武术表演《天地英雄》(记为C)、小品《开往春天的幸福》(记为D)的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:
(1)求本次接受调查的学生人数.
(2)求扇形统计图中D所在扇形的圆心角度数.
(3)将条形统计图补充完整.
【分析】(1)根据B的人数除以所占的百分比得到接受调查的学生人数;
(2)用360°乘以D节目男、女生人数和占被调查人数的比例即可;
(3)先求出D所占百分比,再求出C所占百分比,继而可以求出C的人数,进而得出C中男生人数;用总人数乘A占的百分比得出A的人数进而得出A中女生人数,然后补全条形统计图即可;
解:(1)本次接受调查的学生人数为(12+8)÷40%=50(名);
(2)扇形统计图中D所在扇形的圆心角度数为360°×=36°;
(3)D占的百分比为×100%=10%,C占的百分比为1﹣(20%+40%+10%)=30%,
∴C的人数为50×30%=15(人),即C中男生为15﹣8=7(人);A的人数为50×20%=10(人),A中女生人数为10﹣6=4(人),
补全条形统计图,如图所示:
23.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图(1)的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系.
【分析】(1)①根据AD⊥MN,BE⊥MN,∠ACB=90°,得出∠CAD=∠BCE,再根据AAS即可判定△ADC≌△CEB;②根据全等三角形的对应边相等,即可得出CE=AD,CD=BE,进而得到DE=CE+CD=AD+BE;
(2)先根据AD⊥MN,BE⊥MN,得到∠ADC=∠CEB=∠ACB=90°,进而得出∠CAD=∠BCE,再根据AAS即可判定△ADC≌△CEB,进而得到CE=AD,CD=BE,最后得出DE=CE﹣CD=AD﹣BE;
(3)运用(2)中的方法即可得出DE,AD,BE之间的等量关系是:DE=BE﹣AD.
解:(1)①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠ACB=90°=∠CEB,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
②∵△ADC≌△CEB,
∴CE=AD,CD=BE,
∴DE=CE+CD=AD+BE;
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
∴CE=AD,CD=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)当MN旋转到题图(3)的位置时,AD,DE,BE所满足的等量关系是:DE=BE﹣AD.
理由如下:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CE=AD,CD=BE,
∴DE=CD﹣CE=BE﹣AD.
24.如图,在Rt△ABC中,∠ABC=90°,BC=AB,AC=8,点D是边AC的中点,动点P从点D出发,沿DA以每秒2个单位长度的速度向终点A匀速运动.同时,动点Q从点D出发,沿DC以每秒1个单位长度的速度向终点C匀速运动.当点P到达终点时,点Q也随之停止运动.过点Q作QE⊥AC,使QE=QD,且点E落在直线AC的上方,当点P不与点D重合时,以PQ、QE为邻边作长方形PQEF.设长方形PQEF与△ABC的重叠部分的面积为S,点P的运动时间为t(秒).
(1)用含t的代数式表示线段AP的长度为 4﹣2t .
(2)当点F落在线段AB上时,求t的值.
(3)用含t的代数式表示S.
(4)连结AF、DF.当△AFD是等腰三角形时,直接写出t的值.
【分析】(1)由AC=8,点D是边AC的中点求出AD的长为4,再由动点P从点D出发,沿DA以每秒2个单位长度的速度向终点A匀速运动,且运动的时间为t得PD=2t,则AP=4﹣2t;
(2)当点F落在线段AB上时,可证明△APF是等腰直角三角形,则AP=FP=QE=t,可列方程t=4﹣2t,解方程求出t的值即可;
(3)先确定当点P到达终点A时,则点E恰好落在BC边上,再分两种情况进行讨论,一是当0<t≤时,长方形PQEF与△ABC的重叠部分的面积S为长方形PQEF本身,二是当<t≤2时,则长方形PQEF与△ABC的重叠部分的面积S为S长方形PQEF﹣S△FGH,分别求出用含t的代数式表示S的等式即可;
(4)△AFD是等腰三角形存在两种情况,一是AF=DF,则PD=PA=AD=2,列方程求出t的值;二是FD=AD=4,在Rt△PDF中根据勾股定理列方程求出t的值即可.
解:(1)∵AC=8,点D是边AC的中点,
∴AD=AC=4,
∵PD=2t,
∴AP=4﹣2t,
故答案为:4﹣2t.
(2)当点F落在线段AB上时,如图1,
∵四边形PQEF是长方形,
∴∠QPF=90°,FP=QE,
∴∠APF=180°﹣∠QPF=90°,
∵∠ABC=90°,BC=AB,
∴∠A=∠C=45°,
∴∠PFA=∠A=45°,
∴AP=FP=QE,
∵QE=QD=t,
∴AP=t,
∴t=4﹣2t,
解得t=,
∴当点F落在线段AB上时,t的值为.
(3)当点P与点A重合时,则2t=4,
解得t=2,此时QD=QE=QC=2,
∴点E恰好落在BC边上,
当0<t≤时,如图2,
∵PD=2t,QE=QD=t,
∴PQ=2t+t=3t,
∵S=S长方形PQEF=PQ•QE,
∴S=3t•t=3t2;
当<t≤2时,如图3,PF交AB于点G,EF交AB于点H,
∵∠PGA=∠A=45°,
∴∠FGH=∠PGA=45°,
∵∠F=90°,
∴∠FHG=∠FGH=45°,
∴FH=FG,
∵FP=QE=t,GP=AP=4﹣2t,
∴FH=FG=t﹣(4﹣2t)=3t﹣4,
∵S=S长方形PQEF﹣S△FGH,
∴S=3t2﹣(3t﹣4)2=﹣t2+12t﹣8,
综上所述,S=.
(4)如图4,△AFD是等腰三角形,且AF=DF,
∵PF⊥AD,
∴PD=PA=AD=2,
∴2t=2,
解得t=1;
如图5,△AFD是等腰三角形,且FD=AD=4,
∵∠DPF=90°,
∴PD2+FP2=FD2,
∵PD=2t,FP=t,
∴(2t)2+t2=42,
解得t=或t=﹣(不符合题意,舍去),
综上所述,t的值为1或.
2021-2022学年吉林省长春市绿园区八年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年吉林省长春市绿园区八年级(下)期末数学试卷(Word解析版),共20页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
吉林省长春市绿园区2021-2022学年七年级下学期期末考试数学试题(word版含答案): 这是一份吉林省长春市绿园区2021-2022学年七年级下学期期末考试数学试题(word版含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年吉林省长春市绿园区中考二模数学试题(word版含答案): 这是一份2022年吉林省长春市绿园区中考二模数学试题(word版含答案),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












