数学选择性必修 第一册第二章　平面解析几何2.3 圆及其方程2.3.1 圆的标准方程课文内容ppt课件

这是一份数学选择性必修 第一册第二章　平面解析几何2.3 圆及其方程2.3.1 圆的标准方程课文内容ppt课件，共26页。PPT课件主要包含了新知提炼，由题意得，因此圆的标准方程为，课堂小结，圆的标准方程，点与圆的位置关系，点M在C内，点M在C上，点M在C外等内容，欢迎下载使用。

（1）若 ， ，判断点 是否在圆上；
因为， ，所以点A在C上.
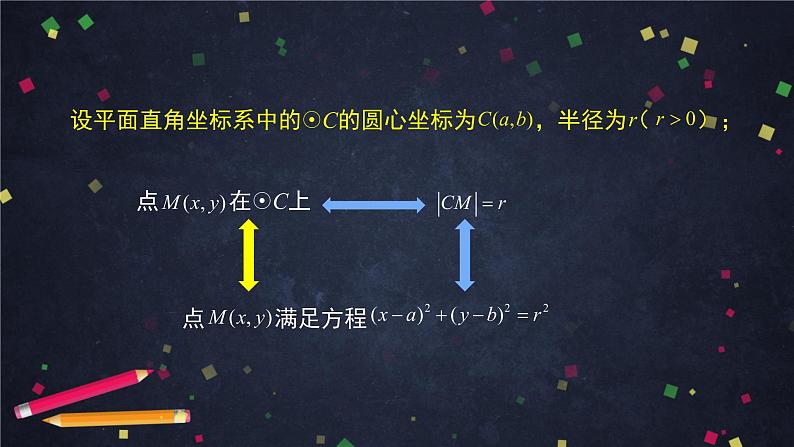
设平面直角坐标系中的C的圆心坐标为 ，半径为（ ）；
（2）若 ， ，设 是平面直角坐标系中任意一点，那么点M在C上的充要条件是什么？
由圆的定义知， 在C上的充要条件是 .
即 ，
也即 .
分析：点M在C上的充要条件是|CM |=2 .
（3）设 是平面直角坐标系中任意一点，那么点M在C上的充要条件是什么？
同理，点 在C上的充要条件是 .
即 ，
也即 .
点 满足方程
点 在C上
一般地，平面直角坐标系中C的圆心为 ，半径为 （ ），称为圆的标准方程.
同直线中一样，我们称圆 时，指的是方程为 的圆.
（4）设 是平面直角坐标系中一点，那么点N与C是什么位置关系？
由圆的定义知， 在C上的充要条件是 , 即 .
同理，点 在C内的充要条件是 , 即 ；
点 在C外的充要条件是 , 即 .
一般地，C的圆心为 ，半径为 （ ），点 ，则 点 在圆内 ； 点 在圆上 ；点 在圆外 .
例1.已知C的标准方程为 .
（1）请写出C的圆心坐标及半径；
解：由圆的标准方程知，圆心 ， ；
解: 因为 ，故点P在C外；
（2）已知 ，试判断点P与C的位置关系；
（3）已知 ，过点P向C作切线，求切线的长度.
解：如图所示，过点P做C的切线l1,l2. 切点分别为Q1,Q2.易知，
解得 ，即切线长为 .
又因为 ，由勾股定理有
例2.根据下列条件，求出圆的标准方程：
（1）圆心在 ，且过点 ；
解：所求圆的半径
圆心是 ，所以圆的标准方程为
即 .
分析：由于圆心坐标未知，不妨先设圆心坐标.
（2）过点 和点 ，半径为 ；
解：设圆心为 ，则圆的标准方程为 .
因为点 和点 在圆上，所以
因此，圆的标准方程为
解：设圆心为 ，半径为 ，圆的标准方程为 .
（3）圆心在直线 上，且过点 .
分析：由于圆过A,B两点，故圆心在线段AB的垂直平分线m上.即圆心C为直线l与直线m的交点.
法2：设线段AB的垂直分线为m，
因此，圆心C满足
线段AB的中点坐标为 .
直线m的方程为 ，即 .
即圆心为 .
法2：圆的半径
故圆的标准方程为
例3.赵州桥位于我国河北省，是我国现存最早、保存最好的巨大石拱桥.如图所示，赵州桥是一座空腹式的圆弧形石拱桥，现测得赵州桥的跨度a和圆拱高b，试用a,b表示出赵州桥圆弧所在圆的半径.
解：作出示意图如图所示，其中AB表示跨度，O为AB中点，OC为拱高，D为圆心.
由垂径定理知， ，故
解得
法2：作出示意图如图所示，其中AB表示跨度，O为AB中点，OC为拱高.以O为点，AB所在直线为 轴建立平面直角坐标系.根据已知有 ， 在圆上，且圆心在 轴上.
设圆心 ，半径为 ，因为B,C都在圆上，所以
解得 .
设C的标准方程为 ，点 ，
圆心为 ，半径为 的圆的标准方程为
3.利用待定系数法与几何法求圆的标准方程
1.已知点 ，和C : ；（1）请写出C的圆心坐标与半径；（2）判断点P与的位置关系；（3）过点P作C的切线，求切线的长度.
2.根据下列条件，求出圆的标准方程：（1）圆心坐标为原点，半径为 ；（2）圆心为 ，半径为 ；（3）经过点 ，且圆心在直线 上. 上